文章来源：Optimal Transport的前世今生 | (一) 从Monge问题到Kantorovich问题 (opens new window) 仓库：Awesome Optimal Transport in Deep Learning (opens new window)

1. OT发展时间线

Optimal Transport (OT) 最优传输是什么？一句话概括：OT问题是一个优化问题，它的目标是优化出两个分布之间传输的最小代价解。

近几年OT受到广泛关注，在各大ML/CV/NLP顶会中都能看到它的影子，CVPR 2023更是接收了5篇用OT处理CV任务的文章。为了让大家能够了解OT是怎么一步步火起来的，在时代的浪潮中捕捉一些sense，以下将分别总结OT理论和OT与深度学习相结合应用的发展时间线。

1.1 OT理论发展时间线

• 1781年，法国数学家Gaspard Monge首次提出了最优运输问题的形式化描述，他研究了将一个土堆重新排列成另一个土堆的最佳方法，这个问题被称为Monge问题。
• 1942年，前苏联数学家Leonid Kantorovich重新形式化了Monge的问题，这个问题被称为Kantorovich问题，并提出了一种线性规划方法来解决它。Kantorovich问题源自于他在第二次世界大战前后所面临的实际问题，在资源分配问题中发挥了重要作用。因为他的理论最初在经济领域（但当然不仅限于此）的应用，Kantorovich于1975年获得诺贝尔经济学奖。
• 1991年，法国数学家Yann Brenier首次证明了连续形式Monge和Kantortich问题的等价性。对连续分布问题传输的研究，使得定义任何概率测量之间的传输问题成为可能，推动了OT的发展。
• 先前开创性的工作展示了运输问题和偏微分方程之间的联系。菲尔兹奖得主Cédric Villani（2010）和Alessio Figalli（2018）均深耕于该方向。
• 2013年，Marco Cuturi提出了熵正则化的OT问题，并提出轻量级的OT求解器Sinkhorn算法，大幅提升了OT的求解速度。往后大多需要求解匹配矩阵的工作，都基于熵正则化的OT问题，使用Sinkhorn算法高效求解。

1.2 近期OT与深度学习相结合应用的发展时间线

• 2016年前后，恰逢当时深度学习刚起步，以Nicolas Courty为代表的学者们开始把OT引入Domain Adaptation (DA) 领域，基于sample-to-sample的匹配思想匹配源域和目标域样本，并用深度神经网络训练取得了不错的效果。随后，OT在DA领域受到了广泛关注，涌现出许多工作基于此思想对任务进行建模。
• 2017年，正值GAN大热潮，Wasserstein GAN#ref_1被提出，使得OT在深度学习社区中小火了一把，受到了广泛的“出圈”讨论，大幅提升了OT的知名度。
• 2020年，自监督学习大热，Self-labeling#ref_2和SwAV#ref_3提出基于OT的伪标签标记方法，基于sample-to-prototype的匹配思想解决聚类问题。后来FAIR的SwAV受到广泛的关注，也成了几篇经典自监督巨头之作之一，OT-based伪标签标记方法开始大热，各大顶会开始频繁出现类似思想的工作。

2. Monge问题

需要注意的是，本文将主要以离散形式对Monge问题和Kantorovich问题进行定义和讨论，对连续形式感兴趣的朋友可以参阅Cuturi的书#ref_4。

2.1 问题引入：一个简单的“烘焙房-咖啡厅”供需运输问题

为了方便读者更好理解，我将简单地定义一个简化的“烘焙房-咖啡厅”供需运输问题，让大家对基于Monge问题的OT问题有一些大概的感知。

假设有6家烘焙房每天为6家咖啡厅提供面包配送服务。每家烘焙房和咖啡厅分散在城市的不同位置，每家烘焙房 $x_i$ 到每家咖啡厅 $y_i$ 的送货时间 $C_{i,j}$ 也不同，如图1（左）所示。
需要注意的是，我们这里规定一家烘焙房只能为一家咖啡厅提供服务，即一对一匹配。因此我们这里简单假设：烘焙房的供应量等于每家咖啡厅的需求量，即每家店的供应量和需求量都是一致的。我们需要定义一个优化问题，在满足上述条件的同时，求解出整体送货时间最短的配送方案。

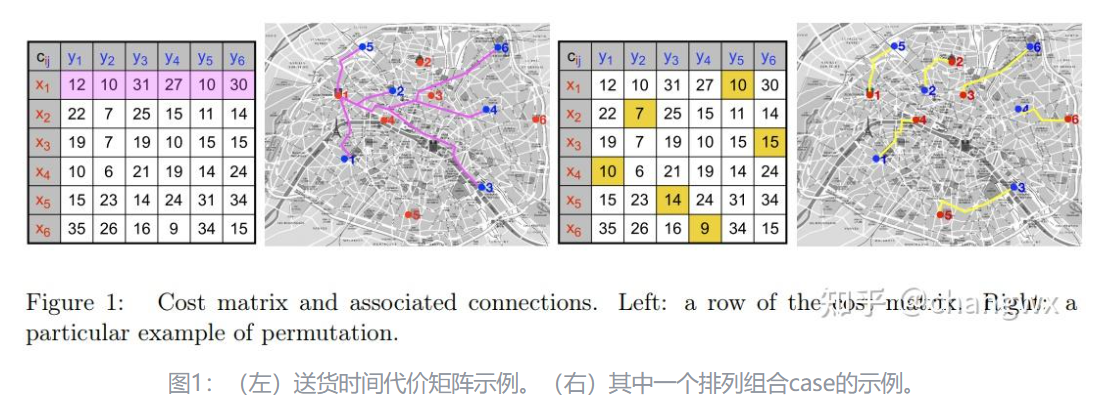
考虑到“一对一匹配”的限制，因此运送方案就是“烘焙房-咖啡厅”的组合问题。一共有 $A_6^6=6!$ 种组合方案，我们可以用 ${\mathrm{\Sigma }}_6$ 来表示所有可能的组合方案集合。

另外我们这里定义 $\sigma$ 来表示从烘焙房 $\{x_1,\cdots ,x_6\}$ 到咖啡厅 $\{y_1,\cdots ,y_6\}$ 的映射：

$$\begin{array}{}\text{(1)}& \sigma :i\in \{1,\cdots ,6\}\mapsto j\in \{1,\cdots ,6\},\end{array}$$

即 $\sigma (i)=j$ 表示烘焙房 $x_i$ 的货物将送到咖啡厅 $y_j$。

待求解的“烘焙房-咖啡厅”最短时间配送方案，其实就是通过最小化以下优化问题，从而得到最优的运输方案（coupling matrix） ${\sigma }^{\ast }$ ：

$$\begin{array}{}\text{(2)}& {\sigma }^{\ast }=\underset{\sigma \in {\mathrm{\Sigma }}_6}{\arg \min }\sum _{i=1}^6{C}_{i,\sigma (i)}.\end{array}$$

2.2 离散形式的Monge问题

在现实运输问题中，并不是每家的烘焙房和咖啡厅的供应量和需求量都相等，也不是烘焙房和咖啡厅的数量都一样，因此这里给出更加泛化的问题定义。

假设有 $n$ 家烘焙房每天为 $m$ 家咖啡厅提供面包配送服务。每家烘焙房和咖啡厅分散在城市的不同位置，每家烘焙房 $x_i$ 到每家咖啡厅 $y_i$ 的送货时间 $C_{i,j}$ 也不同。规定一家烘焙房只能为一家咖啡厅提供服务。

所有供应量和需求量可以用离散分布表示，因此供方分布向量 $\alpha$ 和需方分布向量 $\beta$ 可以表示如下：

$$\begin{array}{}\text{(3)}& \alpha =\sum _{i=1}^n{a}_i{\delta }_{x_i}\text{and}\beta =\sum _{j=1}^m{b}_j{\delta }_{y_j}\end{array}$$

其中 $a_i$ 表示烘焙房 $x_i$ 的供应量， $b_j$ 表示咖啡厅 $y_j$ 的需求量， ${\delta }_x$ 是在点 $x$ 处的狄拉克函数。另外需要补充一个OT中常用的概念：mass，直觉理解就是“一个土堆”，比如 $a_i{\delta }_{x_i}$ 就是一个mass。

Monge问题目标是寻找一个运输代价最小的映射 $T:\{x_1,\cdots ,x_n\}\mapsto \{y_1,\cdots ,y_n\}$ ，将一个分布中的“小土堆”mass运输到另一个分布中，并且 $T$ 必须要满足

$$\begin{array}{}\text{(4)}& \mathrm{\forall }j\in \{1,\cdots ,m\},b_j=\sum _{i:T(x_i)=y_j}{a}_i，\end{array}$$

这个约束条件可以被紧密地表示为 $T_{\mathrm{\#}}\alpha =\beta$ ，被称作mass conservation constraint。 $T_{\mathrm{\#}}$ 也被称作push-forward操作。

这里需要特别解释一下mass conservation constraint：当 $n=m$ 时push-forward操作可以实现“1x $\leftrightarrow$ 1y”的映射关系（图2左）；当 $n>m$ 则意味着 “1x $\to$ 1y, 1y $\leftarrow$ 多x”的映射关系（图2右），即一个 $x_i$ 只能输出到一个 $y_j$ ，但是一个 $y_j$ 许输入多个 $x_i$；当 $n<m$ 则意味着该优化问题无解。

Monge问题的形式化表达如下：

$$\begin{array}{}\text{(5)}& \underset{T}{min}\{\sum _{i=1}^{n}c(x_i,T(x_i)):T_{\mathrm{\#}}\alpha =\beta \},\end{array}$$

其中 $c(x_i,T(x_i))$ 表示从 $x_i$ 到 $T(x_i)$ 的代价分数。

可以观察到，我们在2.1所定义的简单“烘焙房-咖啡厅”的供需运输问题其实是Monge问题的一个特殊case，即 $n=m$ , $\alpha =\beta =\frac{1}{n}{\mathbf{1}}_n$ ，如图2（左）所示。

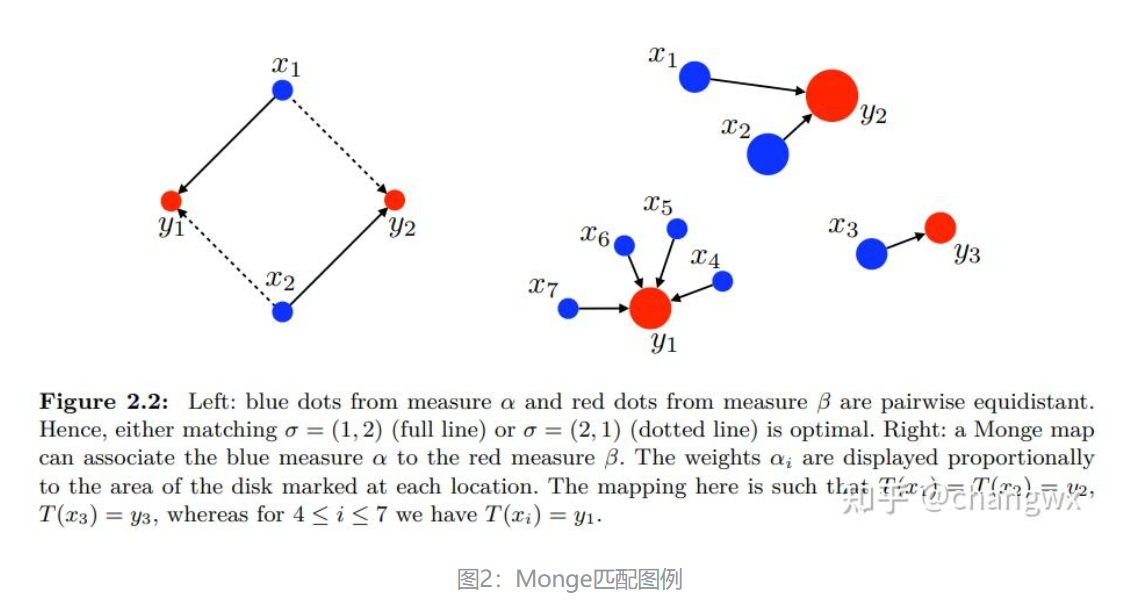
2.3 Monge问题的缺点

对于任意两个分布不一定存在可行解

当 $n\ne m$ 时，Monge问题不一定存在满足约束(4)的可行解。比如图2（右）所示，$\alpha \mapsto \beta$ 存在可行最优解，但是 $\beta \mapsto \alpha$ 并不存在可行解（此时 $n<m$ ，供小于求）。

可行域非凸，求解效率低下

另外，问题(5)的可行域是非凸的，这是由约束(4)中定义的mass conservation constraint导致的，即push-forward操作将导致优化问题求解非常棘手。即使是在2.1中定义的简化问题，也需要通过穷举 $A_6^6=6!$ 种组合方案来求解，这种求解方法随着 $n$ 规模的增长将导致灾难级的时间复杂度，比如 $70!\approx 1.198\times {10}^{100}$ ，这是我们不能接受的。

总结一下，Monge问题无法无限制地应用于各种分布运输问题，主要是受限于约束(4)中定义的mass conservation constraint。

既然都是push-forward操作的锅，能不能把它改一下，使整个OT问题变成凸问题呢？这样即保证了唯一的可行解，又可以灵活地使用各种优化方法求解全局最优解。前苏联数学家Leonid Kantorovich就做了这么一件事，提出了Kantorovich问题。往后的OT问题，大家都倾向于默认使用Kantorovich问题的定义。接下来让我们来了解一下Kantorovich问题。

3. Kantorovich问题

约束(4)中定义的mass conservation constraint本质上就是一种“1x$\to$1y, 1y $\leftarrow$ 多x”匹配（图2右）的限制，是否可以不强制要求供应方只能单独服务一个需求方呢？即“多x $\leftrightarrow$ 多y”匹配。

3.1 Kantorovich问题的定义

下面我们直接给出Kantorovich问题的定义。

给定一个代价矩阵 $\mathbf{C}\in {\mathbb{R}}^{n\times m}$ , 离散概率分布向量 $\alpha \in {\mathbb{R}}^n$ 和 $\beta \in {\mathbb{R}}^m$ ， 求解从 $\alpha$ 分布到 $\beta$ 分布映射的最小代价匹配矩阵 $P^{\ast }$ 可以被量化成以下优化问题：

$$\begin{array}{}\text{(6)}& \underset{P\in U(\alpha ,\beta )}{min}⟨C,P⟩\stackrel{\underset{\mathrm{def}}{}}{=}\sum _{i,j}{C}_{i,j}{P}_{i,j},\end{array}$$$$\begin{array}{}\text{(7)}& U(\alpha ,\beta )=\{P\in {\mathbb{R}}_{+}^{n\times m}|P{\mathbf{1}}_m=\alpha ,P^{\mathrm{\top }}{\mathbf{1}}_n=\beta \},\end{array}$$

其中， $U(\alpha ,\beta )$ 经常被称为polytope。

该如何理解Kantorovich问题的数学表达呢？ 主要有以下四点：

1. $C$ 和 $P$ 的矩阵内积应尽可能地小，即运输代价越小的两个传输点之间应该获得更大的匹配权重 $P_{i,j}$ ；
2. Kantorovich问题中松弛了**“1x**$\to$1y, 1y $\leftarrow$ 多x”匹配（图2右），允许了“多x $\leftrightarrow$ 多y”匹配，如图3(c)所示;
3. $P^{\ast }$ 的行和等于 $\alpha$ 向量，列和等于 $\beta$ 向量，即供应方输出的货量总和等于货物持有量、需求方输入的货量总和等于需求期望量，如图3(a)所示；
4. 基于第2点，考虑到矩阵 $P^{\ast }$ 的行和列和分别等于两个概率分布向量，因此 $P^{\ast }$ 也可以被理解为联合概率分布矩阵， $\alpha$ 和 $\beta$ 也常被称为“边缘概率分布向量”，如图3(b)所示。

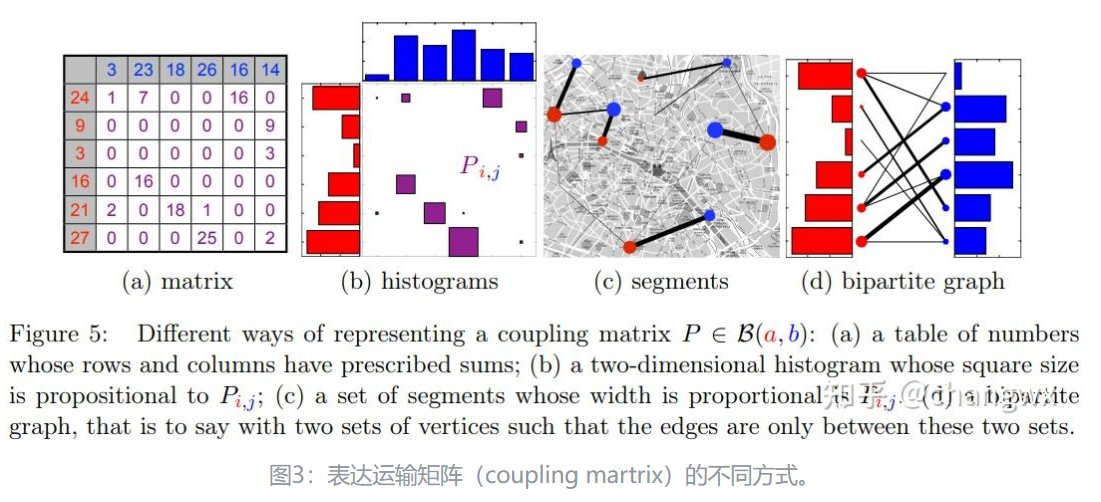
3.2 Monge与Kantorovich问题的对比

相较于Monge问题(5)，Kantorovich问题的形式改变有以下理解：

• 从动机角度来说，Kantorovich问题松弛了Monge问题中的mass conservation constraint，引入mass splitting思想，即源点 $x_i$ 可以被分散地运输到不同地方（允许一家烘焙店供应多家咖啡厅）；
• 从思想角度来说，Kantorovich问题松弛了Monge问题中的确定性运输（deterministic transport），转而考虑概率运输（probabilistic transport）；
• 从可解性角度来说，相比于Monge问题不一定存在可行解，Kantorovich问题是一个明确的凸问题，必然存在唯一最优解；
• 从求解角度来说，相比于非凸的Monge问题，Kantorovich问题是一个线性规划问题，可以调用现成线性规划求解器，极大地提高了求解速度；
• 从泛化性角度来说，相比于Monge问题局限的应用场景（矩阵规模极小、特定的分布输入），Kantorovich问题可以更灵活地应用于任意两个概率分布，极大地扩大了OT的应用场景。

4. OT的应用举例

4.1 Monge问题的应用：Color transfer问题

在Color transfer问题中，我们有一副塞尚的画作（图4左），一副毕加索的画作（图4中），目标是把毕加索的画作颜色风格迁移到塞尚的画作中去（图4右）。

现只需要简单的分别定义 $x_i,y_j\in {\mathbb{R}}^3$ 为两张图片的RGB值，定义代价矩阵为 $C_{i,j}={\Vert x_i-y_j\Vert }^2$ （欧氏距离），然后代入Monge问题(5)求解 $\sigma$ 。最后所得图片（图4右）用 $y_{\sigma (i)}$ 表示，它表示塞尚的画作的第 $i$ 个像素点 $x_i$ 匹配到毕加索的画作中第 $\sigma (i)$ 个像素点 $y_{\sigma (i)}$ 的RGB值。

4.2 Kantorovich问题的应用：3D物件插值

从某种程度来说，Kantorovich问题(6)的优化目标最优值可以看做是一种类似于KL散度的分布度量，它衡量了两个分布的距离，我们可以简单表示成 $W(\alpha ,\beta )\stackrel{\underset{\mathrm{def}}{}}{=}\sum _{i,j}{C}_{i,j}{P}_{i,j}^{\ast }$ ，其中代价矩阵可以用欧式距离定义为$C_{i,j}={\Vert x_i-y_j\Vert }^2$ 。

3D物件插值任务的目标是，给 $n$ 个3D物件，输入权重向量 $\{w_1,\cdots ,w_n\}$ ，其中 $\sum _k^n{w}_k=1$ ，输出给定物件间的加权插值3D物件。如图5所示，三角形排列的三个顶点分别是3个提前给定的3D物件，再给定不同的对应权重向量，可以在3个物体间生成不同的加权插值3D物件。

我们以图5中的三个物件为例，分别给定三个物件对应的分布 $(\alpha ,\beta ,\gamma )$ ，只需要定义3D物体内为均匀分布、物体外分布是0即可。另外还需给定三个物件的对应的权重 $(w_1,w_2,w_3)$ 。求解加权插值3D物件其实就是求解关于 $(\alpha ,\beta ,\gamma )$ 的加权质心（weighted barycenter） $\mu$ 。因此可以定义以下优化问题：

$$\begin{array}{}\text{(8)}& {\mu }^{\ast }=\underset{\mu }{\arg \min }{w}_{1}W(\alpha ,\mu )+w_{2}W(\beta ,\mu )+w_{3}W(\gamma ,\mu ).\end{array}$$

通过求解得到的 ${\mu }^{\ast }$ 即可重构出目标的插值3D物件。

5. 小结

本文梳理了OT的发展历史，尤其对Monge问题和Kantorovich问题进行了深入的介绍，并给出了一些应用举例，希望能为大家的OT学习带来一些帮助。

以下是一些本系列专栏的预告:)

在3D物件插值的case中，我们提到OT的优化目标最优值可以看做是一种类似于KL散度的分布度量，这也就是大名鼎鼎的Wasserstein距离（也被称之为推土机距离），并且在GAN中有一个大热的应用Wasserstein GAN，通过理论证明了Wasserstein距离对比KL散度、JS散度在度量分布距离中的优势。接下来我也会在本系列专栏《Optimal Transport的前世今生》的第二篇文章进行剖析，欢迎感兴趣的朋友关注~

另外，虽然相比于Monge问题，Kantorovich问题作为线性规划问题有极大的求解优势。但是在深度学习蓬勃发展的当下，大规模矩阵的OT求解问题依旧棘手（内点法 $O(n^3\log (n))$ ）。直到后来熵正则化+Sinkhorn算法被提出。如此一个轻量级的OT求解器才促成了OT在深度学习时代被大规模地应用，这也是OT中非常重要的求解器。我计划将在本系列专栏的第三篇文章中进行详细解读，跟其他解读文章不一样的是，我将从KL投影角度理解熵正则化项，这一定会帮助你对Sinkhorn算法求解的理解迈上一个新的台阶！ 欢迎感兴趣的朋友关注~

6. 补充资料

1. Numerical Optimal Transport and its Applications https://mathematical-tours.github.io/book-basics-sources/ot-sources/TransportEN.pdf (opens new window)
2. Computational Optimal Transport https://arxiv.org/abs/1803.00567 (opens new window)
3. [Marco Cuturi] A Primer on Optimal Transport https://www.youtube.com/watch?v=6iR1E6t1MMQ (opens new window) https://www.youtube.com/watch?v=1ZiP_7kmIoc&t=377s (opens new window) https://www.dropbox.com/s/3kuqnhmf2q0dzjq/mlss18_argentina.pdf?dl=0 (opens new window)
4. Introduction to Optimal Transport https://www.damtp.cam.ac.uk/research/cia/files/teaching/Optimal_Transport_Notes.pdf (opens new window)
5. Monge and Kantorovich problems: from primal to dual https://lchizat.github.io/files2020ot/lecture1.pdf (opens new window)

参考

• 最优传输 (Optimal transport) 和 sinkhorn 迭代 (opens new window)