大模型精度：FP32、TF32、FP16、BF16、FP8、FP4、NF4、INT8 (opens new window)

大模型的训练和推理，经常涉及到精度的概念，种类很多，而且同等精度级别下，还分不同格式。比如：

浮点数精度 (opens new window)：双精度（FP64）、单精度（FP32、TF32）、半精度（FP16、BF16）、8位精度（FP8）、4位精度（FP4、NF4）

量化精度 (opens new window)：INT8、INT4 （也有INT3/INT5/INT6的）

另外，实际使用场景中，还有多精度和混合精度的概念

什么是精度

假设你每秒钟赚到的钱是1块钱，那一个月的收入是1*60*60*24*30=216000，如果每秒钟赚到1块1呢，那一个月的收入是237600，就一个1毛钱的小数点，让你月收入少了1万多，这就是精度不同导致的差异。

另外一个典型的例子是π，常用3.14表示，但是如果要更高精度，小数点后面可以有无数位。

当然，这些都是数学里面的精度概念，在计算机里面，浮点数的精度，跟存储方式有关，占用的bit越多，精度越高。

为什么要有这么多精度

因为成本和准确度。

都知道精度高肯定更准确，但是也会带来更高的计算和存储成本。较低的精度会降低计算精度，但可以提高计算效率和性能。所以多种不同精度，可以让你在不同情况下选择最适合的一种。

双精度比单精度表达的更精确，但是存储占用多一倍，计算耗时也更高，如果单精度足够，就没必要双精度。

不同的浮点数精度

在计算机中，浮点数存储方式，由符号位（sign）、指数位（exponent）和小数位（fraction）三部分组成。符号位都是1位，指数位影响浮点数范围，小数位影响精度。

FP精度

Floating Point，是最原始的，IEEE定义的标准浮点数类型。由符号位（sign）、指数位（exponent）和小数位（fraction）三部分组成。

FP64，是64位浮点数，由1位符号位，11位指数位和52位小数位组成。

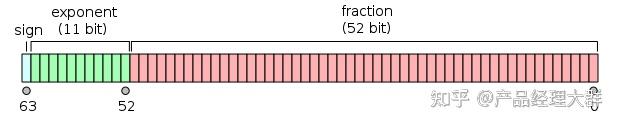
FP32、FP16、FP8、FP4都是类似组成，只是指数位和小数位不一样。但是FP8和FP4不是IEEE的标准格式。

FP8是2022年9月由多家芯片厂商定义的，论文地址：https://arxiv.org/abs/2209.05433 (opens new window)

FP4是2023年10月由某学术机构定义，论文地址：https://arxiv.org/abs/2310.16836 (opens new window)

FP8格式有两种变体，E4M3(4位指数和3位尾数)和E5M2(5位指数和2位尾数)

符号位、指数位、小数位的位数如下表所示：

格式	符号位	指数位	小数位	总位数
FP64	1	11	52	64
FP32	1	8	23	32
FP16	1	5	10	16
FP8 E4M3	1	4	3	8
FP8 E5M2	1	5	2	8
FP4	1	2	1	4

特殊精度

TF32，Tensor Float 32，英伟达针对机器学习设计的一种特殊的数值类型，用于替代FP32。首次在A100 GPU中支持。

由1个符号位，8位指数位（对齐FP32）和10位小数位（对齐FP16）组成，实际只有19位。在性能、范围和精度上实现了平衡。

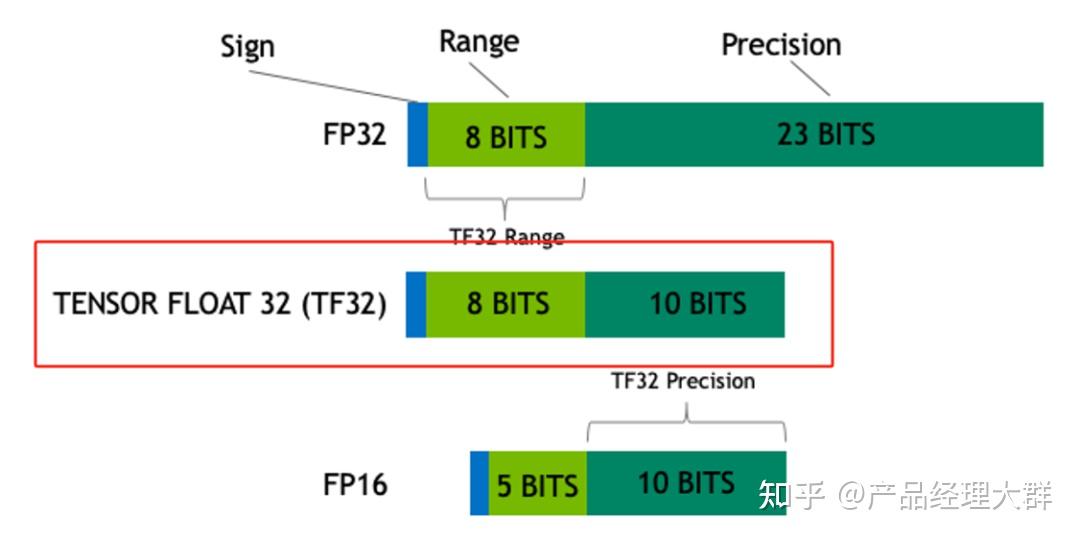
python中查看是否支持：

import torch
//是否支持tf32
torch.backends.cuda.matmul.allow_tf32
//是否允许tf32，在PyTorch1.12及更高版本中默认为False
torch.backends.cudnn.allow_tf32

BF16，Brain Float 16，由Google Brain提出，也是为了机器学习而设计。由1个符号位，8位指数位（和FP32一致）和7位小数位（低于FP16）组成。所以精度低于FP16，但是表示范围和FP32一致，和FP32之间很容易转换。

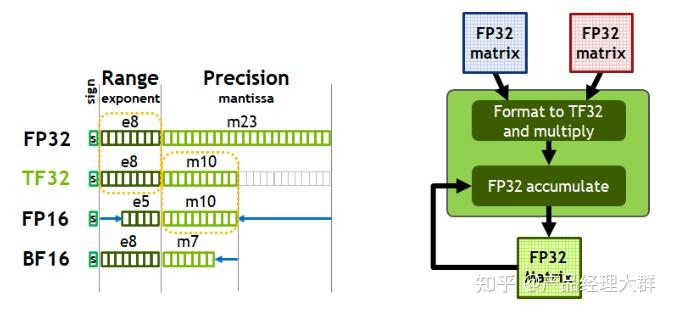
在 NVIDIA GPU 上，只有 Ampere 架构以及之后的GPU 才支持。

python中查看是否支持：

import transformers
transformers.utils.import_utils.is_torch_bf16_gpu_available()

NF4，4-bit NormalFloat，一种用于量化的特殊格式，在QLoRA量化论文中提出。

NF4是建立在分位数量化技术的基础之上的一种信息理论上最优的数据类型。把4位的数字归一化到均值为 0，标准差为 [-1,1] 的正态分布的固定期望值上，知道量化原理的应该就会理解。

FP精度和特殊精度加上，位数总结如下表

格式	符号位	指数位	小数位	总位数
FP64	1	11	52	64
FP32	1	8	23	32
TF32	1	8	10	19
BF16	1	8	7	16
FP16	1	5	10	16
FP8 E4M3	1	4	3	8
FP8 E5M2	1	5	2	8
FP4	1	2	1	4

多精度和混合精度

多精度计算 (opens new window)，是指用不同精度进行计算，在需要使用高精度计算的部分使用双精度，其他部分使用半精度或单精度计算。

混合精度计算 (opens new window)，是在单个操作中使用不同的精度级别，从而在不牺牲精度的情况下实现计算效率，减少运行所需的内存、时间和功耗

量化精度

一般情况下，精度越低，模型尺寸和推理内存占用越少，为了尽可能的减少资源占用，量化算法被发明。FP32占用4个字节，量化为8位，只需要1个字节。

常用的是INT8和INT4，也有其他量化格式（6位、5位甚至3位）。虽然资源占用减少，但是推理结果差不了多少。

量化算法

以下是一些常见的大模型量化算法，这些算法主要用于减少模型的存储和计算需求，同时尽量保持模型的性能

1 权重量化Weight Quantization

• 原理：将模型的权重从浮点数（如32位浮点数）量化为低位宽的表示（如8位、4位或更低）。

• 方法：

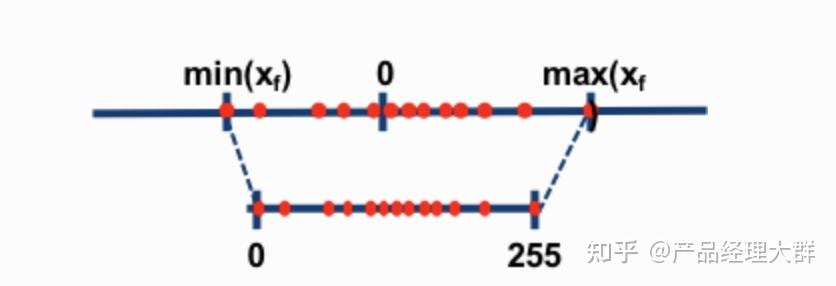
• 线性量化：将浮点数映射到整数区间，例如将[-1, 1]映射到[0, 255]。

• 非线性量化：使用非线性函数（如对数映射）进行量化。

• 均匀量化：在量化区间内均匀分布量化点。

• 非均匀量化：在量化区间内非均匀分布量化点，以更好地捕捉权重分布。

2 激活量化 Activation Quantization

• 原理：将模型的激活值（中间层的输出）从浮点数量化为低位宽的表示。

• 方法：

• 动态量化：在推理过程中动态地量化激活值。

• 静态量化：在模型训练完成后，对激活值进行离线量化。

3 混合精度量化 Mixed-Precision Quantization

• 原理：结合不同精度的表示（如16位浮点数和8位整数），在不同的层或操作中使用不同的量化精度。

• 方法：

• 自适应混合精度：根据模型的性能和精度需求，动态调整不同层的量化精度。

• 手动混合精度：由开发者手动指定哪些层使用哪种精度。

4 知识蒸馏 Knowledge Distillation

• 原理：通过训练一个较小的“学生”模型来模仿一个较大的“教师”模型的行为，从而在量化过程中保持模型性能。

• 方法：

• 软目标蒸馏：使用教师模型的输出作为学生模型的软目标。

• 特征蒸馏：将教师模型的中间层特征传递给学生模型，以保持特征的相似性。

5 量化感知训练 Quantization-Aware Training, QAT

• 原理：在模型训练阶段引入量化操作，使得模型在训练过程中就适应量化带来的变化。

• 方法：

• 模拟量化：在训练过程中，通过模拟量化操作来训练模型。

• 伪量化：在训练过程中，使用伪量化操作来近似量化效果。

6 稀疏量化 Sparse Quantization

• 原理：通过引入稀疏性（如权重稀疏化），减少模型的存储需求和计算复杂度。

• 方法：

• 权重剪枝：将模型中不重要的权重设置为零。

• 稀疏量化：在量化过程中，优先保留重要的权重，忽略不重要的权重。

7 二值化 Binary Quantization

• 原理：将权重和激活值量化为二值（如+1和-1）。

• 方法：

• 二值权重网络（Binary Weight Network, BWN）：仅将权重量化为二值。

• 二值激活网络（Binary Activation Network, BAN）：仅将激活值量化为二值。

• 全二值网络（XNOR-Net）：同时将权重和激活值量化为二值。

8 三值量化 Ternary Quantization

• 原理：将权重和激活值量化为三个值（如-1、0、+1）。

• 方法：

• 三值权重网络（Ternary Weight Network, TWN）：仅将权重量化为三值。

• 三值激活网络（Ternary Activation Network, TAN）：仅将激活值量化为三值。

9 结构化量化 Structured Quantization

• 原理：在量化过程中，保留某些结构化特征（如通道、块等），以提高量化后的性能。

• 方法：

• 通道量化：按通道进行量化，保留通道间的相关性。

• 块量化：按块进行量化，保留块内的相关性。

10 自适应量化 Adaptive Quantization

• 原理：根据数据的分布动态调整量化参数，以更好地适应不同输入数据。

• 方法：

• 动态范围量化：根据输入数据的动态范围调整量化参数。

• 自适应位宽量化：根据数据的重要性动态调整量化位宽。

这些量化算法在实际应用中可以根据模型的具体需求和硬件环境进行选择和组合，以实现最佳的性能和效率平衡。