激活函数

激活函数（Activation Function）是一种添加到人工神经网络中的函数，旨在帮助网络学习数据中的复杂模式。类似于人类大脑中基于神经元的模型，激活函数最终决定了要发射给下一个神经元的内容。

Sigmoid 函数

a = σ (z) = \frac{1}{{1 + e}^{- z}}

应用场景：

Sigmoid 函数的输出范围是 0 到 1。由于输出值限定在 0 到 1，因此它对每个神经元的输出进行了归一化；
用于将预测概率作为输出的模型。由于概率的取值范围是 0 到 1，因此 Sigmoid 函数非常合适；
梯度平滑，避免「跳跃」的输出值；
函数是可微的。这意味着可以找到任意两个点的 sigmoid 曲线的斜率；
明确的预测，即非常接近 1 或 0。

缺点：

倾向于梯度消失；
函数输出不是以 0 为中心的，这会降低权重更新的效率；
Sigmoid 函数执行指数运算，计算机运行得较慢。

tanh函数或者双曲正切函数是总体上都优于sigmoid函数的激活函数。

Tanh 函数

如图， $a = t a n h (z)$ 的值域是位于+1 和-1 之间。

f (x) = t a n h (x) = \frac{e^{x} - e^{- x}}{e^{x} + e^{- x}} = \frac{2}{1 + e^{- 2 x}} - 1 f^{'} (x) = 1 - t a n h^{2} (x)

事实上，tanh函数是sigmoid的向下平移和伸缩后的结果。对它进行了变形后，穿过了 $(0, 0)$ ，并且值域介于+1 和-1 之间。效果优于sigmoid函数。因为函数值域在-1 和+1 的激活函数，其均值是更接近零均值的。在训练一个算法模型时，如果使用tanh函数代替sigmoid函数中心化数据，使得数据的平均值更接近 0 而不是 0.5.

首先，当输入较大或较小时，输出几乎是平滑的并且梯度较小，这不利于权重更新。二者的区别在于输出间隔，tanh 的输出间隔为 1，并且整个函数以 0 为中心，比 sigmoid 函数更好；
在 tanh 图中，负输入将被强映射为负，而零输入被映射为接近零。

注意：在一般的二元分类问题中，tanh 函数用于隐藏层，而 sigmoid 函数用于输出层，但这并不是固定的，需要根据特定问题进行调整。

sigmoid函数和tanh函数两者共同的缺点是，在 $z$ 特别大或者特别小的情况下，导数的梯度或者函数的斜率会变得特别小，最后就会接近于 0，导致降低梯度下降的速度。

ReLu 函数

$$ \sigma(x)=\begin{cases}max(0,x),&x\geq0\\0,&x<0 \end{cases} $$ ReLU 函数是深度学习中较为流行的一种激活函数，相比于 sigmoid 函数和 tanh 函数，它具有如下优点：

当输入为正时，不存在梯度饱和问题。
计算速度快得多。ReLU 函数中只存在线性关系，因此它的计算速度比 sigmoid 和 tanh 更快。

当然，它也有缺点：

Dead ReLU 问题。当输入为负时，ReLU 完全失效，在正向传播过程中，这不是问题。有些区域很敏感，有些则不敏感。但是在反向传播过程中，如果输入负数，则梯度将完全为零，sigmoid 函数和 tanh 函数也具有相同的问题；
我们发现 ReLU 函数的输出为 0 或正数，这意味着 ReLU 函数不是以 0 为中心的函数。

LeakyReLU 函数

它是一种专门设计用于解决 Dead ReLU 问题的激活函数

$$ f(y_i)=\begin{cases}y_i,&y_i>0\\\alpha_iy_i,&y_i\le0 \end{cases} $$

Leaky ReLU 通过把 x 的非常小的线性分量给予负输入（0.01x）来调整负值的零梯度（zero gradients）问题；
leak 有助于扩大 ReLU 函数的范围，通常 a 的值为 0.01 左右；
Leaky ReLU 的函数范围是（负无穷到正无穷）。

注意：从理论上讲，Leaky ReLU 具有 ReLU 的所有优点，而且 Dead ReLU 不会有任何问题，但在实际操作中，尚未完全证明 Leaky ReLU 总是比 ReLU 更好。

ELU 函数

ELU 的提出也解决了 ReLU 的问题。与 ReLU 相比，ELU 有负值，这会使激活的平均值接近零。均值激活接近于零可以使学习更快，因为它们使梯度更接近自然梯度。

g (x) = E L U (x) = {\begin{cases} x, & x > 0 \\ α (e^{x} - 1), & x \leq 0 \end{cases}

显然，ELU 具有 ReLU 的所有优点，并且：

没有 Dead ReLU 问题，输出的平均值接近 0，以 0 为中心；
ELU 通过减少偏置偏移的影响，使正常梯度更接近于单位自然梯度，从而使均值向零加速学习；
ELU 在较小的输入下会饱和至负值，从而减少前向传播的变异和信息。

一个小问题是它的计算强度更高。与 Leaky ReLU 类似，尽管理论上比 ReLU 要好，但目前在实践中没有充分的证据表明 ELU 总是比 ReLU 好。

PReLU(Parametric ReLU)

$$ f(y_i)=\begin{cases}y_i,&y_i>0\\\alpha_iy_i,&y_i\le0 \end{cases} $$ 看一下 PReLU 的公式：参数α通常为 0 到 1 之间的数字，并且通常相对较小。

如果 $α_{i} = 0$ ，则 f 变为 ReLU
如果 $α_{i} > 0$ ，则 f 变为 leaky ReLU
如果 $α_{i}$ 可学习的参数，则 f 变为 PReLU

PReLU 的优点如下：

在负值域，PReLU 的斜率较小，这也可以避免 Dead ReLU 问题。
与 ELU 相比，PReLU 在负值域是线性运算。尽管斜率很小，但不会趋于 0。

这有一些选择激活函数的经验法则：

如果输出是 0、1 值（二分类问题），则输出层选择sigmoid函数，然后其它的所有单元都选择Relu函数。

这是很多激活函数的默认选择，如果在隐藏层上不确定使用哪个激活函数，那么通常会使用Relu激活函数。有时，也会使用tanh激活函数，但Relu的一个优点是：当 $z$ 负值的时候，导数等于 0。

这里也有另一个版本的Relu被称为Leaky Relu。

当 $z$ 负值时，这个函数的值不是等于 0，而是轻微的倾斜，如图。

这个函数通常比Relu激活函数效果要好，尽管在实际中Leaky ReLu使用的并不多。

两者的优点是：

第一，在 $z$ 区间变动很大的情况下，激活函数的导数或者激活函数的斜率都会远大于 0，在程序实现就是一个if-else语句，而sigmoid函数需要进行浮点四则运算，在实践中，使用ReLu激活函数神经网络通常会比使用sigmoid或者tanh激活函数学习的更快。

第二，sigmoid和tanh函数的导数在正负饱和区的梯度都会接近于 0，这会造成梯度弥散，而Relu和Leaky ReLu函数大于 0 部分都为常数，不会产生梯度弥散现象。(同时应该注意到的是，Relu进入负半区的时候，梯度为 0，神经元此时不会训练，产生所谓的稀疏性，而Leaky ReLu不会有这问题)

$z$ 在ReLu的梯度一半都是 0，但是，有足够的隐藏层使得 z 值大于 0，所以对大多数的训练数据来说学习过程仍然可以很快。

Softmax 函数

S o f t m a x (z_{i}) = \frac{e^{z_{i}}}{\sum_{c = 1}^{C} e^{z_{c}}}

Softmax 是用于多分类问题的激活函数，在多分类问题中，超过两个类标签则需要类成员关系。对于长度为 $K $ 任意实向量，Softmax 可以将其压缩为长度为 $K$ ，值在 $(0, 1)$ 围内，并且向量中元素的总和为 1 的实向量。

v2-11758fbc2fc5bbbc60106926625b3a4f_1440w

指数函数曲线呈现递增趋势，斜率逐渐增大，即 $x$ 上一个很小的变化，可以导致 $y$ 上很大的变化。但是当 $z_{i}$ 非常大时，可能导致结果溢出。

针对数值溢出有其对应的优化方法，将每一个输出值减去输出值中最大的值 $D = m a x (z)$ > $S o f t m a x (z_{i}) = \frac{e^{z_{i} - D}}{\sum_{c = 1}^{C} e^{z_{c} - D}}$

Softmax 与正常的 max 函数不同：max 函数仅输出最大值，但 Softmax 确保较小的值具有较小的概率，并且不会直接丢弃。我们可以认为它是 argmax 函数的概率版本或「soft」版本。

Softmax 激活函数的主要缺点是：

在零点不可微；
负输入的梯度为零，这意味着对于该区域的激活，权重不会在反向传播期间更新，因此会产生永不激活的死亡神经元。

Reference

https://zhuanlan.zhihu.com/p/105722023
通向概率分布之路：盘点 Softmax 及其替代品 (opens new window)

Swish 函数

函数表达式：y = x * sigmoid (x)

Swish 的设计受到了 LSTM 和高速网络中 gating 的 sigmoid 函数使用的启发。我们使用相同的 gating 值来简化 gating 机制，这称为 self-gating。

self-gating 的优点在于它只需要简单的标量输入，而普通的 gating 则需要多个标量输入。这使得诸如 Swish 之类的 self-gated 激活函数能够轻松替换以单个标量为输入的激活函数（例如 ReLU），而无需更改隐藏容量或参数数量。

Swish 激活函数的主要优点如下：

「无界性」有助于防止慢速训练期间，梯度逐渐接近 0 并导致饱和；（同时，有界性也是有优势的，因为有界激活函数可以具有很强的正则化，并且较大的负输入问题也能解决）；
导数恒 > 0；
平滑度在优化和泛化中起了重要作用。

Maxout 函数

在 Maxout 层，激活函数是输入的最大值，因此只有 2 个 maxout 节点的多层感知机就可以拟合任意的凸函数。

单个 Maxout 节点可以解释为对一个实值函数进行分段线性近似 (PWL) ，其中函数图上任意两点之间的线段位于图（凸函数）的上方。

Maxout 也可以对 d 维向量（V）实现：

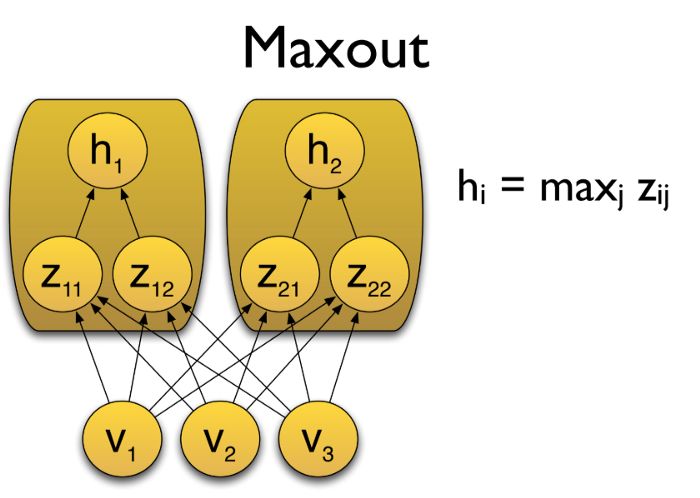
假设两个凸函数 h_1(x) 和 h_2(x)，由两个 Maxout 节点近似化，函数 g(x) 是连续的 PWL 函数。

因此，由两个 Maxout 节点组成的 Maxout 层可以很好地近似任何连续函数。

10. Softplus

Softplus 函数：f（x）= ln（1 + exp x）

Softplus 的导数为

f ′(x)=exp(x) / ( 1+exp⁡ x )

= 1/ (1 +exp(−x ))

，也称为 logistic / sigmoid 函数。

Softplus 函数类似于 ReLU 函数，但是相对较平滑，像 ReLU 一样是单侧抑制。它的接受范围很广：(0, + inf)。

快速概括一下不同激活函数的过程和结论。

sigmoid激活函数：除了输出层是一个二分类问题基本不会用它。

tanh激活函数**：tanh**是非常优秀的，几乎适合所有场合。

ReLu激活函数：最常用的默认函数，，如果不确定用哪个激活函数，就使用ReLu或者Leaky ReLu。公式 3.23： $a = m a x (0.01 z, z)$ 为什么常数是 0.01？当然，可以为学习算法选择不同的参数。

在选择自己神经网络的激活函数时，有一定的直观感受，在深度学习中的经常遇到一个问题：在编写神经网络的时候，会有很多选择：隐藏层单元的个数、激活函数的选择、初始化权值……这些选择想得到一个对比较好的指导原则是挺困难的。

鉴于以上三个原因，以及在工业界的见闻，提供一种直观的感受，哪一种工业界用的多，哪一种用的少。但是，自己的神经网络的应用，以及其特殊性，是很难提前知道选择哪些效果更好。所以通常的建议是：如果不确定哪一个激活函数效果更好，可以把它们都试试，然后在验证集或者发展集上进行评价。然后看哪一种表现的更好，就去使用它。

为自己的神经网络的应用测试这些不同的选择，会在以后检验自己的神经网络或者评估算法的时候，看到不同的效果。如果仅仅遵守使用默认的ReLu激活函数，而不要用其他的激励函数，那就可能在近期或者往后，每次解决问题的时候都使用相同的办法。

激活函数的导数（Derivatives of activation functions）

在神经网络中使用反向传播的时候，你真的需要计算激活函数的斜率或者导数。针对以下四种激活，求其导数如下：

1）sigmoid activation function

图 3.8.1

其具体的求导如下：公式 3.25： $\frac{d}{d z} g (z) = \frac{1}{1 + e^{- z}} (1 - \frac{1}{1 + e^{- z}}) = g (z) (1 - g (z))$

注：

当 $z$ = 10 或 $z = - 10$ ; $\frac{d}{d z} g (z) \approx 0$

当$z $= 0 , $\frac{d}{d z} g (z) =g(z)(1-g(z))= 1 / 4$

在神经网络中 $a = g (z)$ ; $g {(z)}^{^{'}} = \frac{d}{d z} g (z) = a (1 - a)$

Tanh activation function

图 3.8.2

其具体的求导如下：公式 3.26： $g(z) = tanh(z) = \frac{e^{z} - e^{-z}}{e^{z} + e^{-z}} $

公式 3.27： $\frac{d}{d z} g (z) = 1 - (t a n h (z))^{2}$ 注：

当 $z$ = 10 或 $z = - 10$ $\frac{d}{d z} g (z) \approx 0$

当 $z$ = 0, $\frac{d}{d z} g (z) =1-(0)= 1$

在神经网络中;

3）Rectified Linear Unit (ReLU)

$g (z) = m a x (0, z)$

g (z)^{^{'}} = {\begin{cases} 0 & if z < 0 \\ 1 & if z > 0 \\ u n d e f i n e d & if z = 0 \end{cases}

注：通常在 $z$ = 0 的时候给定其导数 1,0；当然 $z$ =0 的情况很少

4）Leaky linear unit (Leaky ReLU)

与ReLU类似

g (z) = max (0.01 z, z) g (z)^{^{'}} = {\begin{cases} 0.01 & if z < 0 \\ 1 & if z > 0 \\ u n d e f i n e d & if z = 0 \end{cases}

注：通常在 $z = 0$ 时候给定其导数 1,0.01；当然 $z = 0$ 情况很少。

参考：

[深度学习领域最常用的 10 个激活函数，一文详解数学原理及优缺点 - 知乎 (zhihu.com)](

上次更新: 2025/06/25, 11:25:50

← 调试策略 Embedding→