0. 摘要

本文聚焦于一个具有挑战性的问题——在线任务无关的类增量学习（OTFCIL）。与现有方法从数据流中持续学习特征空间不同，我们提出了一种新的计算 - 对齐范式。该范式首先为现有类计算一个最优几何结构（即类原型分布），并在新类出现时更新它，然后通过将深度神经网络模型的特征空间与最优几何结构对齐来进行训练。为此，我们开发了一种新的动态神经坍缩（DNC）算法来计算和更新最优几何结构。DNC 在新类出现时扩展几何结构而不损失其最优性，并确保旧类原型的漂移距离具有明确的上界。在此基础上，我们提出了一种新的动态特征空间自组织（DYSON）方法，包含三个主要组件：1）特征提取器，2）动态特征 - 几何对齐（DFGA）模块，将特征空间与 DNC 计算的最优几何结构对齐，以及 3）基于 DNC 几何的无训练类增量分类器。在 CIFAR10、CIFAR100、CUB200 和 CoRe50 四个基准数据集上的实验对比结果证明了 DYSON 方法的高效性和优越性。源代码发布于 https://github.com/isCDX2/DYSON。

1. 引言

在线任务无关的类增量学习（OTFCIL）[19, 34] 以连续数据流为输入，旨在通过在线学习逐步学习新出现的类，而无需任务边界和标识符。与传统的类增量学习 [12, 27, 32, 45, 49] 将数据流划分为一系列子集（称为会话或任务）不同，OTFCIL 是一个更为实际但更具挑战性的问题，因为样本是一次性提供的，且新旧类知识是混合的。

现有的 OTFCIL 方法根据知识学习和维护策略，主要分为三类：数据回放 [19, 34]、网络扩展 [39, 41] 和知识蒸馏 [2, 33] 方法。数据回放方法 [7, 34, 37, 43, 51] 存储少量旧类的训练样本或生成样本（称为示例），并在学习新类数据时回放它们以减轻旧类的灾难性遗忘。网络扩展方法 [32, 34, 39, 41, 47] 初始化一个新分支 [32, 39, 47]、新提示 [34] 或新分类器 [41] 来学习新类知识，并在增量学习过程中保持其他部分冻结以维护旧类知识。知识蒸馏方法 [17, 27, 30, 33, 37, 46] 将先前获得的模型视为教师模型，并通过逻辑 [27, 37]、特征 [17, 33] 和关系蒸馏 [30, 46] 将旧知识转移到新模型中。

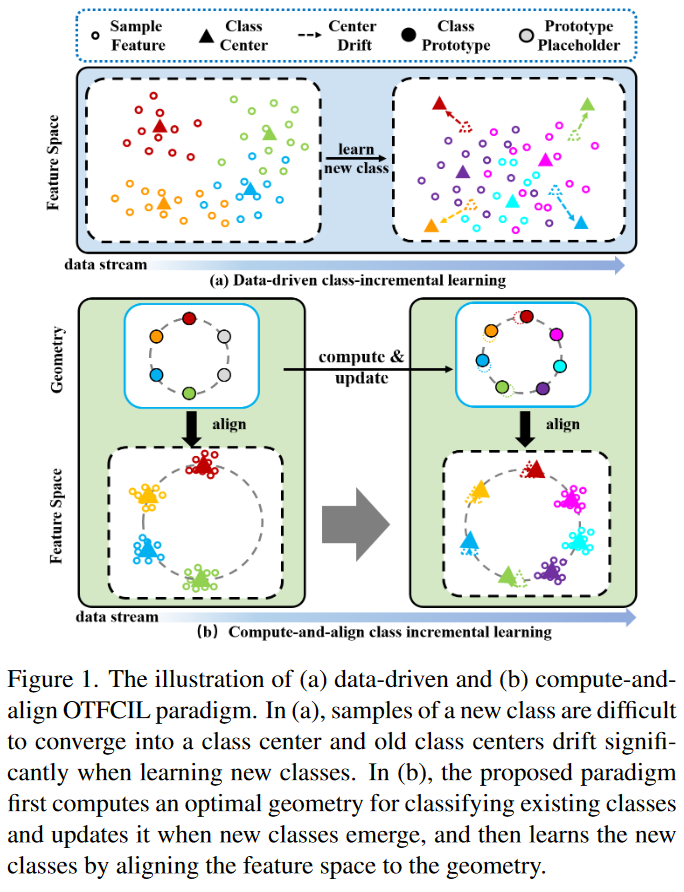
所有这些方法在增量学习过程中都不得不持续动态地调整其特征空间以适应无缝数据流。这种范式在学习新类时笨拙且在维护旧类时不稳定。如图 1（a）所示，在学习新类时，新类的特征难以收敛到某个类中心（即类内均值），因为中心会随着新样本的变化而变化，而旧类中心不可避免地会随着特征空间的调整而漂移。这在样本一次性提供（即在线学习）且新旧类数据混合（即没有任务边界和标识符）时尤为明显。

基于上述观察，我们思考，是否可以不从数据中学习特征空间几何，而是计算一个最优分类几何并在新类出现时动态更新它。在此基础上，OTFCIL 可以通过将特征空间与最优几何结构对齐来解决，即图 1（b）所示的计算 - 对齐范式。为此，我们提出了一种新的动态特征空间自组织（DYSON）框架，受到神经坍缩（NC）理论 [53] 的启发。NC 理论揭示了对于一个 K 类分类问题，在训练的最后阶段（训练误差为 0），同一类的最后一层特征将坍缩到一个 K 原型单形等角紧框架（ETF）。这些原型构建了一个最优分类几何结构，其中所有原型都是具有相同 l2 范数的单位向量，并且共享相同的对偶角，最大限度地分离特征空间。这为计算最优分类几何结构提供了机会。然而，由于原始的 NC 要求在训练期间预先定义并固定类的数量，因此它不适用于类增量学习。为了应对这一挑战，我们提出了一种新的动态神经坍缩（DNC）算法，能够随着不断出现的新类自适应地计算和更新最优几何结构。DNC 在新类出现时扩展几何结构而不损失其最优性，并确保旧类原型的漂移距离具有明确的上界。

在此基础上，我们提出了 DYSON 框架，包含三个主要组件：1）特征提取器，2）动态特征 - 几何对齐（DFGA）模块，将特征空间与 DNC 算法计算的最优几何结构对齐，以及 3）基于 DNC 几何的无训练类增量分类器。我们在 CIFAR10、CIFAR100、CUB200 和 CoRe50 四个基准数据集上进行了全面的实验，并与最先进的方法进行了比较。对比结果证明了 DYSON 的优越性和高效性。主要贡献总结如下：

• 我们提出了一种新的学习 - 对齐范式用于 OTFCIL，首先计算一个最优分类几何结构并在新类出现时更新它，然后将特征空间与该几何结构对齐。
• 我们设计了一种新的动态神经坍缩（DNC）算法，能够在不损失几何最优性的情况下扩展几何结构，并确保旧类原型的漂移具有明确的上界。
• 我们提出了一种新的动态特征空间自组织（DYSON）方法，包含特征提取器、动态特征 - 几何对齐（DFGA）模块和无训练类增量分类器。
• DYSON 在 CIFAR10、CIFAR100、CoRe50 和 CUB200 数据集上显著优于最先进的方法，分别提升了 8.9%、16.6%、26.8% 和 4.4%。

2. 相关工作

2.1. 类增量学习

现有的持续学习方法主要分为三类：数据回放、网络扩展和知识蒸馏方法。

数据回放方法通过存储或合成旧任务样本数据来防止模型发生灾难性遗忘。End-to-end [7]、iCaRL [37] 及其改进方法 [4, 11, 18] 基于 herding 算法选择存储的旧样本。此外，存储的旧任务数据也可以作为正则化约束。A-GEM [8] 使用新旧数据计算损失梯度向量的标量积，仅当标量积为正时更新参数。生成伪样本进行回放也可以有效缓解模型遗忘。ILUGAN [51] 通过生成对抗网络 [13] 生成伪样本以解决数据不平衡问题，类似的方法还有 [36] 和 [44]。

网络扩展方法通过冻结或隔离模型结构的一部分来减轻灾难性遗忘。[40] 冻结对特定任务最重要的权重，使其在反向传播时不更新。PackNet [32] 及其变体 [1] 为每个任务分配一部分参数空间，以隔离新旧任务参数。另一方面，一些基于架构的方法动态地向网络添加新层以增强模型学习新知识的能力，例如 [38, 48]。PNN [39]、Dytox [12]、Foster [47] 和 Der [52] 方法通过任务复制新组织来实现新旧知识的转移。

知识蒸馏被引入损失函数中，以使更新后的模型保留过去的记忆。权重蒸馏是一种基于正则化的方法。通过减少与先前任务相关的权重变化程度，权重保留了在旧任务中学到的知识。EWC [21] 提出使用 Fisher 信息矩阵计算权重的重要性，其变体方法 [2, 29, 56] 改进了重要性的计算。另一种正则化方法是数据正则化。LWF [27] 和 [10, 25] 等方法基于新任务数据的知识蒸馏，使新模型对新任务的预测与旧模型对新任务的预测相似。

除了上述三类方法外，CL 领域还有一些新的趋势。L2P [49] 使用预训练模型作为骨干网络，并通过学习提示来恢复知识。FearNet [20] 使用双重记忆系统来防止灾难性遗忘。混合系统模型也越来越常见。A-GEM [8] 结合了回放和正则化方法。DSDM [34] 在改变模型架构的同时使用动态记忆，因此它是基于架构和基于回放的混合方法。

2.2. 在线类增量学习

在线类增量学习旨在训练模型如何有效地从单次传输的在线数据流中学习知识。与离线学习相比，在线学习会限制模型的学习效率并加剧灾难性遗忘。该领域有许多算法从不同角度提出，例如 [3, 5, 14, 15, 28, 35, 42]。MIR [3] 提出根据梯度选择样本进行训练。DVC [14] 提出使用图像的互信息来充分探索单向数据流中的语义信息。GDUMB [35] 提出使用缓冲区数据重新训练模型以解决灾难性遗忘。[28] 将基于代理的损失与基于收缩的损失结合起来。

2.2.1 在线任务无关的类增量学习

与在线持续学习不同，在线任务无关的持续学习没有任务边界。为了解决 OTFCL 问题，一些方法随机初始化模型并从头开始训练。CoPE [9] 提出了一种架构，用于在 OTFCL 实验中平衡模型的稳定性和可塑性。考虑到梯度，GMED [19] 提出了一种策略，选择最能代表旧任务的样本数据。CN-DPM [26] 设计了一种可扩展的模型架构，突破了 OTFCL 的限制。然而，上述模型通过随机初始化进行训练，这使得它们的分类精度相对较低。因此，DSDM [34] 和 Ensemble [41] 提出使用预训练模型作为骨干网络来解决 OTFCL 问题，并取得了优异的成绩。DSDM [34] 根据特征的分布更新由位置向量和标签向量组成的单元池。Ensemble [41] 主要在单层线性中训练，以便在推理阶段与 NCM 分类器选择的类标签对应。

与我们的 DYSON 最相关的方法是 FCA [54]，它采用神经坍缩技术来解决少样本类增量学习问题。然而，DYSON 与 FAC 的差异和贡献是显著且重要的。首先，DYSON 具有技术能力（使用 DNC）为新出现的类增量更新几何结构，而 FCA 必须预先定义类的总数并在训练期间固定它。其次，FCA 依赖任务边界和标识符来区分新旧类知识，并使用存储旧类样本的缓冲区来缓解灾难性遗忘，而 DYSON 是一种在线任务无关的方法，不需要任何缓冲区。在第 5 节中，我们将 DYSON 与 FCA 进行比较，以展示所提出方法的效率和优越性。

3. 预备知识

神经坍缩（NC）[53] 揭示了一个现象，即在分类任务的训练末期（训练误差为 0），最后一层特征空间的最优几何结构可以由一个单形等角紧框架（ETF）定义。

3.1 单形等角紧框架的定义

对于一个 K 类分类问题，其 K 个类的类内均值对应于一个 K 原型的单形 ETF，其中原型 $m^i\in {\mathbb{R}}^d,i=1,...,K$ 可以通过以下公式获得：

$$\begin{array}{}\text{(1)}& M=\sqrt{\frac{K}{K-1}}U(I_K-\frac{1}{K}{\mathbf{1}}_{K_t}{\mathbf{1}}_K^T),\end{array}$$

其中 $M=[m_1,...,m_K]\in {\mathbb{R}}^{d\times K}$，$U\in {\mathbb{R}}^{d\times K}$ 是一个随机初始化的正交矩阵，满足 $U_{t}U=I_K$，$I_K$ 是一个 K 维单位矩阵，${\mathbf{1}}_K$ 是一个全 1 向量。

单形 ETF 中的原型构建了一个最优的分类几何结构，其中所有原型都是具有相同 $l_2$ 范数的单位向量，并且通过相同的对偶角最大化地分离特征空间，即：

$$\begin{array}{}\text{(2)}& m_t^i{m}^j=\frac{K}{K-1}{\delta }_{i,j}-\frac{1}{K-1},\mathrm{\forall }i,j\in [1,...,K],\end{array}$$

其中 ${\delta }_{i,j}=1$ 当 $i=j$，否则为 0。对偶角 $-\frac{1}{K-1}$ 是 d 维特征空间中 K 个向量的最大等角分离。

基于上述定义，NC 现象可以总结为：

(NC1) 类内最后一层特征坍缩：同一类的最后一层特征将坍缩到其类内均值，即 ${\mathrm{\Sigma }}_W\to 0$，其中 ${\mathrm{\Sigma }}_W={\text{Avg}}_{i,k}\{(h_{i,k}-h_k)(h_{i,k}-h_k{)}_t\}$。$h_{i,k}$ 是第 k 类第 i 个样本的最后一层特征，$h_k={\text{Avg}}^i(h_{i,k})$ 是第 k 类的类内均值。

(NC2) 收敛到单形 ETF：类内均值以全局均值 $h_G={\text{Avg}}_{i,k}(h_{i,k})$ 为中心，即 ${\tilde{h}}_k=(h_k-h_G)/||h_k-h_G||$ 将收敛到公式 (1) 中定义的单形 ETF 的原型。

(NC3) 自对偶性：第 k 类的分类器权重 $w_k$ 与其全局中心类内均值 ${\tilde{h}}_k=w_k/||w_k||$ 平行（对齐）。

(NC4) 简化为最近类中心预测：$\arg \underset{k}{max}⟨h,w_k⟩=\arg \underset{k}{min}||h-w_k||$，其中 $h$ 是输入样本的最后一层特征。

4. 方法论

4.1. 问题公式化

设 $D=\{B_1,B_2,...,B_T\}$ 为一个长度为 $T$（对于无限数据流 $T\to \mathrm{\infty }$）的输入数据流，其中每个元素 $B_t=\{(X_t^i,y_t^i){\}}_{i=1}^N$ 表示第 $t$ 个样本批次，$N$ 为批次大小。$X_t^i\in {\mathbb{R}}^{W\times H}$ 表示 $B_t$ 中的第 $i$ 张图像，$y_t^i\in {\mathcal{C}}_t$ 表示其对应的类标签，其中 ${\mathcal{C}}_t$ 是 $B_t$ 的类集合。根据 OTFCL 设置 [34]，每个样本是一次性提供的，即 $\mathrm{\forall }i\ne j,B^i\cap B^j=\mathrm{\varnothing }$，并且不同批次之间没有任务边界。OTFCL 的目标是通过在线训练（即训练轮次为 1）训练一个统一的模型，能够逐步学习和识别 $D$ 中不断出现的新类。在每个训练步骤 $t$，我们只能访问当前数据批次 $B_t$，而之前的批次 $B_1,...,B_{t-1}$ 不可用。在评估时，模型应能够识别所有遇到的类 ${\mathcal{C}}_{1\sim t}={\mathcal{C}}_1\cup \cdots \cup {\mathcal{C}}_t$。

4.2. 框架概述

图 2 展示了我们提出的 DYSON 方法的框架，它是一个在线且参数高效的学习模型，包含三个主要组件：(a) 一个预训练的特征提取器骨干 $f(\cdot ;\mathrm{\Theta })$，(b) 一个动态特征 - 几何对齐（DFGA）模块，包含一个特征投影层 $g(\cdot ;\mathrm{\Phi })$，以及 (c) 一个无训练的类增量分类器 $h(\cdot ;Z)$，其中 $\mathrm{\Theta }$、$\mathrm{\Phi }$ 和 $Z$ 分别是三个组件的参数集。在增量学习过程中，特征提取器 $f(\cdot ;\mathrm{\Theta })$ 和分类器 $h(\cdot ;Z)$ 的参数被冻结且无需训练，只有投影层 $g(\cdot ;\mathrm{\Phi })$ 被优化以将特征空间与 DNC 算法计算的最优几何结构对齐。

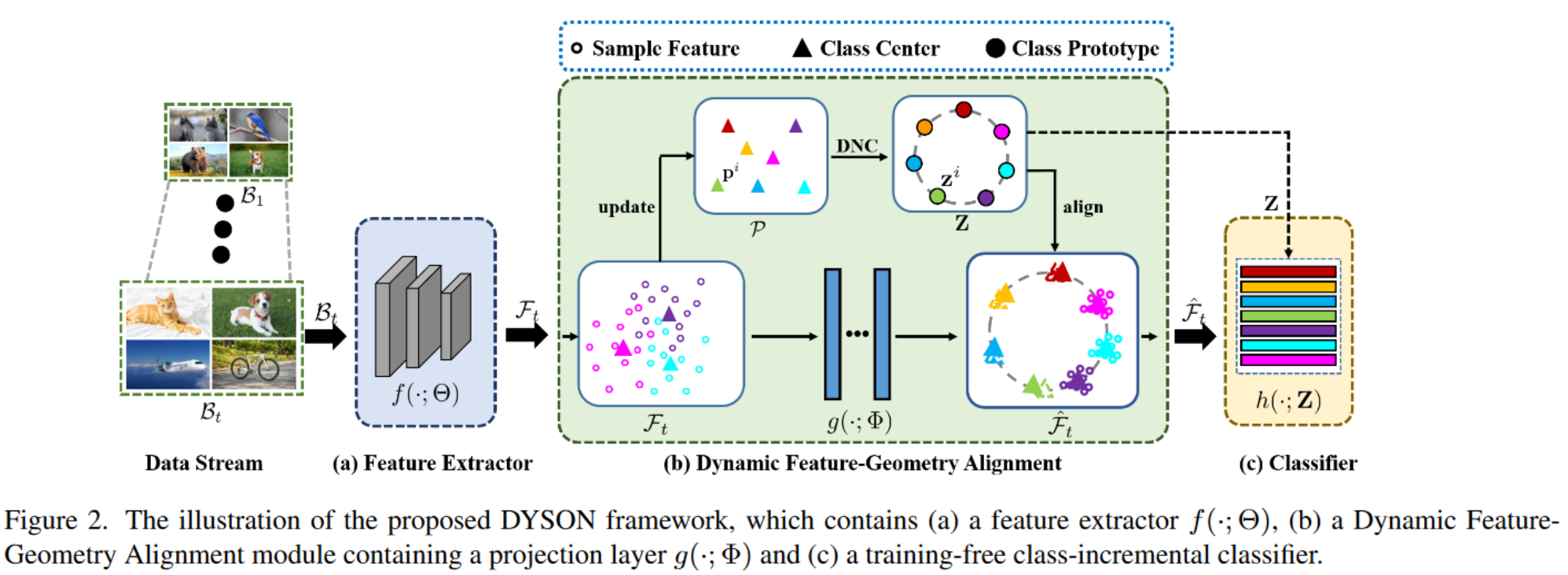
具体来说，开始时我们初始化一个空集 $\mathcal{P}=\{\}$ 来存储类中心。

特征提取器：在每个步骤 $t$，以样本批次 $B_t$ 为输入，模块 (a) 输出 $B_t$ 的特征集合 $F_t$：

$$\begin{array}{}\text{(3)}& f_t^i=f(X_t^i;\mathrm{\Theta }),\end{array}$$$$\begin{array}{}\text{(4)}& F_t=\{f_t^i|i=1,...,|B_t|\},\end{array}$$

其中 $f_t^i\in {\mathbb{R}}^{d\times 1}$ 是 $X_t^i$ 的特征，$d$ 是特征维度。

动态特征 - 几何对齐：以特征集 $F_t$ 为输入，我们首先为每个类 $j\in {\mathcal{C}}_t$ 计算类内均值 $p_t^j\in {\mathbb{R}}^d$，其中 $p_t^j=\text{avg}(\{f_t^i|\mathrm{\forall }i,y_t^i=j\})$ 计算 $F_t$ 中第 $j$ 类特征的平均值。对于每个类 $j\in {\mathcal{C}}_t$，如果 $j$ 是新类（即 $j\notin {\mathcal{C}}_{1\sim t-1}$），我们将 $p_t^j$ 初始化为类 $j$ 的中心 $p^j$；如果 $j$ 是旧类（即 $j\in {\mathcal{C}}_{1\sim t-1}$），我们通过移动平均更新类 $j$ 的中心 $p^j$：

$$\begin{array}{}\text{(5)}& \mathrm{\forall }j\in {\mathcal{C}}_t,p^j=\{\begin{array}{ll}{p}_t^j,& \text{if }j\notin {\mathcal{C}}_{1\sim t-1},\\ \beta \cdot p^j+(1-\beta )\cdot p_t^j,& \text{if }j\in {\mathcal{C}}_{1\sim t-1},\end{array}\end{array}$$

其中 $\beta$ 是更新率。输出集 $\mathcal{P}$ 收集所有遇到的类的中心，即 $\mathcal{P}=\{p_1,...,p_{K_t}\}$，其中 $K_t=|{\mathcal{C}}_{1\sim t}|$ 表示当前遇到的类的总数。

在此基础上，我们使用动态神经坍缩（DNC）算法计算当前 $K_t$ 个类的类原型 $Z$：

$$\begin{array}{}\text{(6)}& Z=[z_1,...,z_{K_t}]={\varphi }_{\text{dnc}}(\mathcal{P}),\end{array}$$

其中 $Z\in {\mathbb{R}}^{d\times K_t}$ 输出 $K_t$ 个类的类原型的拼接矩阵，每个列向量 $z^j\in {\mathbb{R}}^{d\times 1}$ 对应第 $j$ 个类的原型。值得注意的是，类原型 $Z$ 仅在出现新类时通过公式 (6) 更新。在第 4.4 节中，我们证明了 $Z$ 中的原型构建了一个满足公式 (2) 的最优分类几何结构，并且旧类原型的漂移距离在几何更新后具有明确的上界。

在训练过程中，在每个学习步骤 $t$，我们通过高斯噪声 [57] 对旧类的中心 $p^j$ 进行增强，生成一组伪特征 $V_t=\{v_1^t,...,v_N^t\}$，其中 $v_t^i$ 表示第 $i$ 个伪特征，$|V_t|=|B_t|=N$。通过使用投影层 $g(\cdot ;\mathrm{\Phi })$ 将样本特征 $f_t^i$ 和伪特征 $v_t^i$ 投影到其对应的类原型上，我们将特征空间与 $Z$ 构建的最优几何结构对齐。特征 - 几何对齐的目标可以表示为：

$$\begin{array}{}\text{(7)}& {\mathcal{L}}_{\text{AL}}=\frac{1}{|B_t|}\sum _{i=1}^{|B_t|}||g(f_t^i;\mathrm{\Phi })-\sigma (Z,f_t^i)|{|}^2+\frac{1}{|V_t|}\sum _{i=1}^{|V_t|}||g(v_t^i;\mathrm{\Phi })-\sigma (Z,v_t^i)|{|}^2,\end{array}$$

其中 $\sigma (Z,f_t^i)$ 和 $\sigma (Z,v_t^i)$ 根据输入特征 $f_t^i$ 和 $v_t^i$ 的类标签输出对应的类原型 $z^j\in Z$。我们使用 ${\hat{f}}_t^i=g(f_t^i;\mathrm{\Phi })$ 表示 $f_t^i$ 的投影特征。模块 (b) 输出投影特征的集合 ${\hat{F}}_t=\{{\hat{f}}_t^1,...,{\hat{f}}_t^N\}$。

无训练的类增量分类器：由于同一类的投影特征 $v_t^i$ 坍缩到类原型 $z^j$，并且类原型是具有相同对偶角的单位向量，我们将每个原型 $z^j$ 视为第 $j$ 类的分类权重，并构建一个权重为 $Z=[z_1,...,z_{K_t}]$ 的线性分类器。给定样本 $X_t^i$ 的投影特征 ${\hat{f}}_t^i$，分类可以通过以下公式解决：

$$\begin{array}{}\text{(8)}& h({\hat{f}}_t^i;Z)=\arg \underset{z^j}{max}{\hat{f}}_t^{i^T}[z_1,...,z_{K_t}].\end{array}$$

当新类出现时，我们通过更新由 DNC 计算的 $Z$ 来扩展分类器。

损失函数：在训练过程中，以每个样本批次 $B_t$ 为输入，我们使用公式 (7) 中的特征 - 几何对齐损失 ${\mathcal{L}}_{\text{AL}}$ 和交叉熵损失 [24] 来优化投影层 $h(\cdot ;\mathrm{\Phi })$：

$$\begin{array}{}\text{(9)}& \underset{\mathrm{\Phi }}{min}{\mathcal{L}}_{\text{total}}(B_t;\mathrm{\Theta },\mathrm{\Phi },Z)={\mathcal{L}}_{\text{AL}}+{\mathcal{L}}_{\text{CE}}.\end{array}$$

4.3. 动态神经坍缩

在以下描述中，我们省略了下标 $t$ 以简化描述。以类中心集 $\mathcal{P}$ 为输入，我们将类中心拼接成矩阵 $P=[p_1,...,p_K]\in {\mathbb{R}}^{d\times K}$，其中 $p^j\in {\mathbb{R}}^{d\times 1}$ 是第 $j$ 个类中心，$K$ 是类的数量。我们首先计算矩阵 $P$ 的 QR 分解：

$$\begin{array}{}\text{(10)}& P=QR,\end{array}$$

其中 $Q=[q_1,...,q_K]\in {\mathbb{R}}^{d\times K}$ 是一个正交矩阵，满足 $Q_{t}Q=I_K$，$R\in {\mathbb{R}}^{K\times K}$ 是一个上三角矩阵。然后我们使用 $Q$ 计算类原型矩阵 $Z$：

$$\begin{array}{}\text{(11)}& Z=\sqrt{\frac{K}{K-1}}Q(I_K-\frac{1}{K}{\mathbf{1}}_{K_t}{\mathbf{1}}_K^T),\end{array}$$

其中 $Z=[z_1,...,z_K]\in {\mathbb{R}}^{d\times K}$ 是 $K$ 个类原型的拼接矩阵，$z^j\in {\mathbb{R}}^{d\times 1}$ 是第 $j$ 个类的原型。$I_K$ 是一个 $K$ 维单位矩阵，${\mathbf{1}}_K$ 是一个全 1 向量。$Z$ 中的原型构建了一个 $K$ 类分类的最优几何结构，对于任意 $z^i$ 和 $z^j$，我们有：

$$\begin{array}{}\text{(12)}& \mathrm{\forall }i,j,z_t^i{z}^j=\frac{K}{K-1}\cdot q_t^i{q}^j-\frac{1}{K-1},\end{array}$$

其中所有原型都是单位向量，即 $\mathrm{\forall }i,||z^i|{|}^2=z_t^i{z}^i=1$，并且任意两个原型之间的角度相同，即 $\mathrm{\forall }i\ne j,z_t^i{z}^j=-\frac{1}{K-1}$。

原型更新：当出现 $C$ 个新类时，我们有 $\mathcal{P}=\{p_1,...,p_K;p_{K+1},...,p_{K+C}\}$。我们将 $\mathcal{P}$ 拼接成 $P^{\prime }=[p_1,...,p_{K+C}]$，并使用公式 (10) 和 (11) 计算更新后的类原型 $Z^{\prime }=[z_1^{\prime },...,z_K^{\prime };z_{K+1}^{\prime },...,z_{K+C}^{\prime }]$。旧类原型的漂移距离可以通过以下公式计算：

$$\begin{array}{}\text{(13)}& ||z^i-z^{i^{{}^{\prime }}}|{|}^2=2-2\sqrt{\frac{(K-1)(K+C)}{K(K+C-1)}}.\end{array}$$

在第 4.4 节中，我们证明了 DNC 在不损失几何最优性的情况下将几何结构从 $K$ 个原型扩展到 $K+C$ 个原型，并且旧类原型的漂移距离 $||z^i-z^{i^{{}^{\prime }}}|{|}^2,\mathrm{\forall }i\le K$ 具有明确的上界。

提高几何稳定性：在类数量 $K$ 较少的早期学习阶段，$Z$ 中的类原型分布较为稀疏，旧类原型的漂移距离较大。这导致几何结构在维护旧知识时不够稳定。为了提高增量学习过程中几何结构的稳定性，我们向 DNC 引入了原型占位符 $E\in {\mathbb{R}}^{d\times M}$，其中 $M$ 是占位符的数量。

具体来说，我们初始化一个随机正交矩阵 $E=[e_1,...,e_M]\in {\mathbb{R}}^{d\times M}$，其中 $M$ 个占位符满足 $\mathrm{\forall }i\ne j,e_t^i{e}^j=0$。以类中心矩阵 $P\in {\mathbb{R}}^{d\times K}$ 为输入，当 $K<M$ 时，我们首先使用占位符对 $P$ 进行填充：

$$\begin{array}{}\text{(14)}& P_{\text{pad}}=[p_1,...,p_K;e_{K+1},...,e_M],\end{array}$$

然后使用公式 (10) 和 (11) 计算类原型 $Z=[z_1,...,z_K;z_{K+1},...,z_M]$，并选择前 $K$ 列作为 $K$ 个类的原型。当 $K\ge M$ 时，我们直接使用 $P$ 计算 $Z$。在此基础上，旧类原型的漂移距离具有明确的上界：

$$\begin{array}{}\text{(15)}& ||z^i-z^{i^{{}^{\prime }}}|{|}^2\le 2-2\sqrt{\frac{(M-1)(M+C)}{M(M+C-1)}},\end{array}$$

其中 $C$ 是新出现的类的数量。通过公式 (15)，DNC 几何结构的稳定性得到了保证。

4.4. 理论分析

定理 1：在增量学习过程中，DNC 算法将具有 $K$ 个原型的单形 ETF 扩展到具有 $K+C$ 个原型的单形 ETF，且不损失几何最优性，即 $Z^{\prime }$ 中的原型满足：

$$\begin{array}{}\text{(16)}& \mathrm{\forall }i,j,z^{{i^{{}^{\prime }}}^T}{z}^{j^{{}^{\prime }}}=\frac{K+C}{K+C-1}{\delta }_{i,j}-\frac{1}{K+C-1},\end{array}$$

其中 ${\delta }_{i,j}=1$ 当 $i=j$，否则为 0。$Z^{\prime }$ 中的原型构建了一个 $K+C$ 类分类的最优几何结构，其中所有向量都是单位向量（即 $\mathrm{\forall }i,||z^{i^{{}^{\prime }}}|{|}^2=z_t^{i^{{}^{\prime }}}{z}^{i^{{}^{\prime }}}=1$），并且具有相同的对偶角，最大限度地分离了特征空间（即 $\mathrm{\forall }i\ne j,z^{{i^{{}^{\prime }}}^T}{z}^{j^{{}^{\prime }}}=-\frac{1}{K+C-1}$）。该定理允许我们在新类出现时使用 DNC 算法自适应地更新最优分类几何结构，并通过将特征空间与最优几何结构对齐来增量训练统一模型。定理 1 的证明见附录 A。

定理 2：当出现 $C$ 个新类时，使用 DNC 算法将现有的 $K$ 类原型扩展到 $K+C$ 个原型，并引入 $M$ 个原型占位符，旧类原型的漂移距离具有明确的上界，即 $\mathrm{\forall }i=1,...,K$，$||z^i-z^{i^{{}^{\prime }}}|{|}^2\le 2-2\sqrt{\frac{(M-1)(M+C)}{M(M+C-1)}}$，其中 $z^i$ 和 $z^{i^{{}^{\prime }}}$ 分别是类 $i$ 的旧和新原型。该定理保证了在学习新类时旧类几何结构的稳定性。定理 2 的证明见附录 B。

5. 实验

在本节中，我们在四个基准数据集上进行了全面的实验，以展示所提出方法的优越性和通用性。

5.1. 数据集和评估细节

我们在四个基准数据集上进行了实验，包括 CIFAR-10 [23]、CIFAR-100 [23]、CUB-200 [50] 和 CoRe50 [31]，以验证所提出的 DYSON 方法的效率和有效性。

数据集：CIFAR-10 [23] 包含 10 个类别的 60,000 张图像，其中 50,000 张用于训练，其余用于测试。图像分辨率为 32×32。CIFAR-100 [23] 包含 100 个类别的 60,000 张图像，每个类别包含 600 张图像，其中 500 张用于训练，100 张用于测试。CUB-200 [50] 包含 200 个鸟类类别的 11,788 张图像，每个类别大约有 30 张训练图像和 29 张测试图像。CoRe50 [31] 包含 50 个类别，总共 164,866 张图像，每个类别大约有 2,400 张训练图像和 900 张测试图像。

评估协议：为了公平比较，我们遵循 [34, 41] 中的评估协议，在四个基准数据集上进行了 n 步比较结果。n 步协议表示，按照随机的类顺序，每个增量学习阶段包含 n 个类。例如，对于 10 个类的 2 步增量学习，OTFCIL 包含 5 个增量学习阶段，每个阶段包含 2 个类。我们进行了 1 步、2 步、5 步和高斯步的评估。

评估指标：我们采用广泛使用的平均准确率（Avg）和最后一步准确率（Last）来评估所提出的方法。Avg 是每个学习阶段后准确率的平均值，Last 是所有类别上的最终准确率。我们在配备 NVIDIA 3090TiGPU 的 PC 上进行实验，每个实验运行 5 次并报告平均性能。

实现细节：与最先进的 OTFCIL 方法 [34]、CoPE [9] 和 Ensemble [41] 类似，我们使用在 ImageNet 上预训练的 ResNet50 [16] 和 ViT-S/8 [6] 作为特征提取器骨干，并移除分类器。我们设置批量大小 $N=50$，原型占位符的数量 $M=10$。我们使用 Adam 优化器进行训练，学习率 $lr=2e-5$，权重衰减 $weight\mathrm{\_}decay=5e-6$。在公式 (5) 中设置中心更新率 $\beta =0.3$。

5.2. 与最先进方法的比较

在线任务无关的类增量学习：在表 1 中，我们将 DYSON 方法与最先进的 OTFCIL 方法进行比较，包括 CoPE [9]、CN-DPM [26]、GMED [19]、FCA [54]、Ensemble [41] 和 DSDM [34]，以及代表类增量学习的 L2P [49] 方法。与最近的工作 DSDM 类似，我们在 CIFAR-10 和 CIFAR-100 数据集上报告了 1 步、2 步、5 步和高斯步评估协议下的最后准确率（Last），其中比较的方法使用与我们相同的 ResNet50 和 ViT-S/8 作为骨干网络。从表中可以看出：1）通过计算 DNC 几何结构并使用新类特征和旧类伪特征将特征空间与几何结构对齐，DYSON 是一种无需存储任何旧类样本的无缓冲区方法，能够有效缓解灾难性遗忘。2）与使用 1k 旧类样本存储的竞争性 DSDM 方法相比，DYSON 在 CIFAR-10 和 CIFAR-100 数据集上显著且稳定地优于 DSDM。在 CIFAR-10 数据集上，使用相同的 ViT-S/8 骨干网络，DYSON 在 1 步、2 步和高斯步协议下分别比 DSDM 高出 7.1%、7.9% 和 8.9%。在更具挑战性的 CIFAR-100 数据集上，使用相同的 ViT-S/8 骨干网络，DYSON 在 1 步、2 步和高斯步协议下分别比 DSDM 高出 16.1%、14.8% 和 15.0%。这些结果证明了 DYSON 方法的优越性。3）使用 ResNet50 和 ViT-S/8 作为骨干网络，DYSON 在所有情况下都显著优于最先进的方法，展示了其对不同骨干网络的鲁棒性。

在线类增量学习：遵循 [15, 34] 中的在线 CIL 设置，我们在表 2 中对 CIFAR-10 和 CoRe50 数据集进行了实验比较。CIFAR-10 在 2 步评估协议下进行评估，其中学习过程分为 5 个学习阶段，每个阶段包含两个新类的样本。CoRe50 分为 9 个学习阶段，第一个阶段学习 10 个类，后续增量阶段学习 5 个类。我们将提出的方法与最先进的在线 CIL 方法进行比较，包括 A-GEM [8]、MIR [3]、GSS [5]、ASER [42]、GDUMB [35] 和 Candidates Voting [15]。为了公平比较，所有比较方法（包括 DYSON）使用相同的 ImageNet 预训练 ResNet18 作为骨干网络。从表 2 中可以看出：1）所有现有的最先进方法都严重依赖于存储旧类样本（即缓冲区大小）来解决具有挑战性的在线增量学习问题，存储的样本越多，它们的准确率越高。2）提出的 DYSON 方法无需存储旧类样本，并显著优于基于缓冲区的方法。特别是在 CoRe50 数据集上，DYSON 在平均准确率（Avg）和最后准确率（Last）上分别比竞争性 DSDM-1k 高出 26.8% 和 18.0%，并比 DSDM-5k 高出 4.4% 和 4.2%。

离线任务无关的类增量学习：此外，在表 3 中，我们还在 CIFAR-100 和 CUB-200 数据集上进行了离线 TFCIL 性能评估。遵循 [20, 51] 中的设置，所有比较方法使用 ImageNet 预训练的 ResNet50 作为骨干网络，现有方法使用 3k 缓冲区大小存储旧类样本。从表中可以看出，DYSON 在所有情况下都显著优于现有方法。与竞争性 DSDM 方法相比，DYSON 在 CIFAR-100 数据集的 2 步和 5 步协议下分别实现了 8.4% 和 8.7% 的平均准确率提升，在 CUB-200 数据集上分别实现了 3.2% 和 4.4% 的提升。

性能分析：我们可以看到，DYSON 在无需使用任何缓冲区的情况下显著优于现有的最先进方法。性能的提升来自两个方面：首先，学习 - 对齐范式，首先为出现的类计算最优几何结构，然后将特征空间与该几何结构对齐。其次，提出的 DNC 算法在新类出现时计算和更新几何结构，它在不损失结构最优性的情况下扩展几何结构，并确保旧类原型的漂移具有明确的上界，从而保证了旧知识的稳定性。

5.3. 消融实验

超参数 $M$ 的影响：在表 4 中，我们在 CIFAR-100 数据集上进行了 5 步评估协议下的消融实验，分析了参数 $M$ 对最后准确率的影响。$M$ 是占位符的数量，影响 DNC 几何结构的稳定性。从表中可以看出，当 $M=0$ 时，性能在平均准确率和最后准确率上都较差。这是因为在早期 CIL 阶段，没有占位符的几何结构不稳定。当 $10\le M\le 100$ 时，随着 $M$ 的增加，性能保持稳定。当 $M=200$ 时，性能略有下降，因为过多的占位符阻碍了新类的学习。根据实验结果，我们在所有实验中固定 $M=10$。

不使用标签注释的预训练骨干网络：为了消除四个基准数据集中的新类是否已经被 ImageNet 预训练模型学习过的担忧，在表 5 中，我们使用自监督的 DINO-ResNet50 骨干网络 [6] 进行了消融实验。DINO-ResNet50 通过自监督信息蒸馏进行预训练，在训练过程中未使用类别信息。从表中可以看出，使用 DINO-ResNet50 进一步提高了性能，这证明了所提出方法在学习新类方面的能力。

6. 结论

我们提出了一种新的 DYSON 方法，包含特征提取器骨干、动态特征 - 几何对齐（DFGA）模块和无训练类增量分类器，用于解决具有挑战性的 OTFCIL 问题。它遵循一种新的学习 - 对齐范式，首先为现有类计算最优分类几何结构并在新类出现时更新它，然后将特征空间与该几何结构对齐。我们推导了动态神经坍缩（DNC）算法来计算和更新几何结构，其中几何结构在不损失最优性的情况下进行更新，并且旧类原型的漂移具有明确的上界。