Graph Convolutional Network

Overview

1. 在CNN、RNN如此强大的模型之后，为什么出现GCN？

   CNN：针对图像（二维数据结构，矩阵形式。Eucliden Structure），它的核心在于其kernel，一个滑动窗口，通过卷积来提取特征。因为图像具有平移不变性：滑动窗口无论移动到图片的哪一个位置，其内部的结构都是一模一样的，因此CNN可以实现参数共享。这就是CNN的精髓所在。

   RNN：针对自然语言（序列信息，一维结构），通过各种门的操作，使得序列前后的信息互相影响，从而很好地捕捉序列的特征。

   GCN：针对图结构，即Non Eucliden Structure，拓扑结构。如社交网络、化学分子结构、知识图谱等等。

   GCN实际上可以看作一个特征提取器（类似于CNN的作用），不同的是它的处理对象为图结构数据。利用GCN提取出的特征，我们可以实现节点分类（node classification）、图分类（graph classification）、边预测（link prediction），还可以得到图的嵌入表示（graph embedding）。

2. 卷积

   离散卷积本质上是一种加权求和。CNN中的卷积本质上就是利用一个共享参数的过滤器（Kernel)，通过计算中心像素点及相邻像素点的加权和来构成feature map实现空间的特征提取，加权系数就是卷积核的权重系数（先初始化，然后根据误差函数通过反向传播梯度下降进行迭代优化）

3. 拓扑图空间特征提取两种方式

   • vertex domain：提取拓扑图上的空间特征，然后把每个顶点相邻的neighbors找出来
   • spectral domain：借助图谱的理论实现拓扑图上的卷积操作（借助于图的拉普拉斯矩阵的特征值和特征向量）

4. 图的拉普拉斯矩阵

   对于图$G=(V,E)$，其Laplacian 矩阵的定义为 $L=D-A$，

   $L$ 为拉普拉斯矩阵Laplacian matrix; $D$ 为对角度矩阵Degree matrix，对角线上的元素是顶点的度，即该元素链接的元素的个数; $A$ 邻接矩阵 Adjacency matrix ,即表示任意两个顶点之间的邻接关系，邻接则为1，不邻接则为0。

   

   物理意义：这个矩阵描述图的拉普拉斯矩阵与图的性质之间的关系。拉普拉斯矩阵与图的性质满足 $L=D-A$ 种矩阵关系，其中图$G=(V,E)$ 性质，体现在图的邻接矩阵$A$ 图的度矩阵$D$ 。

   在理解了这个的基础上，还有其他的几种拉普拉斯矩阵，上面这种拉普拉斯矩阵只是其中的一种，下面几种拉普拉斯矩阵在不同的任务中有不同的运用。

   Combinatorial Laplacian $L=D-A$ Symmetric normalized Laplacian $L^{sys}={\tilde{D}}^{-\frac{1}{2}}L{\tilde{D}}^{-\frac{1}{2}}$ Random walk normalized Laplacian $L^{rw}=D^{-1}L$ 通过上面的公式的物理意义，我们知道了，图的性质可以表示在拉普拉斯矩阵之中，即图的性质可以通过拉普拉斯矩阵体现出来。这样，我们将图的分析，可以变为对拉普拉斯矩阵的分析。

   5.why Laplacian

   • 拉普拉斯矩阵是对称矩阵，可以进行特征分解；
   • 拉普拉斯矩阵只在中心顶点和一阶相连的顶点上（1-hop neighbor）有非0元素，其余均为0；

**二、**Theory

它是一个神经网络层，且仅仅是一个全连接层。（下图是一个2层的GCN例子）

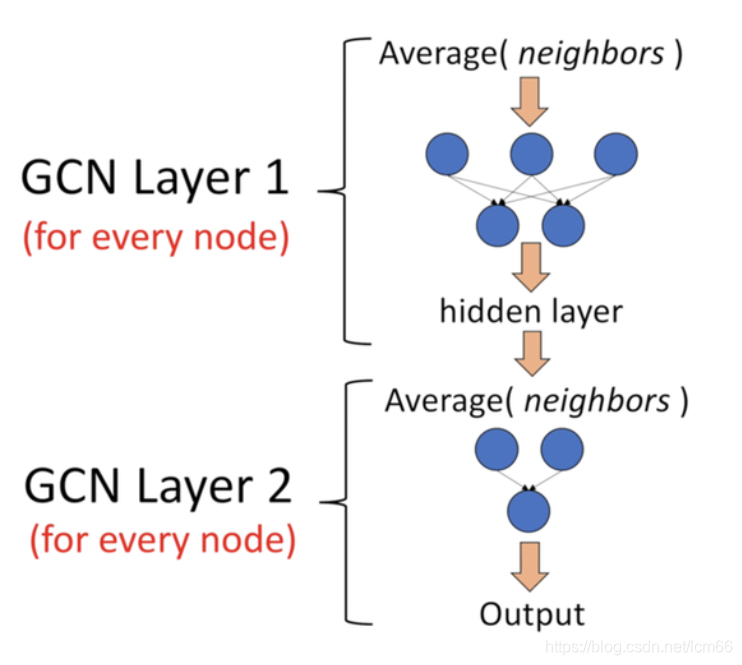
假设有一组图数据，包含$N$ 节点（node），每个节点有自己的特征信息，我们设这些节点的特征组成一个$N\times D$ 的矩阵$X$，然后各个节点之间的关系也会形成一个$N\times N$ 的矩阵$A$，即邻接矩阵（adjacency matrix）。那么$X$ $A$ 是我们模型的输入。

该网络的传播方式为：

$$H^{(l+1)}=\sigma ({\tilde{D}}^{-\frac{1}{2}}\tilde{A}{\tilde{D}}^{-\frac{1}{2}}{H}^{(l)}{W}^{(l)})$$

其中，

（1）$\tilde{A}$=$A+I$，$I$ 单位矩阵；

（2）$\tilde{D}$ $\tilde{A}$ 度矩阵（degree matrix）；

（3）$H$ 每一层的特征，对于输入层的话，$H_0$ 是$X$；

（4）$\sigma$ 非线性激活函数。

至于为什么要这样去设计一个公式，先不考虑。现在只需要知道${\tilde{D}}^{-\frac{1}{2}}\tilde{A}{\tilde{D}}^{-\frac{1}{2}}$ 个部分是可以事先计算得到的，因为$\tilde{D}$ $A$ 算得来，而$A$ 输入之一。对于不需要去了解数学原理、只想应用GCN来解决实际问题的人来说，就只需知道：这个GCN设计了一个强大的公式，用这个公式就可以很好地提取图的特征。

进一步理解。引用一张图：

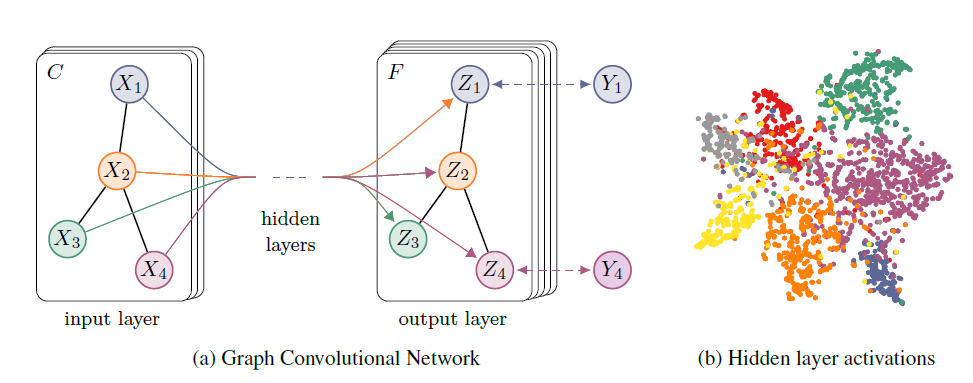
上图中的GCN输入一个图，通过若干层GCN每个node的特征从$X$ 成了$Z$，但是，无论中间有多少层，**node之间的连接关系，即$A$，都是共享的。**也就是说解决了上面说的不具备平移不变性问题。其思路是：借鉴CNN，将卷积分为三步：

（1）选定中心节点后，确定邻域：对每个节点选择固定个数的节点作为邻居；

（2）给邻域结点编号；

（3）参数共享：选择固定大小的窗口进行参数共享。

参考论文作者，由简入繁：

每一层GCN的输入都是邻接矩阵$A$ node的特征$H$，那么我们考虑直接做一个内积，再乘一个参数矩阵W，然后激活一下，就相当于一个简单基础的神经网络层嘛。如下：

$$f(H^{(l)},A)=\sigma (A{H}^{(l)}{W}^{(l)})$$

实验证明，即使就这么简单的神经网络层，就已经很强大。

上面这个简单的模型存在几个局限：

（1）由于$A$ 对角线上都是0，所以在和特征矩阵$H$ 乘的时候，只会计算一个node的所有邻居的特征的加权和，该node自己的特征却被忽略了。因此，做了一个小小的改动，给$A$ 上一个单位矩阵$I$，这样就让对角线元素变成1了。

（2）$A$ 没有经过归一化的矩阵，这样与特征矩阵相乘会改变特征原本的分布，产生一些不可预测的问题。所以我们对$A$ 一个标准化处理。首先让$A$ 每一行加起来为1，我们可以乘以一个$D^{-1}$ ，$D$ 是度矩阵。考虑每一列做到归一化，所以我们可以进一步把$D^{-1}$ 拆开与A相乘，得到一个对称且归一化的矩阵$D^{\frac{-1}{2}}A{D}^{\frac{-1}{2}}$。此设计与对称归一化拉普拉斯矩阵十分类似，而在谱图卷积的核心就是使用对称归一化拉普拉斯矩阵，这也是GCN的卷积叫法的来历。（具体的我也不懂，只知道是这样，从而说明了谱域的图卷积是空域图卷积的子集。)

通过对上面两个局限的改进，我们便得到了最终的层特征传播公式：

$$f(H^{(l)},A)=\sigma ({\hat{D}}^{\frac{-1}{2}}\hat{A}{\hat{D}}^{\frac{-1}{2}}{H}^{(l)}{W}^{(l)})$$

三、Example

下面用一个例子记录GCN强大公式是如何起作用的。

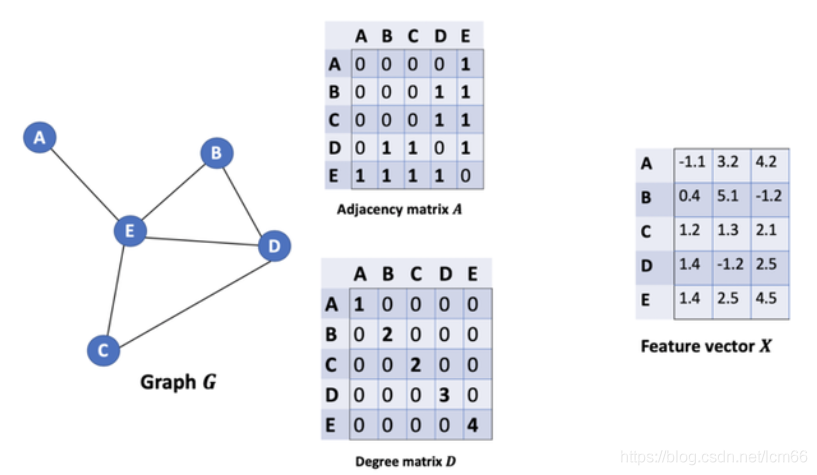
【引用：https://baijiahao.baidu.com/s?id=1678519457206249337&wfr=spider&for=pc】

直接将矩阵$A$ 矩阵$X$ 乘，得到的矩阵第一行就是与$A$ 连接的$E$ 点的特征向量（如下图）。同理，得到的矩阵的第二行是D和E的特征向量之和，通过这个方法，我们可以得到所有邻居节点的向量之和。

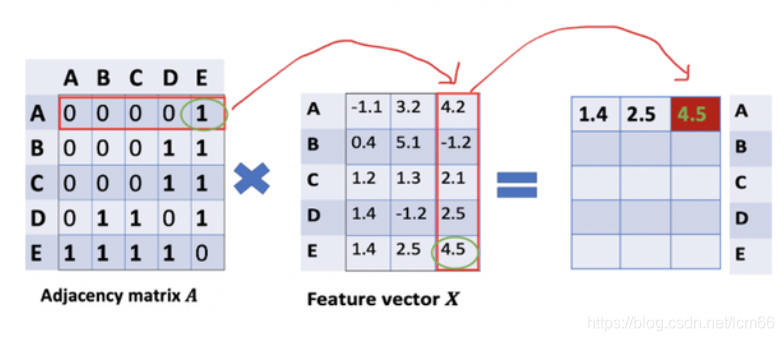
此时的计算还存在上述章节三中提到的局限（1）忽略了节点本身的特征。按理得到的矩阵第一行应该包含结点A和E的信息，所以做出改进：

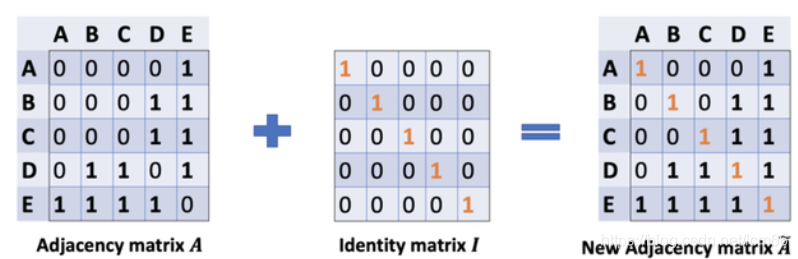
通过给每个节点增加一个自循环，我们得到新的邻接矩阵。

对于局限（2）矩阵缩放，实现归一化。

在矩阵缩放中，通常考虑乘上一个对角矩阵，正好度矩阵$D$ 对角矩阵，一定存在这某种关联，所以有了如下的改进：

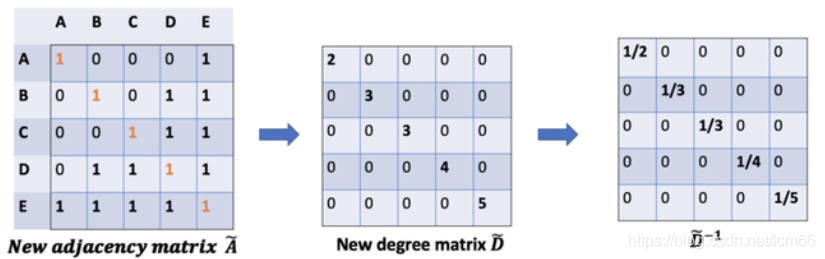
因此，通过$D$ 反和$X$ 乘法，我们可以取所有邻居节点的特征向量（包括自身节点）的平均值。

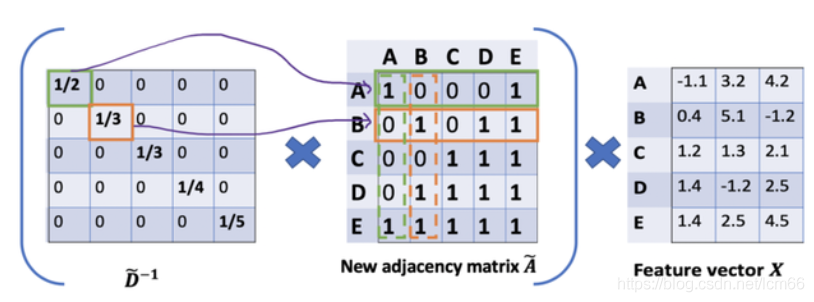
按照上图左乘一个D波浪逆矩阵，我们只是按行缩放(即，行归一化)，而忽略了对应的列（虚线框）。【缩放方法给我们提供了 "加权 "的平均值。我们在这里做的是给低度的节点加更多的权重，以减少高度节点的影响。这个加权平均的想法是，我们假设低度节点会对邻居节点产生更大的影响，而高度节点则会产生较低的影响，因为它们的影响力分散在太多的邻居节点上。】

所以，进行了两次归一化处理，左乘和右乘了$\tilde{D}$ -1/2逆。

$$f(H^{(l)},A)=\sigma ({\hat{D}}^{\frac{-1}{2}}\hat{A}{\hat{D}}^{\frac{-1}{2}}{H}^{(l)}{W}^{(l)})$$

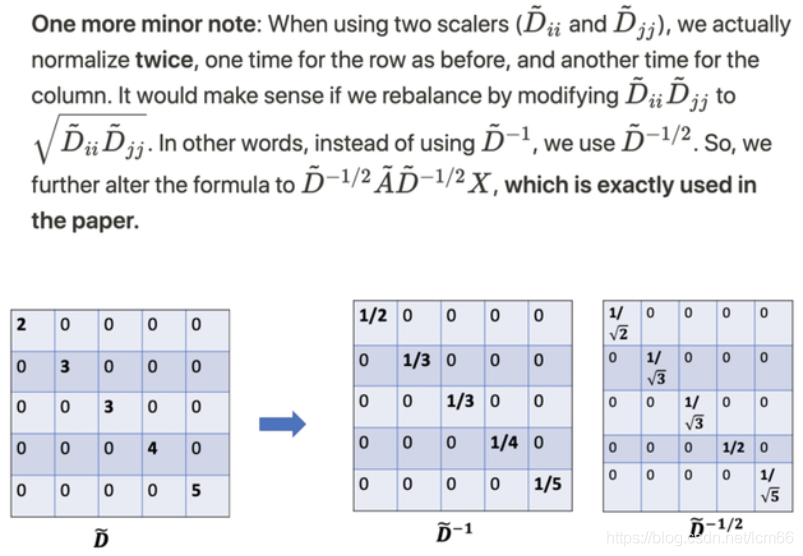
至此，强大的GCN公式诞生。

四、Others

1. 对于很多网络，我们可能没有节点的特征，这个时候可以使用GCN吗？答案是可以的，如论文中作者对那个俱乐部网络，采用的方法就是用单位矩阵 $ I $ 替换特征矩阵 $X$。
2. 我没有任何的节点类别的标注，或者什么其他的标注信息，可以使用GCN吗？当然，就如前面讲的，不训练的GCN，也可以用来提取graph embedding，而且效果还不错。
3. GCN网络的层数多少比较好？论文的作者做过GCN网络深度的对比研究，在他们的实验中发现，GCN层数不宜多，2-3层的效果就很好了。
4. GCNs同时使用节点特征和结构进行训练。
5. 该框架目前仅限于无向图（加权或不加权）。但是，可以通过将原始有向图表示为一个无向的两端图，并增加代表原始图中边的节点，来处理有向边和边特征。

References

GCN (Graph Convolutional Network) 图卷积网络解析_祥瑞的技术博客-CSDN博客_图卷积网络 (opens new window)

GCN——初步理解_AiA_AiA的博客-CSDN博客 (opens new window)

https://www.zhihu.com/question/54504471/answer/332657604