随机变量及其分布

随机变量的概念

1. 随机变量（Random variable） ：值随机会而定的变量，研究随机试验的一串事件。可按维数分为一维、二维至多维随机变量。按性质可分为离散型随机变量以及连续型随机变量。
2. 分布（Distribution） ：事件之间的联系，用来计算概率。
3. 示性函数（Indication function） ：$I_A(\omega )=\{\begin{array}{ll}1& \omega \in A\\ 0& \text{ 反之}\end{array}$，事件$A$ 随机变量$I_A$ 示出来，$I_A$ 为事件$A$ 示性函数。

离散型随机变量及其分布

1. 离散型随机变量 ：设$X$ 一随机变量，如果$X$只取有限个或可数个值，则称$X$ 一个（一维）离散型随机变量。

2. 概率函数 ：设$X$ 一随机变量，其全部可能值为$\{a_1,a_2,...\}$，则$p_i=P(X=a_i),i=1,2,...$ 为$X$ 概率函数。

3. 概率分布 ：离散型随机变量的概率分布可以用分布表来表示：

   可能值	$a_1$	$a_2$	...	$a_i$	...
   概率	$p_1$	$p_2$	...	$p_i$	...

4. 概率分布函数 ：

   • 定义 ：设$X$ 一随机变量，则函数

$$F(X)=P(X\le x)(-\mathrm{\infty }<x<\mathrm{\infty })$$

称为$X$ 分布函数。（注：这里并未限定$X$ 离散型的，它对任何随机变量都有定义。）

• 性质 ：

  • $F(x)\mathrm{是}\mathrm{单}\mathrm{调}\mathrm{非}\mathrm{降}\mathrm{的}：\mathrm{当}$$x_1<x_2$ ，有$F(x_1)\le F(X_2)$.
  • 当$x\to \mathrm{\infty }$ ，$F(x)\to 1$；当$x\to -\mathrm{\infty }$ ，$F(x)\to 0$.

• 离散型随机变量分布函数 ：

  对于离散型随机变量，$F(X)=P(X\le x)=\sum _{\{i|a_i\le x\}}{p}_i,p_i=P(X=i)=F(i)-F(i-1)$。

5. 二项分布（Bionomial distribution）：

   • 定义 ：设某事件$A$ 一次试验中发生的概率为$p$，先把试验独立地重复n次，以$X$ $A$ 这n次试验中发生的次数，则$X$ 值$0,1,...,n$，且有

     $$P(X=k)=(\genfrac{}{}{0ex}{}{n}{k})p^k(1-p{)}^{n-k},k=0,1,...,n$$

     称$X$ 从二项分布，记为$X\sim B(n,p)$.

   • 服从二项分布的条件 ：1. 各次试验的条件是稳定的，即事件$A$ 概率$p$ 各次试验中保持不变；2. 各次试验的独立性

6. 泊松分布（Poisson distribution） ：

   • 定义 ：设随机变量$X$ 概率分布为

     $$P(X=i)=\frac{{\lambda }^i}{i!}{e}^{-\lambda },i=0,1,2,...,\lambda >0$$

     则称$X$ 从参数为$\lambda$ Poisson分布，并记$X\sim P(\lambda )$.

   • 特点 ：

     • 描述稀有事件发生概率

     • 作为二项分布的近似。若$X\sim B(n,p)$，其中$n$ 大，$p$ 小，而$np=\lambda$ 太大时（一般$n>30,np\le 5$），则$X$ 分布接近泊松分布$P(\lambda )$.

       推导 ：

       若事件$A\sim B(n,p)$，且$n$ 大，$p$ 小，而$np=\lambda$ 太大时，设$\lambda =np$，

       $$\begin{array}{rl}P(X=i)& =\underset{n\to \mathrm{\infty }}{lim}(\genfrac{}{}{0ex}{}{n}{i})(\frac{\lambda }{n}{)}^i(1-\frac{\lambda }{n}{)}^{n-i}\\ & ={\lambda }^i\underset{n\to \mathrm{\infty }}{lim}\frac{(\genfrac{}{}{0ex}{}{n}{i})}{n^i}\underset{n\to \mathrm{\infty }}{lim}(1-\frac{\lambda }{n}{)}^{n-i}\\ & ={\lambda }^i{e}^{-\lambda }\underset{n\to \mathrm{\infty }}{lim}\frac{n(n-1)(n-2)...(n-i+1)}{i!n^i}\\ & ={\lambda }^i{e}^{-\lambda }\underset{n\to \mathrm{\infty }}{lim}\frac{(1-\frac{1}{n})(1-\frac{2}{n})...(1-\frac{i-1}{n})}{i!}\\ & =\frac{{\lambda }^i}{i!}{e}^{-\lambda }\end{array}$$

连续型随机变量及其分布

1. 连续型随机变量 ：设$X$ 一随机变量，如果$X$不仅有无限个而且有不可数个值，则称$X$ 一个连续型随机变量。

2. 概率密度函数 ：

   • 定义 ：设连续型随机变量$X$ 概率分布函数$F(x)$，则$F(x)$ 导数$f(x)=F^{\prime }(x)$ 为$X$ 概率密度函数。

   • 性质 ：

     • 对于所有的$-\mathrm{\infty }<x<+\mathrm{\infty }$，有$f(x)\ge 0$；
     • ${\int }_{-\mathrm{\infty }}^{+\mathrm{\infty }}f(x)dx=1$；
     • 对于任意的$-\mathrm{\infty }<a\le b<+\mathrm{\infty }$，有$P(a\le X\le b)=F(b)-F(a)={\int }_a^{b}f(x)dx$.

   • 注 ：

     • 对于任意的$-\mathrm{\infty }<x<+\mathrm{\infty }$，有$P(X=x)={\int }_x^{x}f(u)du=0$.
     • 假设有总共一个单位的质量连续地分布在$a\le x\le b$ ，那么$f(x)$ 示在点$x$ 质量密度且${\int }_c^{d}f(x)dx$ 示在区间$[c,d]$ 的全部质量。

3. 概率分布函数 ：设$X$ 一连续型随机变量，则

   $$F(x)={\int }_{-\mathrm{\infty }}^{x}f(u)du,-\mathrm{\infty }<x<+\mathrm{\infty }$$

4. 正态分布（Normal distribution） ：

   • 定义 ：如果一个随机变量具有概率密度函数

     $$f(x)=\frac{1}{\sqrt{2\pi }\sigma }{e}^{-\frac{(x-\mu {)}^2}{2{\sigma }^2}},-\mathrm{\infty }<x<+\mathrm{\infty }$$

     其中$-\mathrm{\infty }<\mu <+\mathrm{\infty },{\sigma }^2>0$，则称$X$ 正态随机变量，并记为$X\sim N(\mu ,{\sigma }^2)$.特别地，$\mu =0,\sigma =1$ 正态分布成为标准正态分布。用$\mathrm{\Phi }(x)$ $\varphi (x)$ 示标准正态分布$N(0,1)$ 分布函数和密度函数。

   • 性质 ：

     • 正态分布的密度函数是以$x=\mu$ 对称轴的对称函数，$\mu$ 为位置参数，密度函数在$x=\mu$ 达到最大值，在$(-\mathrm{\infty },\mu )$ $(\mu ,+\mathrm{\infty })$ 严格单调。
     • $\sigma$ 大小决定了密度函数的陡峭程度，通常称$\sigma$ 正态分布的形状参数。
     • 若$X\sim N(\mu ,{\sigma }^2)$，则$Y=(X-\mu )/\sigma \sim N(0,1)$.
     • $\mathrm{\Phi }(-k)=1-\mathrm{\Phi }(k)$

   • 图像（密度和分布函数图） ：

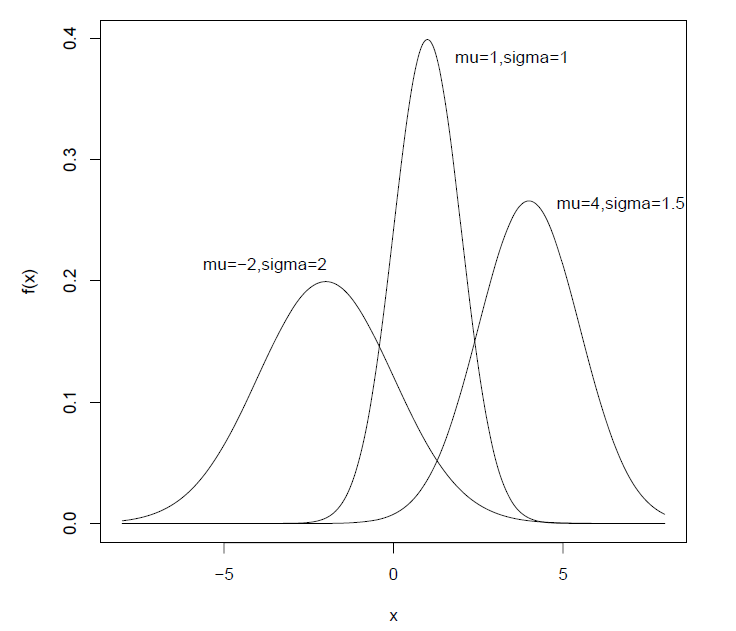
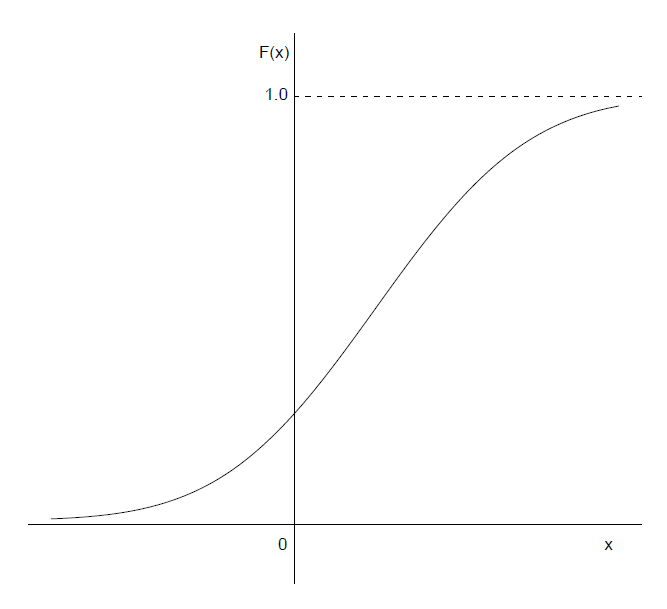
4. 指数分布（Exponential distribution） ：

   • 定义 ：若随机变量$X$ 有概率密度函数

     $$f(x)=\{\begin{array}{ll}\lambda e^{-\lambda x}& x>0\\ 0& x\le 0\end{array}=\lambda e^{-\lambda x}{I}_{(0,\mathrm{\infty })}(x)$$

     其中$\lambda >0$ 常数，则称$X$ 从参数为$\lambda$ 指数分布。

   • 概率分布函数 ：$F(x)=\{\begin{array}{ll}1-e^{-\lambda x}& x>0\\ 0& x\le 0\end{array}=(1-e^{-\lambda x})I_{(0,\mathrm{\infty })}(x)$

   • 性质 ：

     • 无后效性，即无老化，要来描述寿命（如元件等）的分布。

       证明 ：

       “无老化”就是说在时刻$x$ 常工作的条件下，其失效率总保持为某个常数$\lambda >0$，与$x$ 关，可表示

       $$\begin{array}{rl}& P(x\le X\le x+h|X>x)/h=\lambda (h\to 0)\\ \mathrm{证}：\\ & \underset{h\to 0}{lim}\frac{P(x\le X\le x+h|X>x)}{h}\\ =& \underset{h\to 0}{lim}\frac{P(x\le X\le x+h,X>x)}{P(X>x)h}\\ =& \underset{h\to 0}{lim}\frac{P(x<X\le x+h)}{P(X>x)h}\\ =& \underset{h\to 0}{lim}\frac{-e^{-\lambda t}{|}_x^{x+h}}{-e^{-\lambda t}{|}_x^{\mathrm{\infty }}h}\\ =& \underset{h\to 0}{lim}\frac{e^{-\lambda x}-e^{-\lambda x-\lambda h}}{e^{-\lambda x}h}\\ =& \underset{h\to 0}{lim}\frac{1-\frac{1}{e^{xh}}}{h}\\ =& \underset{h\to 0}{lim}\lambda e^{-\lambda h}\\ =& \lambda \end{array}$$

     • $\lambda$ 失效率，失效率越高，平均寿命就越小。

   • 图像（密度函数） ：

     

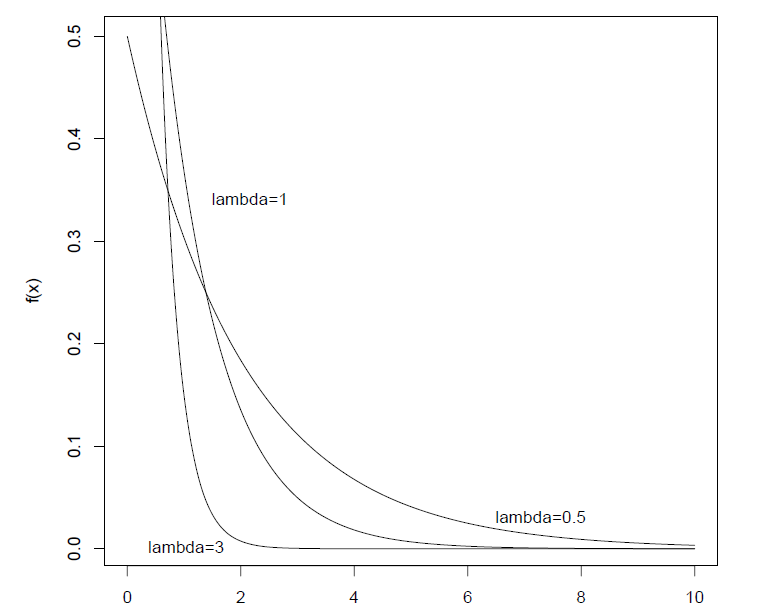
5. 均匀分布（Uniform distribution） ：

   • 定义 ：设$a<b$，如果分布$F(x)$ 有密度函数

     $$f(x)=\{\begin{array}{ll}\frac{1}{b-a}& a\le x\le b\\ 0& \mathrm{其}\mathrm{它}\end{array}=\frac{1}{b-a}{I}_{(a,b)}(x)$$

     则该分布为区间$[a,b]$ 的均匀分布。

   • 概率分布函数 ：$F(x)=\{\begin{array}{ll}0& x\le a\\ \frac{x-a}{b-a}& a<x\le b\\ 1& x>b\end{array}$

   • 性质 ：$\mathrm{\forall }R(c,d)\subset R(a,b),P(c<X<d)=\frac{d-c}{b-a}$

多维随机变量（随机向量）

1. 随机向量 ：设$X=\{X_1,...,X_n\}$.如果每个$X_i$ 是一个随机变量，$i=1,...,n$，则称$X$ $n$ 随机变量或者随机向量。

2. 离散型随机向量的分布 ：如果每一个$X_i$ 是一个离散型随机变量，$i=1,...,n$，则称$X=\{X_1,...,X_n\}$ 一$n$ 离散型随机变量。设$X_i$ 所有可能取值为$\{a_{i1},ai2,...\},i=1,...,n$，则称

   $$p(j_1,...,j_n)=P(X_1=a_{1j_1},...,X_n=a_{n{j}_n}),j_1,...,j_n=1,2,...$$

   为$n$ 随机变量$X$ 概率函数，这也是其联合分布。

   其具有下列性质：

   • $p(j_1,...,j_n)\ge 0,j_i=1,2,...,i=1,2,...,n;$
   • $\sum _{j_1,...,j_n}p(j_1,...,j_n)=1.$

   注 ：对于高维离散型随机变量，一般不使用分布函数

3. 多项式分布

   • 定义 ：设$A_1,A_2,...,A_n$ 某一试验之下的完备事件群，分别以$p_1,p_2,...,p_n$ 事件$A_1,A_2,...,A_n$ 概率，则$p_i\ge 0,p_1+...+p_n=1$.将试验独立地重复$N$ ，以$X_i$ 在这$N$ 试验中事件$A_i$ 现的次数$(i=1,...,n)$，则$X=(X_1,...,X_n)$ 一个$n$ 随机向量。该分布记作$M(N;p_1,...,p_n)$.

   • 概率分布函数 ：$P(X_1=k_1,X_2=k_2,...,X_n=k_n)=\frac{N!}{k_1!k_2!...k_n!}{p}_1^{k_1}{p}_2^{k_2}....p_n^{k_n}$

4. 连续型随机向量的分布 ：$X=\{X_1,...,X_n\}$ $n$ 连续型随机变量，如果存在${\text{R}}^n$ 的非负函数$f(x_1,...,x_n)$，使得对任意的$-\mathrm{\infty }<a_1\le b_1<+\mathrm{\infty },...,-\mathrm{\infty }<a_n\le b_n<+\mathrm{\infty }$，有

   $$P(a_1\le X_1\le b_1,...,a_n\le X_n\le b_n)={\int }_{a_n}^{b_n}...{\int }_{a_1}^{b_1}f(x_1,...,x_n)d{x}_1...d{x}_n$$

   则称为$f$ $X$ 概率密度函数。有

   $$P(a_1\le X_1\le b_1,...,a_n\le X_n\le b_n)=F(x_1,...,x_n)$$

   则称为$F$ $X$ （联合）分布函数。其中分布函数$F(X_1,...,X_n)$ 有下述性质：

   • $F(x_1,...,x_n)$ 调非降；
   • 对任意的$1\le j\le n$，有$\underset{x_j\to -\mathrm{\infty }F(x_1,...,x_n)}{lim}=0$；
   • $\underset{x_1\to \mathrm{\infty },...,x_n\to \mathrm{\infty }}{lim}F(x_1,...,x_n)=1$

5. 边缘分布 ：因为$X$ 每个分量$X_i$ 是一维随机变量，故它们都有各自的分布$F_i(i=1,...,n)$，这些都是一维分布，称为随机向量$X$ 其分布$F$ 边缘分布。

   • 离散型随机向量

     

     行和与列和就是边缘分布。即固定某个$x_i$，即可计算边缘分布，故有

     $$\begin{gathered} p_X(x_i)=P(X=x_i)=\sum _j^{m}P(X=x_i,Y=y_j)=\sum _j^m{p}_{ij}=p_{i\cdot },i=1,2,...,n \\ {p}_Y(y_i)=P(Y=y_i)=\sum _i^{m}P(X=x_i,Y=y_j)=\sum _i^m{p}_{ij}=p_{j\cdot },j=1,2,...,n \end{gathered}$$

   • 连续型随机向量

     为求某分量$X_i$ 概率密度函数，只需把$f(x_1,...,x_n)$ 的$x_i$ 定，然后对$x_1,...,x_{i-1},x_{i+1},...,x_n$ $-\mathrm{\infty }$ $\mathrm{\infty }$ 间做定积分，如

     $$\begin{gathered} (X,Y)\sim f(x,y) \\ {f}_X(u)={\int }_{-\mathrm{\infty }}^{+\mathrm{\infty }}f(u,v)dv \\ {f}_Y(u)={\int }_{-\mathrm{\infty }}^{+\mathrm{\infty }}f(u,v)du \end{gathered}$$

注 ：二维正态分布$N(a,b,{\sigma }_1^2,{\sigma }_2^2,\rho )$ 边缘分布密度分别是一维正态分布$N(a,{\sigma }_1^2)$ $N(b,{\sigma }_2^2)$。因此联合分布可推边缘分布，而边缘分布不可推联合分布。

条件分布和随机变量的独立性

1. 离散型随机变量的条件分布 ：设$(X,Y)$ 二维离散型随机变量，对于给定的事件$\{Y=y_j\}$，其概率$P(Y=y_j)>0$，则称

   $$P(X=x_i|Y=y_j)=\frac{P(X=x_i,Y=y_j)}{P(Y=y_j)}=\frac{p_{ij}}{p_{\cdot j}},i=1,2,...$$

   为在给定$Y=y_j$ 条件下$X$ 条件分布律。类似的，称

   $$P(Y=y_i|X=x_j)=\frac{P(X=x_i,Y=y_j)}{P(X=x_j)}=\frac{p_{ij}}{p_{i\cdot }},j=1,2,...$$

   为在给定$X=x_j$ 条件下$Y$ 条件分布律。

2. 连续型随机变量的条件分布 ：设$(X,Y)$ 二维连续型随机变量，对于给定条件$Y=y$ 的条件概率密度为

   $$f_{X|Y}(x|y)=\frac{f(x,y)}{f_Y(y)},f_Y(y)>0.$$

   类似的，在$X=x$ 的条件概率密度为

   $$f_{Y|X}(y|x)=\frac{f(x,y)}{f_X(x)},f_X(x)>0.$$

   二维正态分布$\rho =0$ ，其联合密度分布等于条件密度分布的乘积。

3. 随机变量的独立性

   称随机变量$X_1,...,X_n$ 互独立，

   • 离散型随机变量

     则联合分布律等于各自的边缘分布律的乘积，即

     $$P(X_1=x_1,...,X_n=x_n)=P(X_1=x_1)...P(X_n=x_n)$$

     其中$(x_1,...x_n)$ $(X_1,...,X_n)$ 值域中的任意一点。

   • 连续型随机变量

     则联合密度等于各自的边缘密度的乘积，即

     $$f(x_1,...,x_n)=f_1(x_1)...f_n(x_n),\mathrm{\forall }(x_1,...,x_n)\in {\text{R}}^n$$

   • 更具一般地

     设$X_1,...,X_n$ $n$ 随机变量，如果它们的联合分布函数等于各自边缘分布函数的乘积，即

     $$F(X_1,...,x_n)=F_1(x_1)...F_n(x_n),\mathrm{\forall }(x_1,...,x_n)\in {\text{R}}^n$$

     则称随机变量$X_1,...,X_n$ 互独立。

   一些重要的结论

   

随机变量的函数的概率分布

  最简单的情形，是由一维随机变量$X$ 概率分布去求其一给定函数$Y=g(X)$ 分布。较为常见的，是由$(X_1,X_2,...,X_n)$ 分布去求$Y=g(X_1,X_2,...,X_n)$ 分布。更一般地，由$(X_1,X_2,...,X_n)$ 分布去求$(Y_1,Y_2,...,Y_m)$ 分布，其中$Y_i=g_i(X_1,X_2,...,X_n),i=1,2,...,m$.

1. 离散型分布的情形 ：设$X$ 分布律为$P(X=x_i)=p_i,i=1,2,...$

   $g:R\to R$，令$Y=g(X)$，则$Y$ 分布律为

   $$P(Y=y_j)=P(g(X)=y_j)=\sum _{x_i:g(x_i)=y_j}P(X=x_i)=\sum _{i:g(x_i)=y_j}{p}_i$$

   即把$Y=g(X_1,...,X_n)$ 以取的不同值找出来，把与某个值相应的全部$(X_1,...,X_n)$ 的概率加起来，即得$Y$ 这个值的概率。

2. 连续型分布的情形

   • 一个变量的情况

     设$X$ 密度函数$f(x)$.设$Y=g(x)$，$g$ 一个严格单调的函数，即当$x_1<x_2$ ，必有$g(x_1)<g(x_2)$ 当$x_1>x_2$ ，必有$g(x_1)>g(x_2)$.又设$g$ 导数$g^{\prime }$ 在。由于$g$ 严格单调性，其反函数$X=h(Y)$ 在，且$h$ 导数$h^{\prime }$ 存在。有$g(X)$ 密度函数$l(y)$

     $$l(y)=f(h(y))|h^{\prime }(y)|.$$

   • 多个变量的情形

     以两个为例，设$(X_1,X_2)$ 密度函数$f(x_1,x_2)$，$Y_1,Y_2$ 是$(X_1,X_2)$ 函数：

     $$Y_1=g_1(X_1,X_2),Y_2=g_2(X_1,X_2),$$

     要求$(Y_1,Y_2)$ 概率密度函数$l(y_1,y_2)$.假定$(X_1,X_2)$ $(Y_1,Y_2)$ 一一对应变换有逆变换：

     $$X_1=h_1(Y_1,Y_2),X_2=h_2(Y_1,Y_2)$$

     即雅可比行列式

     $$J(y_1,y_2)=\left|\begin{array}{cc}\partial h_1/\partial y_1& \partial h_1/\partial y_2\\ \partial h_2/\partial y_1& \partial h_2/\partial y_2\end{array}\right|$$

     不为0.在$(Y1,Y2)$ 平面上任取一个区域$A$，变换后到$(X_1,X_2)$ 面的区域$B$，则有

     $$\begin{gathered} P((Y_1,Y_2)\in A)=P((X_1,X_2)\in B)={\iint }_{B}f(x_1,x_2)d{x}_{1}d{x}_2 \\ P((Y_1,Y_2)\in A)={\iint }_{A}f(h_1(y_1,y_2),h_2(y_1,y_2))|J(y_1,y_2)|d{y}_{1}d{y}_2 \end{gathered}$$

   • 随机变量和的密度函数

     设$(X_1,X_2)$ 联合密度函数为$f(x_1,x_2)$，$Y=X_1+X_2$ 密度函数：

     • 一般的，$l(y)={\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}f(x_1,y-x_1)d{x}_1={\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}f(x,y-x)dx$.
     • 若$X_1,X_2$ 立，则$l(y)={\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}{f}_1(x)f_2(y-x)dx={\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}{f}_1(y-x)f_2(x)dx$.

     两个独立的正态变量的和仍服从正态分布，且有关的参数相加，其逆命题也成立。

   • 随机变量商的密度函数 设$(X_1,X_2)$ 联合密度函数为$f(x_1,x_2)$，$Y=X_1/X_2$ 密度函数：

     • 一般的，$l(y)={\int }_0^{\mathrm{\infty }}{x}_{1}f(x_1,x_{1}y)d{x}_1$.
     • 若$X_1,X_2$ 立，则$l(y)={\int }_0^{\mathrm{\infty }}{x}_1{f}_1(x_1)f_2(x_{1}y)d{x}_1$.

• 统计学三大分布

  引入两个重要的特殊函数：

  $\mathrm{\Gamma }(x)={\int }_0^{\mathrm{\infty }}{e}^{-t}{t}^{x-1}dt(x>0)$ 和 $B(x,y)={\int }_0^1{t}^{x-1}(1-t{)}^{y-1}dt(x>0,y>0)$

  其中，$\mathrm{\Gamma }(1)=1,\mathrm{\Gamma }(1/2)=\sqrt{\pi },\mathrm{\Gamma }(n)=(n-1)!$

  $B(x,y)=\mathrm{\Gamma }(x)\mathrm{\Gamma }(y)/\mathrm{\Gamma }(x+y)$

  • 卡方分布，记作${\chi }_n^2$

    密度函数 ：$k_n(x)=\frac{1}{\mathrm{\Gamma }(\frac{n}{2}{2}^{n/2})}{e}^{-x/2}{x}^{(n-2)/2}{I}_{(0,\mathrm{\infty })}(x)$

    性质 ：1. 设$X_1,X_2$ 立，$X_1\sim {\chi }_m^2,X_2\sim {\chi }_n^2$，则$X_1+X_2\sim {\chi }_{m+n}^2$

    ​ 2. 若$X_1,...,X_n$ 立，且都服从指数分布，则$X=2\lambda (X_1+...+X_n)\sim {\chi }_{2n}^2$

  • $t$ 布，记作$t_n$

    设$X_1，X_2$ 立，$X_1\sim {\chi }_n^2,X_2\sim N(0,1)$，而$Y=X_2/\sqrt{X_1/n}$，则$Y\sim t_n$.

    密度函数 ：$t_n(y)=\frac{\mathrm{\Gamma }((n+1)/2)}{\sqrt{n\pi }\mathrm{\Gamma }(n/2)}(1+\frac{y^2}{n}{)}^{(\frac{n+1}{2})}$

    性质 ：密度函数关于原点对称，其图形与正态分布$N(0,1)$ 密度函数的图形相似。

  • $F$ 布，记作$F_{mn}$

    设$X_1,X_2$ 立，$X_1\sim {\chi }_n^2,X_2\sim {\chi }_m^2$，而$Y=m^{-1}{X}_2/(n^{-1}{X}_1)$，则$Y\sim F_{mn}$

    密度函数 ：$f_{mn}(y)=m^{m/2}{n}^{n/2}\frac{\mathrm{\Gamma }(\frac{m+n}{2})}{\mathrm{\Gamma }(\frac{m}{2})\mathrm{\Gamma }(\frac{n}{2})}{y}^{m/2-1}(my+n{)}^{-(m+n)/2}(y>0)$

  三大分布的几个重要性质

  1. 设$X_1,...,X_n$ 立同分布，有公共的正态分布$N(\mu ,{\sigma }^2)$.记$\overline{X}=(X_1+...+X_n),S^2=\sum _{i=1}^n(X_i-\overline{(}X){)}^2/(n-1)$.则$(n-1)S^2/{\sigma }^2=\sum _{i=1}^n(X_i-\overline{X}{)}^2/{\sigma }^2\sim {\chi }_{n-1}^2$.

  2. 设$X_1,...,X_n$ 假定同1，则$\sqrt{n}(\overline{X}-\mu )/S\sim t_{n-1}$

  3. 设$X_1,...,X_n,Y_1,...,Y_m$ 立，$X_i$ 有分布$N(\mu 1,{\sigma }_1^2)$，$Y_j$ 有分布$N({\mu }_2,{\sigma }_2^2)$，则

     $$[\sum _{j=1}^m(Y_j-\overline{Y}{)}^2/({\sigma }_2^2(m-1))]/[\sum _{i=1}^n(X_i-\overline{X}{)}^2/({\sigma }_1^2(n-1))]\sim F_{m-1,n-1}$$

     若${\sigma }_1^2={\sigma }_2^2$，则

     $$\sqrt{\frac{nm(n+m-2)}{n+m}}[(\overline{X}-\overline{Y})-({\mu }_1-{\mu }_2)]/[\sum _{i=1}^n(X_i-\overline{X}{)}^2+\sum _{j=1}^m(Y_j-\overline{Y}{)}^2{]}^{1/2}\sim t_{n+m-2}$$