统计量及其分布

总体与样本

1. 总体

     在一个统计问题里，研究对象的全体叫做总体，构成总体的每个成员称为个体。根据个体的数量指标数量，定义总体的维度，如每个个体只有一个数量指标，总体就是一维的，同理，个体有两个数量指标，总体就是二维的。总体就是一个分布，数量指标就是服从这个分布的随机变量。   总体根据个体数分为有限总体和无限总体，当有限总体的个体数充分大时，其可以看为无限总体。

2. 样本

   • 定义：

     从总体中随机抽取的部分个体组成的集合称为样本，样本个数称为样本容量。

   • 性质：

     • 二重性：抽取前随机，是随机变量；抽取后确定，是一组数值。

     • 随机性：每个个体都有同等的机会被选入样本。

   • 独立性：每个样本的取值不影响其他样本取值，即分部独立。

     满足后面两个性质称为简单随机样本，则

     $$\begin{gathered} F(x_1,x_2,...,x_n)=\prod _{i=1}^{n}F(x_i), \\ f(x_1,x_2,...,x_n)=\prod _{i=1}^{n}f(x_i), \\ p(x_1,x_2,...,x_n)=\prod _{i=1}^{n}p(x_i) \end{gathered}$$

3. 分组样本

     只知样本观测值所在区间，而不知具体值的样本称为分组样本。缺点：与完全样本相比损失部分信息。优点：在样本量较大时，用分组样本既简明扼要，又能帮助人们更好地认识总体。

样本数据的整理与显示

1. 经验分布函数

     若将样本观测值$x_1,x_2,...,x_n$ 小到大进行排列，得到有序样本$x_{(1)}\le x_{(2)}\le ...\le x_{(n)}$，用有序样本定义如下函数

   $$F_n(x)=\{\begin{array}{cc}0& \mathrm{当}x<x_{(1)}\\ k/n& \mathrm{当}{x}_{(k)}\le x<x_{(k+1)},k=1,2,...,n-1\\ 1& \mathrm{当}x\ge x_{(n)}\end{array}$$

   则称为$F_n(x)$ 该样本的经验分布函数。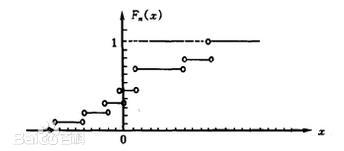

   

2. 格里纹科定理

     设$x_1,x_2,...,x_n$ 取自总体分布函数为$F(x)$ 样本，$F_n(x)$ 该样本的经验分布函数，则当$n\to +\mathrm{\infty }$ ，有

   $$P(su{p}_{-\mathrm{\infty }<x<+\mathrm{\infty }}|F_n(x)-F(x)|\to 0)=1$$

   表明当 n 相当大时，经验分布函数$F_n(x)$ 总体分布函数$F(x)$ 一个良好的近似。它是经典统计学的一块基石。

3. 频数频率分布表

     有样本$x_1,x_2,...,x_n$ 作频数频率分布表的操作步骤如下：

   • 确定组数 k；
   • 确定每组组距，通常取每组组距相等为 d（方便起见，可选为整数）；
   • 确定组限（下限$a_0$ 小于最小观测值，上限$a_k$ 大于最大观测值）；
   • 统计样本数据落入每个区间的频数，并计算频率。

   该表能够简明扼要地把样本特点表示出来。不足之处是该表依赖于分组，不同的分组方式有不同的频数频率分布表。

   

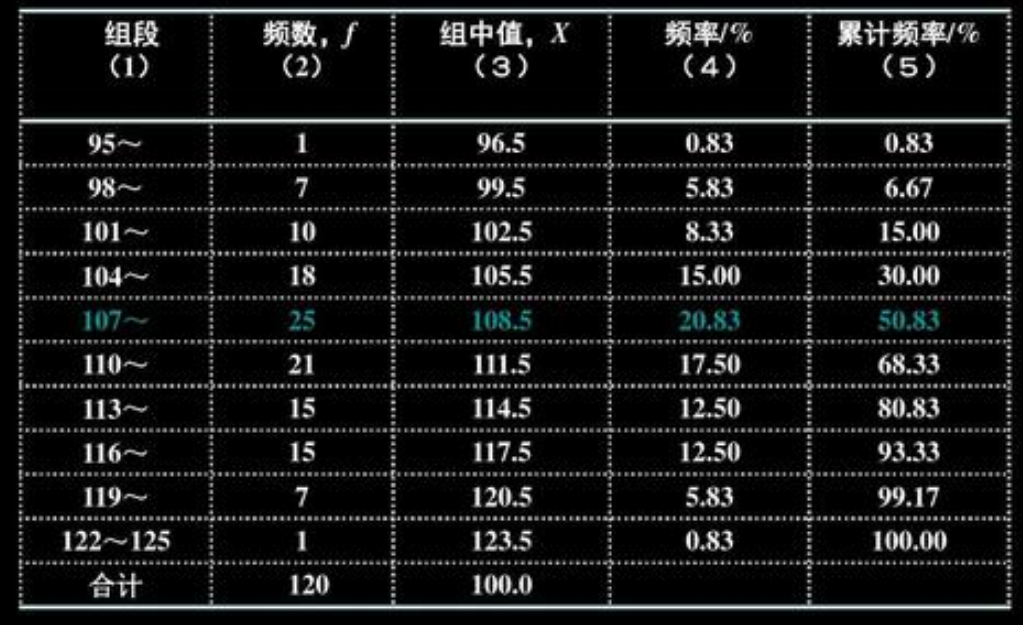
4. 直方图

   • 利用频数频率分布表上的区间（横坐标）和频数（纵坐标）可作为频数直方图；
   • 若把纵坐标改为频率就得频率直方图；
   • 若把纵坐标改为频率/组距，就得到单位频率直方图。这时长条矩形的面积之和为 1.
   

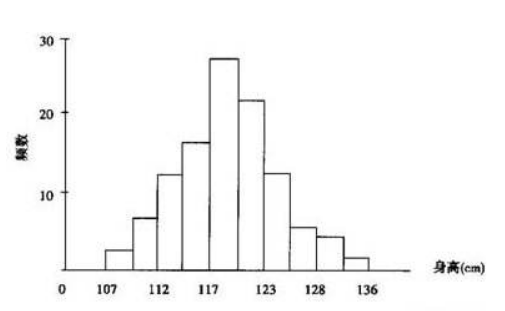
5. 茎叶图

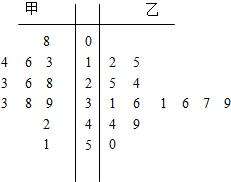
     把样本中的每个数据分为茎与叶，把茎放于一侧，叶放于另一侧，就得到一张该样本的茎叶图。比较两个样本时，可画出背靠背的茎叶图。茎叶图保留数据中全部信息，当样本量较大，数据很分散，横跨二、三个数量级时，茎叶图并不适用。

   

统计量及其分布

1. 统计量

     不含未知参数的样本函数称为统计量。统计量的分布称为抽样分布。

2. 样本均值

   • 定义：

       样本$x_1,x_2,...,x_n$ 算数平均值称为样本均值，记为$\overline{x}$.分组样本均值$\overline{x}=\frac{1}{n}\sum _{i=1}^k{x}_i{f}_i$，其中 n 为样本量，k 为组数，$x_i$ $f_i$ 第 i 组的组中值和频率，分组样本均值是完全样本均值的一种较好的近似。

       样本均值是样本的位置特征，样本中大多数值位于$\overline{x}$ 右。平均可消除一些随机干扰，等价交换也是在平均数中实现的。

   • 性质：

     • $\sum _{i=1}^n(x_i-\overline{x})=0$，样本数据$x_i$ 样本均值$\overline{x}$ 偏差之和为零；
     • 样本数据$x_i$ 样本均值$\overline{x}$ 偏差平方和最小，即对任意的实数 c 有$\sum _{i=1}^n(x_i-\overline{x}{)}^2\le \sum _{i=1}^n(x_i-c{)}^2$;
     • 若总体分布为$N(\mu ,{\sigma }^2)$，则$\overline{x}$ 精确分布为$N(\mu ,{\sigma }^2/n)$；
     • 若总体分布未知，但其期望$\mu$ 方差${\sigma }^2$ 在，则当 n 较大时，$\overline{x}$ 渐进分布为$N(\mu ,{\sigma }^2/n)$，这里渐进分布是指 n 较大时的近似分布。

3. 样本方差与样本标准差

     样本方差有两种，$s_{\ast }^2=\frac{1}{n}\sum _{i=1}^n(x_i-\overline{x}{)}^2$ $s^2=\frac{1}{n-1}\sum _{i=1}^n(x_i-\overline{x}{)}^2$，后者为无偏方差，也是最常用的。（这是因为当${\sigma }^2$ 总体方差时，总有$E(s_{\ast }^2)=\frac{n-1}{n}{\sigma }^2$,$E(s^2)={\sigma }^2$，表明$s_{\ast }^2$ 系统偏小的误差，$s^2$ 此系统偏差。）称$\sqrt{s^2}$ 样本标准差。

     样本方差是样本的散布特征，$s^2$越大样本越分散，$s^2$ 小分布越集中，样本标准差比样本方差使用更频繁，因为前者和样本均值有着相同的单位。

   $s^2$ 计算有如下三个公式可供选用：

   $$s^2=\frac{1}{n-1}\sum (x_i-\overline{x}{)}^2=\frac{1}{n-1}[\sum x_i^2-\frac{(\sum x_i{)}^2}{n}]=\frac{1}{n-1}(\sum x_i^2-n{\overline{x}}^2)$$

   在分组样本场合，样本方差的近似计算公式为

   $$s^2=\frac{1}{n-1}\sum _{i=1}^k{f}_i(x_i-\overline{x}{)}^2=\frac{1}{n-1}(\sum _{i=1}^k{f}_i{x}_i^2-n{\overline{x}}^2)$$

   其中 k 为组数，$x_i,f_i$ 别为第 i 个区间的组中值与频数，$\overline{x}$ 分组样本的均值。

4. 样本矩及其函数

   • 样本的 k 阶原点矩$a_k=\frac{1}{n}\sum _{i=1}^n{x}_i^k$，样本均值$\overline{x}$ 样本的一阶原点矩；
   • 样本的 k 阶中心距$b_k=\frac{1}{n}\sum _{i=1}^n(x_i-\overline{x}{)}^k$，样本方差$s^2$ $s_{\ast }^2$ 为样本的二阶中心矩；
   • 样本变异系数$C_r=s/\overline{x}$；
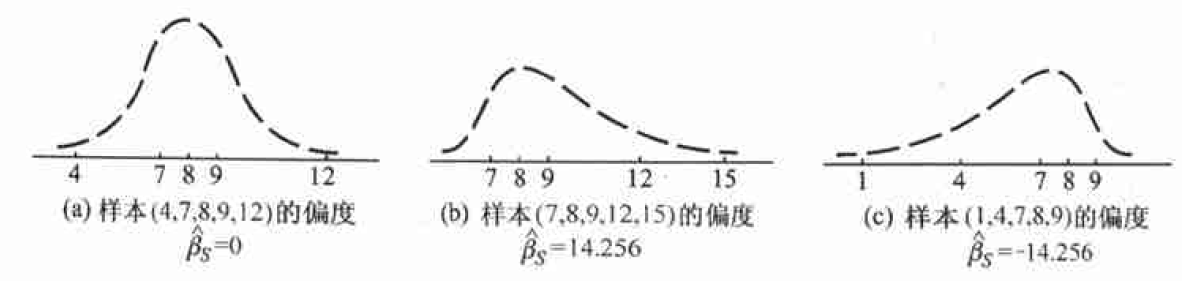
   • 样本的偏度$\widehat{{\beta }_s}=b_3/b_2^{3/2}$，反映样本数据与对称性偏离程度和偏离方向；
   • 样本的峰度$\widehat{{\beta }_k}=\frac{b_4}{b_2^2}-3$，反映总体分布密度曲线在其峰值附近的陡峭程度和尾部粗细.

5. 次序统计量及其分布

     设$x_1,...,x_n$ 取自某总体的一个样本，$x_{(i)}$ 为该样本的第 i 个次序统计量（升序排序后，第 i 个样本）。

   • $x_{(1)}=min\{x_1,...,x_n\}$ 为该样本的最小次序统计量；
   • $x_{(n)}=max\{x_1,...,x_n\}$ 为该样本的最大次序统计量；
   • $(x_{(1)},x_{(2)},...,x_{(n)}\}$ 为该样本的次序统计量，即不独立也不同分布；
   • $R=x_{(n)}-x_{(1)}$ 为样本极差。 设总体$X$ 密度函数为$f(x)$，分布函数为$F(x)$，$x_1,...,x_n$ 样本，则有
   • 样本第 k 个次序统计量$x_{(k)}$ 密度函数为
   $$f_k(x)=\frac{n!}{(k-1)!(n-k)!}(F(x){)}^{k-1}(1-F(x){)}^{n-k}f(x);$$
   • 样本第 i 个与第 j 个次序统计量的联合密度函数为
   $$f_{ij}(y,z)=\frac{n!}{(i-1)!(j-i-1)!(n-j)!}(F(y){)}^{i-1}(F(z)-F(y){)}^{j-i-1}(1-F(z){)}^{n-j}f(xy)f(z),y\le z,1\le i<j\le n$$

6. 样本中位数与样本分位数

   设$x_1,...,x_n$ 取自某总体的样本，$x_{(1)}\le x_{(2)}\le ...\le x_{(n)}$ 该样本的次序统计量，则样本中位数$m_{0.5}$ 义为

   $$m_{0.5}=\{\begin{array}{cc}{x}_{(\frac{n+1}{2})}& n\mathrm{为}\mathrm{奇}\mathrm{数}\\ \frac{1}{2}(x_{(\frac{n}{2})}+x_{(\frac{n}{2}+1)})& n\mathrm{为}\mathrm{偶}\mathrm{数}\end{array}$$

   样本的 p 分位数$m_p$ 义为

   $$m_p=\{\begin{array}{cc}{x}_{[np+1]}& np\mathrm{不}\mathrm{是}\mathrm{整}\mathrm{数}\\ \frac{1}{2}(x_{(np)}+x_{(np+1)})& np\mathrm{是}\mathrm{整}\mathrm{数}\end{array}$$

   其中[x]表示向下取整。中位数对样本的极端值有抗干扰性，或称有稳健性。 样本分位数的渐近分布：设总体的密度函数为$f(x)$，$x_p$ 总体的 p 分位数。若$p(x)$ $x_p$ 连续且$p(x_p)>0$，则当 n 充分大时，有

   $$\begin{gathered} m_p\sim N(x_p,\frac{p(1-p)}{n\cdot p^2(x_p)}), \\ {m}_{0.5}\sim N(x_{0.5},\frac{1}{4n\cdot p^2(x_{0.5})}) \end{gathered}$$

7. 五数概括与箱线图

     五数指用样本的五个次序统计量，即最小观测值，最大观测值，中位数，第一 4 分位数和第三 4 分位数。其图形为箱线图，可描述样本分布形状。