0. 摘要

持续学习（Continual Learning, CL）的目标是在非平稳的数据流中逐步学习不同的任务（如分类），而不遗忘旧任务。大多数 CL 工作专注于在从头学习的框架下应对灾难性遗忘。然而，随着基础模型的日益普及，配备了信息丰富表示的预训练模型已可用于各种下游需求。基于预训练模型的几种 CL 方法已经被探索，要么直接使用预提取的特征（这使得弥合分布差距具有挑战性），要么结合适配器（可能面临遗忘问题）。在本文中，我们提出了一种简洁而有效的方法，用于利用预训练模型进行 CL。鉴于遗忘发生在参数更新期间，我们考虑了一种替代方法，即利用无需训练随机投影器和类原型累积，从而绕过该问题。具体来说，我们在预训练模型的特征表示和输出头之间注入了一个带有非线性激活的冻结随机投影层，该层通过扩展维度捕捉特征之间的交互，为基于类原型的 CL 提供了增强的线性可分性。我们还展示了在使用预训练表示时，去相关类原型以减少分布差异的重要性。这些技术被证明是有效的，并且避免了在类和域增量持续学习中的遗忘问题。与应用于预训练 ViT-B/16 模型的先前方法相比，我们在七个类增量基准数据集上将最终错误率降低了 20% 到 62%，尽管没有使用任何回放记忆。我们得出结论，预训练模型在简单、有效和快速持续学习方面的潜力尚未被充分挖掘。代码可在 https://github.com/RanPAC/RanPAC 获取。

1. 引言

持续学习（Continual Learning, CL）是机器学习的一个子领域，在该领域中，模型必须从随时间变化的训练样本和/或监督信号分布中学习（通常分为一组不同的 T 个阶段/任务），同时在训练期间保持对先前学习内容的性能 [51,53]。传统的训练方法在 CL 中效果不佳，因为参数更新会偏向新样本，覆盖之前学到的内容。此外，在序列化且不相交的数据集上进行训练意味着没有机会学习不同阶段样本之间的差异 [48]。这些效应通常被称为“灾难性遗忘”[51]。

尽管已经提出了许多 CL 方法 [51,53,2,60]，但大多数方法专注于需要从头训练的模型，其性能在相同数据集上无法与非 CL 替代方案相媲美。尽管从头训练的有效用例始终存在，但大规模基础模型的新时代引发了将 CL 与强大的预训练模型优势相结合的日益增长的兴趣，即假设强大的通用特征提取器可以通过微调适应于任意数量的下游任务。

尽管在基于这种迁移学习的 CL 中仍然会发生遗忘 [57,65,63]（无论是使用传统的微调 [24] 还是更近期的参数高效迁移学习（Parameter-Efficient Transfer Learning, PETL）方法 [6,28,21]），但从强大的特征提取器开始进行 CL，为避免遗忘提供了新的思路，这些思路在从头训练时不太可能奏效。这些新方法已成功应用于预训练的 Transformer 网络 [39,10,57,56,46,20,65,63,47,55]、CNN[11,15,33,22,59,37] 和多模态视觉语言模型 [8]。

在这些提议中，明显存在三种主要策略（详见第 2 节）：(i) Transformer 网络的提示；(ii) 对预训练模型参数的谨慎选择性微调；(iii) 类原型（Class-Prototype, CP）累积。所有这些策略的共同点是不需要来自过去任务的回放样本缓冲区，这与从头训练模型的 CL 方法不同。相反，这些策略利用了预训练模型的强大特征提取能力。在相同的基准测试和预训练模型（例如 ViT B/16 Transformer 网络 [46,63,65]）下，每种策略在经验上都产生了可比的性能。因此，在性能、数据多样性和 CL 场景、简单性和效率方面，哪种策略最能利用预训练的基础模型仍是一个开放的问题。然而，我们注意到，基于 CP 的 CL 策略简单且适用于 CNN 和 Transformer 网络，而提示方法依赖于在 Transformer 网络输入前添加可学习的提示。微调预训练模型的参数比其他两种策略需要更多的训练资源，同时随着时间的推移累积遗忘的风险更大，因此需要额外的 CL 方法。

在本文中，我们展示了 CP 策略尚未充分发挥其准确性潜力，并且可以通过精心设计的策略来增强从预训练模型中提取的特征表示，从而实现突出的性能。基于 CP 的方法仅使用通过平均提取特征得到的原型来表示每个类，这在实际中存在与数据分布的差异。我们提出通过无需训练的冻结随机投影和去相关过程来处理这一问题，这两者都绕过了遗忘问题。具体来说，我们在预训练模型的特征层和基于 CP 的输出头之间引入了一个冻结的随机投影（Random-Projection, RP）层，该层具有非线性激活。

2. 相关工作

2.1 使用强大预训练模型的三种 CL 策略

Transformer 网络的提示：使用 ViT-B/16 网络 [9]，学习提示（Learning To Prompt, L2P）[57] 和 DualPrompt[56] 报告了相较于不利用预训练模型的最佳 CL 方法的显著改进，通过训练一小部分提示并在 CL 过程中更新。CODA-Prompt[46]、S-Prompt[55] 和 PromptFusion[5] 在此基础上进一步发展，展示了性能的改进。

对骨干网络的谨慎微调：SLCA[63] 发现，通过以比分类头更低的学习率微调 ViT 骨干网络，其准确性优于提示策略。然而，使用 softmax 时，需要引入“分类器对齐”方法，这会以每个类的特征协方差矩阵的形式带来高内存成本。另一个例子是选择性微调一些 ViT 注意力块 [47]，结合传统的 CL 方法 L2 参数正则化。微调也应用于 CLIP 视觉语言模型，结合成熟的 CL 方法 LwF[8]。

类原型（Class-Prototype, CP）累积：在 L2P 之后，有研究指出，对于 CL 图像分类器 [20]，通过在 ViT 模型的特征输出上附加最近类均值（Nearest Class Mean, NCM）分类器可以实现可比的性能（参见 [39]）。通过与仅在第一个 CL 阶段（“首次会话训练”）训练的 PETL 方法结合，可以显著提升这一策略 [65,37]。对于 Transformer 网络，[65] 考虑了三种 PETL 方法，而对于 CNN，[37] 使用了 FiLM 方法。与第一种策略（提示）类似，这些方法需要学习新参数，但避免更新骨干预训练网络的任何参数。重要的是，[37] 还展示了，通过累积嵌入特征的协方差矩阵并基于线性判别分析（LDA）[35] 学习线性分类头，简单的 NCM 分类器在准确性上很容易被超越。[37] 的简单且计算轻量的算法使得 CL 在首次会话之后可以完美地进行，完全避免了灾难性遗忘的可能性。

CP 通常非常适合 CL[42,7,31,16]，并且适用于预训练模型 [20,65,37]，因为当提取特征向量的模型被冻结时，跨 T 个任务累积的 CP 将相同，无论任务的顺序如何。此外，与使用回放缓冲区相比，其内存成本较低，回放缓冲区是许多 CL 方法 [53] 的组成部分。

2.2 用于创建特征交互的 RP 方法

如前所述，最初的非 CL 使用冻结 RP 层后接非线性投影的动机与我们不同，具有以下三个特性。首先，保持权重冻结消除了训练它们的计算成本。其次，当与线性输出层结合时，可以使用所有训练数据同时通过精确数值计算学习均方误差最优的输出权重（见附录 B.3），而不是迭代学习。第三，对随机投影的特征进行非线性激活的动机是假设特征之间的非线性随机交互可能比原始特征更具线性可分性。对非线性诱导的成对交互的特殊情况的分析可以在 [32] 中找到，并且对一般非线性（具有高阶交互）的数学性质也进行了广泛讨论，例如 [4,18]。

3. 背景

3.1 持续学习问题设置

我们假设通常的监督 CL 设置，即一系列 $T$ 个任务/阶段，$D=D_1,...,D_T$。在每个 Dt 中，提供了一组不相交的训练数据及其对应的标签以供学习。后续阶段无法访问旧数据。我们主要考虑“类增量学习”（Class-Incremental Learning, CIL）和“域增量学习”（Domain-Incremental learning, DIL）协议 [51] 用于图像分类。在 CIL 中，每个 Dt 的类标签是不相交的。CIL 的一个挑战性方面是，与任务增量学习（Task-Incremental Learning, TIL）相比，在 CIL 推理期间，任务身份以及每个样本的类子集是未知的 [51]。在 DIL 中，虽然所有阶段通常共享相同的类集，但每个阶段样本之间存在分布偏移。例如，D1 可能包含照片，而 D2 可能包含绘画图像。

我们引入 $K$ 作为 $T$ 个任务中考虑的总类数，每个任务中的训练样本数为 $N_t$，且 $N:=\sum _{t=1}^T{N}_t$。对于任务 $D_t$ 中的第 $n$ 个唯一训练样本，我们使用 $y_t,n$ 表示其长度为 $K$ 的 one-hot 编码标签，$f_{t,n}\in {\mathbb{R}}^L$ 表示从冻结的预训练模型中提取的特征。我们使用 ftest 表示测试实例的编码特征，我们希望为其预测标签。

3.2 使用预训练模型的类原型策略

对于 CL，使用传统的交叉熵损失通过线性探测或微调冻结预训练模型的特征表示会带来任务 - 新近偏差 [31] 和灾难性遗忘的风险。受益于预训练模型的高质量表示，最直接的类原型（Class-Prototype, CP）策略是使用最近类均值（Nearest Class Mean, NCM）分类器 [58,34]，如 [65,20] 所应用和研究的。每个类的 CP 通常通过平均类内训练样本的提取特征向量来构建，我们将类 $y$ 表示为 ${\overline{c}}_y$。在推理中，测试样本的类别通过找到其表示与 CP 集之间的最高相似性来确定。例如，[65] 使用余弦相似性来找到测试样本的预测类别，

$$\begin{array}{}\text{(1)}& y_{\text{test}}=\arg \underset{y^{\prime }\in \{1,\dots ,K\}}{max}{s}_{y^{\prime }},s_y:=\frac{f_{\text{test}}^{\mathrm{\top }}{\overline{c}}_y}{\parallel f_{\text{test}}\parallel \cdot \parallel {\overline{c}}_y\parallel }.\end{array}$$

然而，通过利用二阶特征统计量 [11,37]，在同一通用 CL 策略中超越 NCM 并不困难。例如，[37] 发现，使用预训练 CNN 的 CL 结果始终优于 NCM，使用增量版本的线性判别分析（LDA）分类 [35]，其中提取特征的协方差矩阵不断更新。在温和的假设下，LDA 等同于使用马氏距离（Mahalanobis distance）比较特征向量和类原型（见附录 B.4），即与 [65] 使用的余弦距离不同。

3.3 基于 Gram 矩阵逆的 CP 分类

我们还将使用增量计算的二阶特征统计量，但与 LDA 相比（见附录 B.4），我们通过使用特征的 Gram 矩阵 $G$ 和类原型 $c_y$（省略了平均操作）来简化计算，从而获得预测标签：

$$\begin{array}{}\text{(2)}& y_{\text{test}}=\arg \underset{y^{\prime }\in \{1,\dots ,K\}}{max}{s}_{y^{\prime }},s_y:=f_{\text{test}}^{\mathrm{\top }}{G}^{-1}{c}_y.\end{array}$$

与 LDA 类似，但与余弦相似性不同，这种形式利用训练集来“校准”相似性。该目标基于长期建立的用于预测 one-hot 编码类标签的最小二乘误差理论 [35]（见附录 B.3）。与增量 LDA[36,11] 类似，在 CL 训练期间，我们在第 4.3 节中描述了如何逐步更新 Gram 矩阵和对应于 $c_y$ 的 CP。需要注意的是，公式 (2) 以 $T$ 个任务后的最大类数 $K$ 表示。然而，对于 CIL，它可以在完成 $t<T$ 个任务后计算，此时类数小于 $K$。对于 DIL，通常在所有任务中都可以访问所有 $K$ 个类。

4. 提出的方法与理论见解：RanPAC

4.1 为什么二阶统计量对 CP 很重要

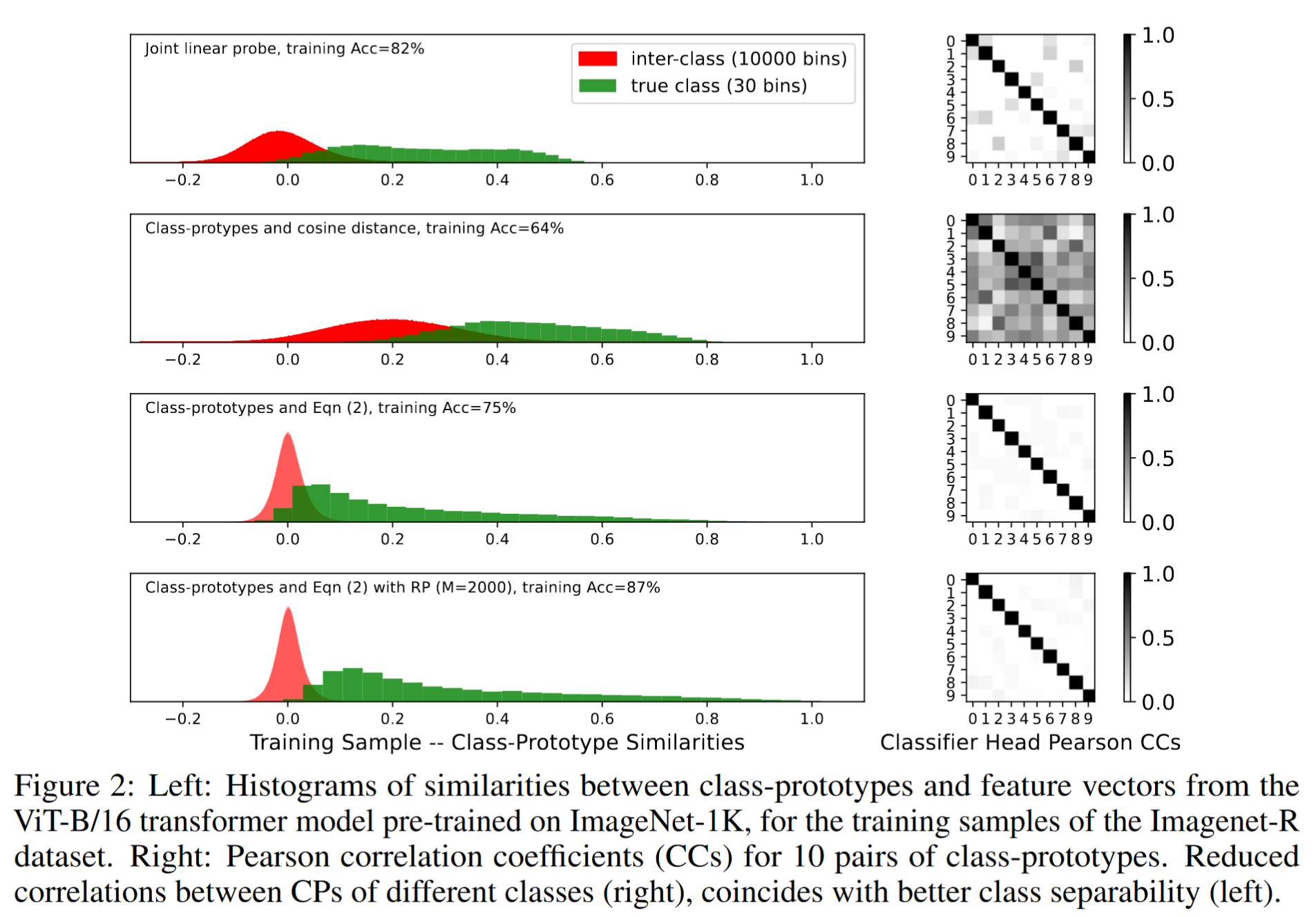
我们在第 5 节中展示了公式 (2) 比 NCM 带来更好的结果。我们将其归因于原始 CP 通常在类之间高度相关，导致余弦相似性校准不佳，而使用 LDA 或公式 (2) 主要消除了 CP 之间的相关性，从而在类之间创建了更好的可分性。为了说明这些见解，我们使用了一个在 ImageNet-21K 上预训练的 ViT-B/16 Transformer 模型 [9]，并移除了其分类头，数据来自成熟的 200 类 Split Imagenet-R CIL 基准 [56]。

为了与 CP 方法进行比较，我们在所有 200 类上联合训练了一个线性探测 softmax 分类器。我们将联合探测的权重视为类原型，然后计算每一对原型之间的 Pearson 相关系数，如图 2（右）所示的前 10 类。与线性探测相比，使用 NCM 时明显观察到非常高的非对角相关性，其均值是原始 ImageNet-1K 训练数据的两倍多。这说明了下游数据集的域偏移程度。然而，当使用公式 (2) 时，这些相关性大部分被消除。图 2（左）显示，高相关系数与类原型和训练样本之间的校准不佳的余弦相似性一致，无论是真实类比较（样本特征向量与其对应类标签的 CP 之间的相似性）还是类间比较（样本特征向量与不等于样本类标签的 N-1 个类的 CP 之间的相似性）。然而，当使用公式 (2) 时，结果（第三行）将训练集准确率从 64% 提高到 75%，同时减少了类间和真实类相似性分布的重叠，并显著降低了 CP 之间的非对角相关系数。最终结果是线性分类权重更接近联合训练的线性探测产生的权重。这些结果与公式 (2) 和去相关之间的已知数学关系一致，我们在附录 B.4.4 中概述了这些关系。

4.2 随机投影的详细概述与直觉

使用原始 ${\overline{c}}_y$ 的 CP 方法假设高斯分布具有3。经验上，我们发现当与预训练模型一起使用时，这一假设是无效的（图 2）。可以通过学习非线性函数（例如使用 SGD 训练神经网络）来缓解这一差距（例如，在第一个任务上学习适应 [65,37]），但这需要额外的假设和架构选择。此外，对于 CL，在所有任务上进行学习都会带来灾难性遗忘的高风险。相反，我们利用了 CP 策略中的目标主要需要首先进行特征投影（可能通过协方差矩阵调整其分布），其次需要特征原型的观察。对于后者，由于使用大型预训练模型生成的特征捕获了最显著的模式和属性，平均值是一个合理的类代表。然而，特征表示也可能受益于非线性变换以增强线性可分性。在本文中，我们考虑两点：(i) 我们展示了在嵌入空间（或将其投影到随机基）中对特征进行随机投影到更高维空间会导致更可能适合高斯拟合的分布（例如使用公式 (2)）；(ii) 当表示的分布接近高斯分布时，我们可以简单地执行线性回归（或 LDA 或联合高斯分布的条件均值）。

这一断言得到了图 2 底行的支持，该图显示，应用大小为 $M=2000$ 的 RP 层（为说明目的任意选择）进一步减少了相似性直方图之间的重叠，并将类内直方图向右移动，同时伴随更高的准确率，超过了联合线性探测的结果，这与我们在第 5 节中的发现一致。我们注意到，这些 RP 可以生成一次，然后在所有持续学习阶段冻结使用，从而实现简单且高效的算法。

我们首先分析从预训练模型中提取的特征在使用一些随机基向量（即随机投影）投影后的内积。我们考虑从方差为 ${\sigma }^2$ 的高斯分布中随机独立同分布（i.i.d.）抽取的 $M$ 个随机向量。数量 $M$ 定义了这些特征的随机投影所构成的空间维度。考虑随机投影 $W\in {\mathbb{R}}^{L\times M}$，对于任何两个给定的特征向量 $f,f^{\prime }\in {\mathbb{R}}^L$，我们有（见附录 B.2）：

$$\begin{array}{}\text{(3)}& {\mathbb{E}}_W[(W^{\mathrm{\top }}f{)}^{\mathrm{\top }}(W^{\mathrm{\top }}{f}^{\prime })]=\sum _i{\mathbb{E}}_W\left[W_{(i)}^2\right]f^{\mathrm{\top }}{f}^{\prime }+\sum _{i\ne j}{\mathbb{E}}_W\left[W_{(i)}^{\mathrm{\top }}\right]{\mathbb{E}}_W\left[W_{(j)}\right]f^{\mathrm{\top }}{f}^{\prime },\end{array}$$

其中 $W_{(i)}$ 表示第 $i$ 列。也就是说，这两个特征的投影的期望内积可以分解。现在，我们有 $W_{(i)}\sim \mathcal{N}(0,{\sigma }^{2}I)$，因此 ${\mathbb{E}}_W[W_{(i)}]={\mathbb{E}}_W[W_{(j)}]=0$，公式 (3) 中的第二项消失。此外，$\sum _i{\mathbb{E}}_W[W_{(i)}^2]=M{\sigma }^2$。我们可以得出两个观察结果（理论细节见附录 B.2）：

1. 随着 $M$ 的增加，任何投影特征的范数接近方差的可能性增加。换句话说，在高维空间中投影的向量几乎肯定位于分布的边界上，与均值的距离几乎相等（分布接近各向同性高斯分布）。
2. 随着 $M$ 的增加，两个随机投影实例之间的角度更可能是不同的（即投影空间中的内积更可能大于某个常数）。

这一讨论可以很容易地扩展到包含非线性。引入非线性的好处是：(i) 包含交互项 [54,50]；(ii) 模拟更高维的投影，否则可能在数量上过大。为了看到后一点，记 $\varphi$ 为感兴趣的非线性函数，我们有 $\varphi (W^{\mathrm{\top }}f)\approx {\hat{W}}^{\mathrm{\top }}\hat{f}$，其中 $\hat{f}$ 通过使用泰勒级数的线性扩展获得，$\hat{W}$ 是相应的投影。非线性函数 $\varphi$ 的泰勒级数展开引入了维度之间的高阶交互。尽管可以直接形成交互项的向量，如 [38,54] 的方法，但对于非平凡的 $L$，这在计算上是不可行的。因此，使用形式为 $h_{\text{test}}:=\varphi (f_{\text{test}}^{\mathrm{\top }}W)$ 的非线性投影是一种方便且计算成本低廉的替代方案，如在非 CL 环境中已知的有效工作 [43,4,18,32]。

4.3 用于持续学习的随机投影

使用上述随机投影，$\varphi (\cdot )$ 作为逐元素的非线性激活函数，给定特征样本 $f_{t,n}$，我们为每个任务中的 CL 训练获得长度为 $M$ 的表示，

$$h_{t,n}:=\varphi (f_{t,n}^{\mathrm{\top }}W)(\text{图 1})。$$

在推理中，$h_{\text{test}}:=\varphi (f_{\text{test}}^{\mathrm{\top }}W)$ 用于公式 (2) 中的 $s_y$ 代替 $f_{\text{test}}$。我们定义 $H$ 为 $M\times N$ 矩阵，其中列由所有 $h_{{}_{k,n}}$ 组成，为了方便起见，我们仅指在所有 $N$ 个样本使用后的最终 $H$。现在，我们有一个 $M\times M$ 的 Gram 矩阵 $G=H{H}^{\mathrm{\top }}$。上述讨论的随机投影仅采样一次，并在所有 CL 阶段中保持冻结。

与应用于 CL 的流式 LDA 中的协方差矩阵更新类似 [11,37]，变量可以逐个样本更新，或者一次更新整个 CL 阶段 $D_t$。我们引入矩阵 $C$ 来表示所有 $c_y$ 的列向量连接。与协方差 $S$ 不同，我们更新 Gram 矩阵和 $C$ 中的 CP（即 $c_y$ 的连接），这可以逐个任务或逐个样本完成，因为我们可以将 $G$ 和 $C$ 表示为外积的和：

$$\begin{array}{}\text{(4)}& G=\sum _{t=1}^T\sum _{n=1}^{N_t}{h}_{t,n}\otimes h_{t,n},C=\sum _{t=1}^T\sum _{n=1}^{N_t}{h}_{t,n}\otimes y_{t,n}.\end{array}$$

无论 $N$ 个训练样本的呈现顺序如何，$C$ 和 $G$ 都将保持不变，这是 CL 算法的理想属性。

公式 (2) 与最小二乘理论的起源具有实际用途；我们发现最好使用岭回归 [35]，并计算 $l_2$ 正则化逆 $(G+\lambda I{)}^{-1}$，其中 $I$ 表示单位矩阵。这是通过交叉验证系统地实现的，见附录 C。修订后的 CL 得分可以重写为：

$$\begin{array}{}\text{(5)}& s_y=\varphi (f_{\text{test}}^{\mathrm{\top }}W)(G+\lambda I{)}^{-1}{c}_y.\end{array}$$

在矩阵形式中，得分可以表示为对每个类标签的预测 $y_{\text{pred}}=h_{\text{test}}{W}_o$。与流式 LDA 不同，我们的方法具有以下优点：(i) 从得分中消除了偏差计算的需要；(ii) 更新 Gram 矩阵而不是协方差避免了均值的外积；(iii) 形式 $W_o=(G+\lambda I{)}^{-1}C$ 作为带有 $l_2$ 正则化的均方误差损失的闭式解出现（见附录 B.3），而在 NCM 中，没有这样的理论结果存在。算法 1 的第 2 阶段总结了上述 CL 计算。

公式 (5) 的应用表面上类似于 AdaptMLP 模块 [6]，但我们扩展到了维度 $M>L$，因为过去应用发现这对于补偿 $W$ 是随机的而不是学习的 [43,4,18,32] 是必要的。如引言所述，使用随机且无需训练的权重层特别适合 CL。

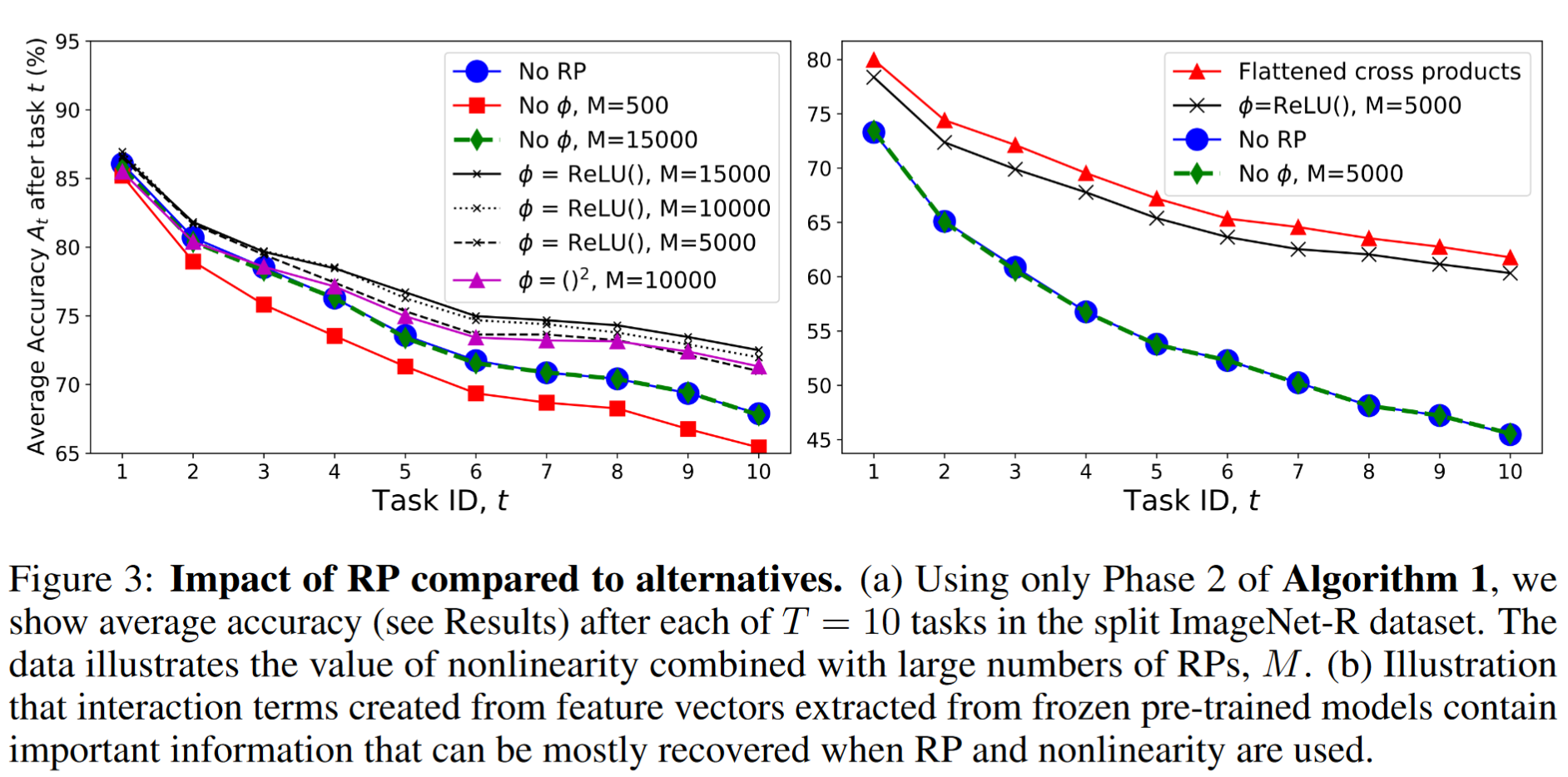
将原始特征转换为非线性随机投影的价值如图 3 所示。从预训练的 ViT-B/16[9] 网络中提取了 $T=10$ 个任务的 Split ImageNet-R CIL 数据集的特征，并在每个 $T=10$ 个任务后应用公式 (5)。图 3(a) 显示了典型的 CL 平均准确率趋势，即随着任务增加，准确率下降。当使用非线性激活 $\varphi (\cdot )$ 时（例如 ReLU 或平方），随着 $M$ 的增加，性能提高，但当省略非线性激活时，即使 $M$ 非常大，准确率也不比不使用 RP 更好。另一方面，如果维度在没有非线性的情况下减少（在这种情况下从 768 减少到 500），则性能低于不使用 RP 的情况，这表明如果 RP 在此应用中创建维度减少，会导致性能下降。

图 3(b) 说明了为什么非线性重要。我们仅使用每个样本的前 100 个提取特征，并比较公式 (2) 对原始特征向量（黑色）和成对交互项（蓝色轨迹）的应用。前者显著优于后者。然而，当使用公式 (5) 时（红色轨迹），与扁平化交叉积相比，性能下降相对较小。尽管这表明详尽创建特征乘积而不是 RP，但这在计算上是不可行的。作为替代方案，RP 是一种方便且计算成本低廉的方法，用于创建增强线性可分性的非线性特征交互，特别是在使用预训练模型的 CL 中具有特殊价值。

4.4 结合参数高效迁移学习和首次会话适应

使用 RP 层的好处是它是模型无关的，例如，它可以应用于任何特征提取器。我们展示它可以与 PETL 方法正交应用。PETL 对 CL 非常有吸引力，特别是那些不改变原始预训练模型学习参数的方法，例如 [10,28]。我们将 RP 与一种 PETL 方法结合，该方法使用与 CL 兼容的“首次会话”训练进行训练，如 [65,37] 所做的那样。这意味着仅在第一个 CL 任务 $D_1$ 上训练 PETL 参数，然后在此之后冻结它们（见算法 1 的第 1 阶段）。其理由是，第一个任务中的训练数据和标签可能比用于训练原始预训练模型的数据更具代表性。如果新数据集的漂移很大，例如在 DIL 中，由于这一选择，PETL 的好处可能会减少。但假设是预训练数据集和新数据集之间的域差距足够大，仍然会带来好处。

首次会话训练 PETL 参数需要一个临时线性输出层，使用 SGD 和交叉熵损失以及 softmax 进行训练，并且仅使用 $K_1$ 个类，该输出层在第 2 阶段之前被丢弃。对于 Transformer 网络，我们实验了与 [65] 相同的三种方法，即 AdaptFormer[6]、SSF[28] 和 VPT[21]。有关这些方法的详细信息，请参见引用的参考文献和附录 D。与 [65] 不同，我们不连接适应和未适应的特征，因为我们发现使用 RP 时，这几乎没有增加价值。

4.5 RP 层的内存使用

RP 层将类原型的总内存需求增加了 $1+(M-L)/L$ 倍，同时增加了 $LM$ 个冻结且不可训练的参数。对于典型的 $L=768$ 和 $K=200$，注入大小为 $M=10000$ 的 RP 层因此创建了约 10 倍的可训练参数数量，并增加了约 10M 的不可训练参数。尽管这是一个显著的新参数数量，但与 ViT-B/16 模型的 8400 万参数总数相比，它仍然很小。此外，$W$ 的权重可以是双极的，如果每个元素使用单个比特存储，则对额外模型内存的贡献极小。在训练期间，我们还需要更新一个 $M\times M$ 的 Gram 矩阵，如果 $M<\sqrt{KL}$，则它比 SLCA 微调方法 [63] 的 $K(L\times L)$ 协方差矩阵更小。L2P[57]、DualPrompt[56] 和 ADaM[65] 各自使用约 0.3M–0.5M 的可训练参数。对于 $K=200$ 个类和 $M=10000$，RanPAC 使用更多的参数（约 2–2.5M，取决于 PETL 方法），与 CODA-Prompt[46] 相当。RanPAC 还使用了 10M 未训练参数，但我们强调这些参数是不可训练的。此外，$M$ 不必高达 10000（表 A5）。

5. 实验

我们将算法 1 应用于 CIL 和 DIL 基准测试。对于预训练模型，我们主要实验了两个 ViT-B/16 模型 [9]，如 [65] 所述：一个在 ImageNet-21K 上进行自监督训练，另一个在 ImageNet-1K 上进行有监督微调。比较使用标准的 CL 指标，平均准确率 [30]，定义为 $A_t=\frac{1}{t}\sum _{i=1}^t{R}_{t,i}$，其中 $R_{t,i}$ 是在第 $t$ 个任务训练后对第 $i$ 个任务的分类准确率。我们在主论文中报告最终准确率 $A_T$，并将每个 $A_t$ 和 $R_{t,i}$ 的分析留给附录 F，同时还包括遗忘指标和跨种子变异性的分析。附录 F 还显示，我们的方法在 ResNet 和 CLIP 骨架上表现良好。

我们使用了以前用于 CIL 或 DIL 的分割数据集（见表 1 和表 3 中的引用）；详细信息见附录 E。我们在算法 1 中使用 $M=10000$，除非另有说明；对 $M$ 的扩展研究见附录 F.5。所有列出的“联合”结果都是对 $D$ 的全部数据进行非 CL 训练的比较，使用交叉熵损失和 softmax。

CIL 的关键指示性结果如表 1 所示，对于 $T=10$，阶段大小相等（除了 VTAB，它是 $T=5$，与 [65] 相同）。对于 $T=5$ 和 $T=20$，见附录 F。对于每个数据集，我们的最佳方法以较大的优势超过了提示方法和 [20] 和 [65] 的 CP 方法的准确率。表 1 中列出的算法 1 的消融实验表明，当使用 PETL 时，包含我们的 RP 层可将错误率降低 11% 到 28%。如果不使用 PETL，增益会减少，但除了 VTAB 外，增益仍≥8%。表 1 还突出了 NCM 的局限性。

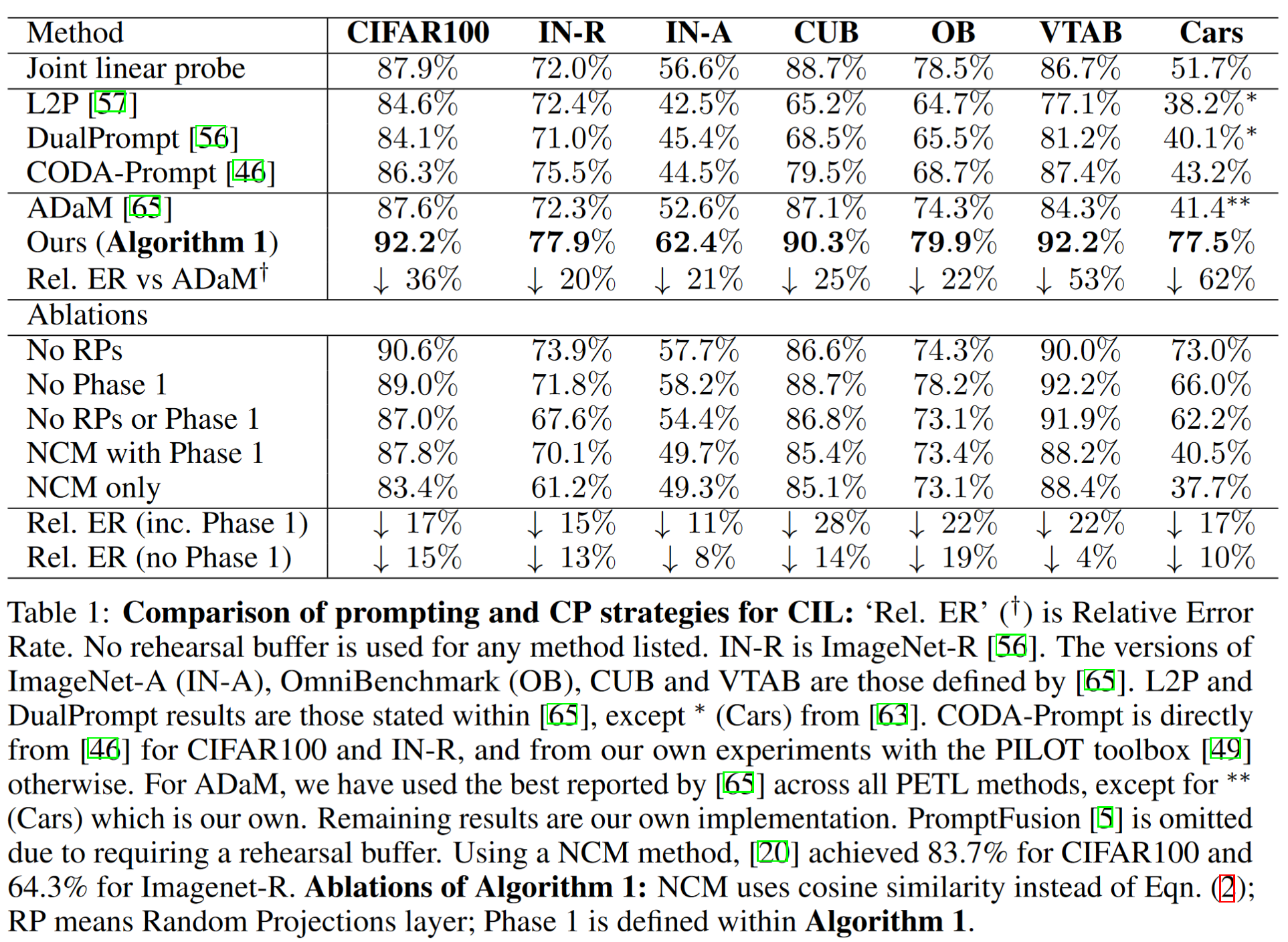
表 2 显示，算法 1 在 CIL 上的表现也优于微调策略 [47,63]。这与表 1 分开列出，因为微调有主要缺点，如引言中所述。表 2 还显示，算法 1 在三个数据集上接近最佳联合微调准确率的 2% 以内，而在两个 ImageNet 变体和 Cars 数据上差距较大。

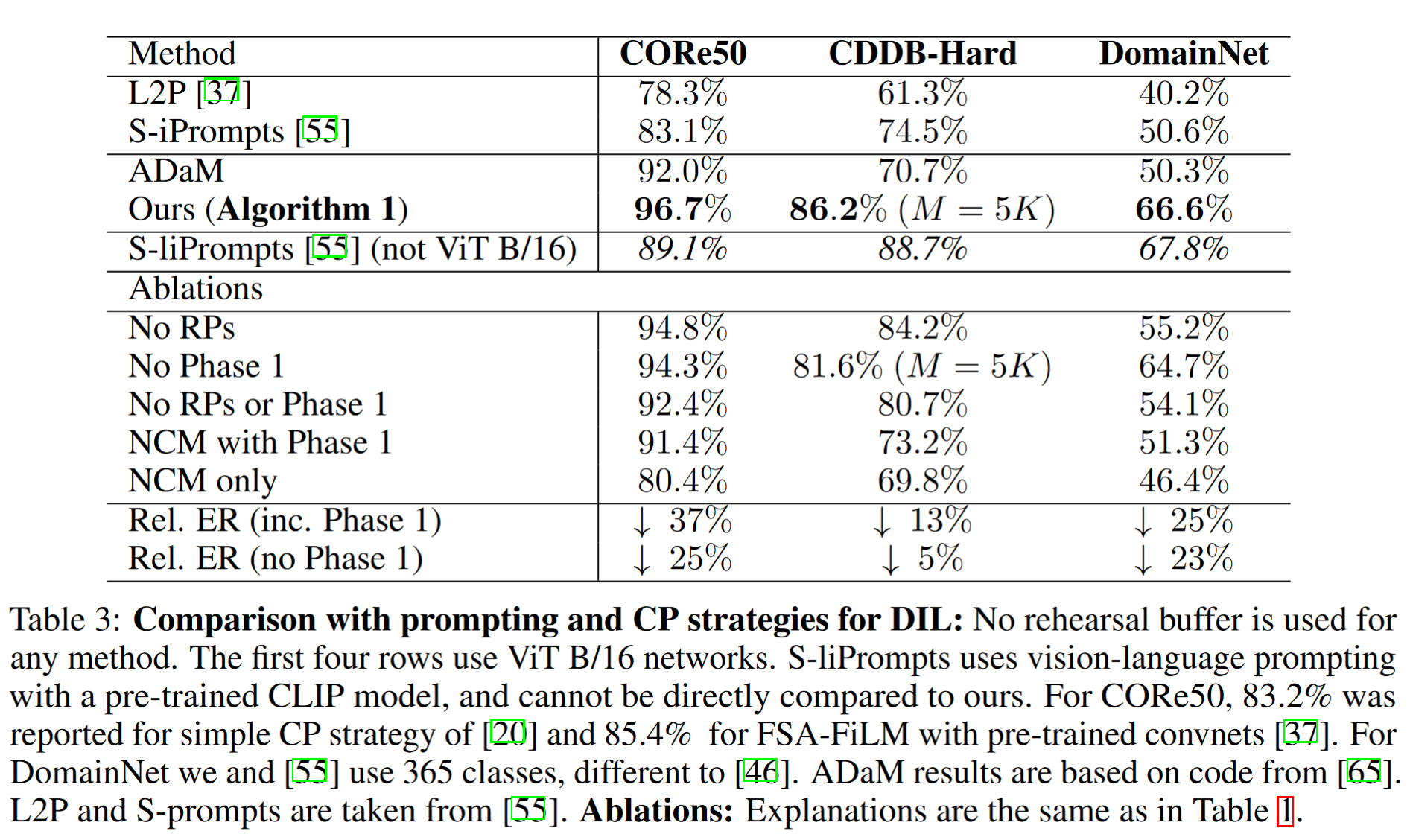
DIL 数据集的结果以及算法 1 的相应消融实验列在表 3 中。CORe50 是 $T=8$ 个阶段，50 个类 [29]，CDDB-Hard 是 $T=5$，2 个类 [27]，DomainNet 是 $T=6$，345 个类 [40]（更多详细信息见附录 E）。可以观察到与 CIL 相同的趋势，即比提示策略更好的性能，并突出了 RP 层的价值。对于 DomainNet，RP 的价值特别强，而包含 PETL 几乎没有增加价值，这与 DIL 的性质一致，其中不同的 CL 阶段来自不同的域。

6. 结论

我们已经证明，从预训练的基础模型（如 ViT-B/16）中提取的特征表示在持续学习中的潜力尚未被充分挖掘。应用我们简单且无需回放的类原型策略 RanPAC，可以在多样的 CL 基准数据集上显著降低错误率，同时避免了预训练模型中的遗忘问题。这些发现突显了在预训练模型中使用 CP 策略的益处。

局限性：公式 (4) 和 (5) 的价值完全依赖于提供良好的通用特征提取器。因此，如果用于从零开始训练网络的 CL 方法，它们不太可能同样强大。然而，现有的利用自监督学习或其他方式创建良好特征提取器骨干的 CL 方法可能会利用类似我们的方法进行下游 CL 任务。如第 4.5 节所述，RanPAC 使用比 L2P 等方法更多的参数。然而，这种权衡值得，因为实现简单且训练成本低。

未来工作：附录 F 中的示例表明，我们的方法在其他 CL 协议中也表现良好，包括：(i) 任务不可知的 CL，即训练期间没有任务边界（例如高斯调度的 CIFAR-100），(ii) 使用非 one-hot 编码目标，例如 CLIP 模型中的语言嵌入，(iii) 回归目标，这需要将类原型的概念扩展到通用特征原型。每种情况都有很大的扩展和探索空间。其他有趣的实验，我们留给未来工作，包括将我们的方法与提示方法结合的研究，以及（特别是对于 DIL）研究是否可以在不引起灾难性遗忘的情况下在首次会话之后训练 PETL 参数。预训练模型的少样本学习 [1,45] 也可能从类似 RanPAC 的算法中受益。

附录 A RanPAC 概述及与其他策略的比较

图 A1 提供了算法 1 中两个阶段的图形概述。表 A1 总结了利用预训练模型进行持续学习（CL）的不同策略，并比较了我们自己的方法 RanPAC。

图 A1：RanPAC 的 CL 分类概述。在算法 1 的第 1 阶段，我们可选地将参数高效迁移学习（PETL）方法的参数注入到冻结的预训练模型（PTM）中。PETL 参数仅在任务 1（“首次会话”）上进行训练，以帮助弥合域差距，如 [65,37] 所示。然后在第 2 阶段，首先从网络提取 $L$ 维特征向量 $f$，然后使用冻结的权重 $W$ 将提取的特征向量随机投影到维度 $M$（通常 $M>L$），并通过非线性激活 $\varphi$ 获得新的特征向量 $h=\varphi (f^{\mathrm{\top }}W)$。第 2 阶段的训练包括不断迭代更新类原型和 Gram 矩阵，然后在每个任务训练结束后通过矩阵逆计算 $M\times N$ 矩阵 $W_o$。这些权重可以被视为去相关的类原型，用于线性加权特征 $h$ 以获得类预测 $y$。

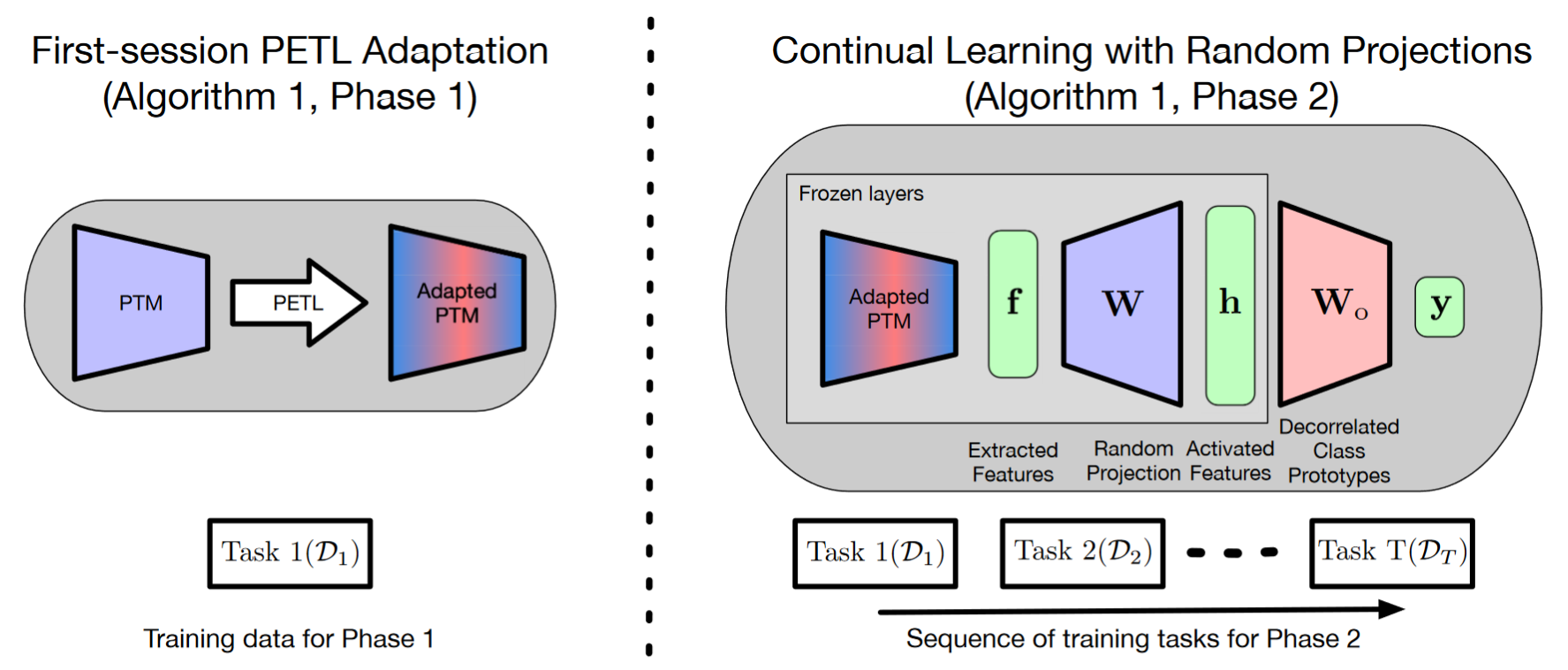
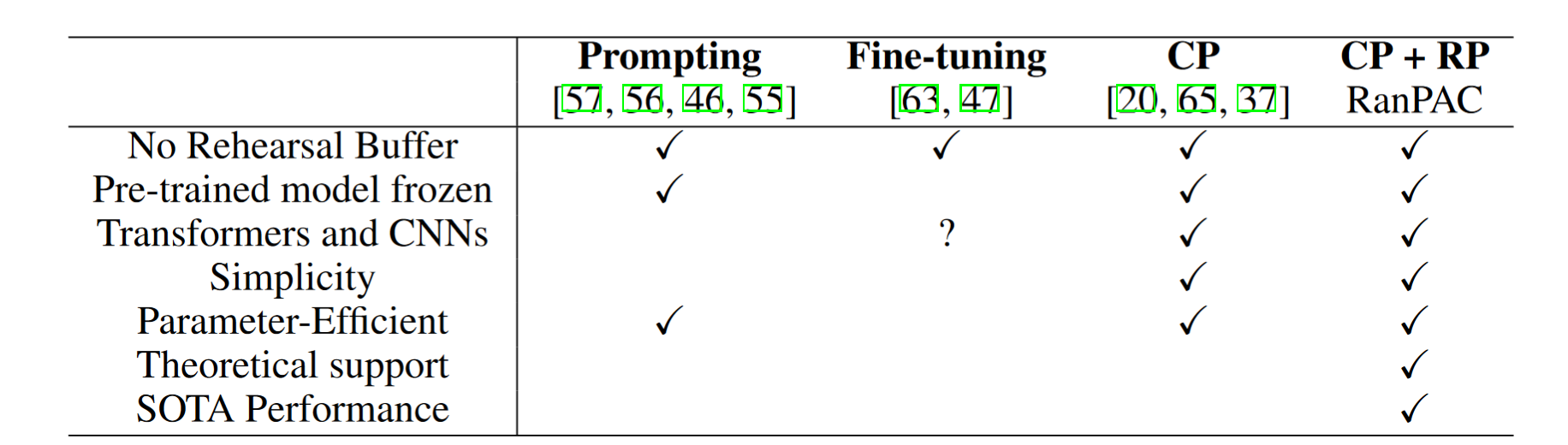
表 A1：不同策略的比较。在第 1 节中，我们将利用预训练模型进行 CL 的现有方法分为三种策略：提示、微调和类原型（CP）。我们自己的方法 RanPAC 是一种 CP 策略，其中我们引入了带有非线性激活的冻结随机投影（RP）层。总体而言，我们认为 CP 方法提供了最佳的组合优势，而在现有的 CP 方法中，RanPAC 提供了最强的结果，并得到了其使用 RP 和二阶统计量去相关 CP 的理论支持。我们注意到，回放缓冲区已被用于一些引用的方法以提高性能，并且可能也可以用于尚未使用它们的方法，例如 RanPAC。

附录 B 理论支持

B.1 投影向量范数的 Chernoff 界

我们提供了第 4.2 节讨论的进一步细节。使用 Chernoff 界，投影向量的范数可以写为：

$$\begin{array}{}\text{(6)}& P(|\parallel W^{\mathrm{\top }}f\parallel -{\mathbb{E}}_W[\parallel W^{\mathrm{\top }}f\parallel ]|>\epsilon {\sigma }^2)\le 2\exp (-\frac{{\epsilon }^2{\sigma }^2}{2M+\epsilon }).\end{array}$$

这个界表明了维度与投影向量范数的期望变化之间的关系。对于固定的 $\sigma$ 和 $\epsilon$，随着 $M$ 的增加，右侧趋近于 1，表明投影向量的范数更可能处于与期望的期望距离内。换句话说，这些投影向量在高维空间几乎肯定位于分布的边界上，与均值的距离几乎相等（分布接近各向同性高斯分布）。

B.2 增加投影维度的影响

投影向量的 Gram 矩阵可以通过考虑任意两个向量 $f,f^{\prime }$ 的内积获得。如公式 (3) 所示，这可以推导为：

$$\begin{array}{}\text{(7)}& {\mathbb{E}}_W[(W^{\mathrm{\top }}f{)}^{\mathrm{\top }}(W^{\mathrm{\top }}{f}^{\prime })]={\mathbb{E}}_W[(f^{\mathrm{\top }}W)(W^{\mathrm{\top }}{f}^{\prime })]={\mathbb{E}}_W[\sum _i{W}_{(i)}^2{f}^{\mathrm{\top }}{f}^{\prime }+\sum _{i\ne j}{W}_{(i)}^{\mathrm{\top }}{W}_{(j)}{f}^{\mathrm{\top }}{f}^{\prime }]=\sum _i{\mathbb{E}}_W\left[W_{(i)}^2\right]f^{\mathrm{\top }}{f}^{\prime }+\sum _{i\ne j}{\mathbb{E}}_W\left[W_{(i)}^{\mathrm{\top }}\right]{\mathbb{E}}_W\left[W_{(j)}\right]f^{\mathrm{\top }}{f}^{\prime },\end{array}$$

其中第二项对于任何两个零均值独立抽取的随机向量 $W_{(i)},W_{(j)}$ 为零。我们可以从这个扩展中得出以下结论：

1. 使用 Chernoff 不等式，对于任意两个向量，我们有：

$$\begin{array}{}\text{(8)}& P(|(W^{\mathrm{\top }}f{)}^{\mathrm{\top }}(W^{\mathrm{\top }}{f}^{\prime })-{\mathbb{E}}_W[(W^{\mathrm{\top }}f{)}^{\mathrm{\top }}(W^{\mathrm{\top }}{f}^{\prime })]|>{\epsilon }^{\prime }M{\sigma }^2)\le 2\exp (-\frac{{\epsilon }^{\prime 2}M{\sigma }^2}{2+{\epsilon }^{\prime }}).\end{array}$$

这个界表明，随着投影维度的增加，任意两个向量及其投影的内积更可能是不同的。换句话说，随着 $M$ 的增加，两个向量及其投影的内积相等的可能性越来越小。

2. 随着 $M$ 的增加，任意两个随机投影实例的内积更可能是不同的（即投影空间中的内积更可能大于某个常数）。这是因为，使用马尔可夫不等式，对于更大的 $M$，更容易选择更大的 ${\epsilon }^2$ 满足：

$$\begin{array}{}\text{(9)}& P(|(W^{\mathrm{\top }}f{)}^{\mathrm{\top }}(W^{\mathrm{\top }}{f}^{\prime })|\ge {\epsilon }^2)\le \frac{M{\sigma }^2}{{\epsilon }^2}.\end{array}$$

B.3 与最小二乘法的联系

公式 (5) 的得分可以写成矩阵形式：

$$\begin{array}{}\text{(10)}& y_{\text{test}}=h_{\text{test}}(G+\lambda I{)}^{-1}C,\end{array}$$

其中 $h_{\text{test}}:=\varphi (f_{\text{test}}^{\mathrm{\top }}W)$ 是经过逐元素非线性激活 $\varphi (\cdot )$ 后的随机投影激活。形式 $W_o:=(G+\lambda I{)}^{-1}C$ 源于最小二乘回归的基本理论。我们可以将其写为：

$$\begin{array}{}\text{(11)}& W_o=(G+\lambda I{)}^{-1}H{Y}_{\text{train}},\end{array}$$

其中 $Y_{\text{train}}$ 是一个 $N\times K$ 的 one-hot 编码目标矩阵，$H$ 如第 4.3 节定义。公式 (12) 是 $l_2$ 正则化方程组的最小均方误差解，定义为：

$$\begin{array}{}\text{(12)}& Y_{\text{train}}^{\mathrm{\top }}=W_o^{\mathrm{\top }}H.\end{array}$$

对于参数 $\lambda \ge 0$，这通常表示为：

$$\begin{array}{}\text{(13)}& W_o={\text{argmin}}_W(\parallel Y_{\text{train}}^{\mathrm{\top }}-W^{\mathrm{\top }}H{\parallel }_2^2+\lambda \parallel W{\parallel }_2^2).\end{array}$$

因此，在不使用 CL 时，使用均方误差损失和权重衰减等于 $\lambda$ 来优化线性输出头将产生一个损失下界，该下界由直接计算 $W_o$ 实现。

B.4 与线性判别分析、马氏距离和 ZCA 白化的联系

我们使用公式 (2) 而不是 LDA 的原因有两个。首先，我们的公式是均方误差最优的，如 B.3 节所述。其次，使用逆 Gram 矩阵比使用协方差矩阵带来了两个便利的简化：(i) 公式 (2) 的简单形式可以用于推理，而不需要从类原型计算的偏差；(ii) 在 CL 过程中累积 Gram 矩阵和类原型的更新，如公式 (4) 所示，比使用协方差矩阵更高效。

我们现在通过理论推导得出这些结论。这些推导表明，使用公式 (2) 等同于在训练集的特征向量上应用带有 $l_2$ 正则化的均方误差损失函数来学习线性分类器。这些推导适用于 CL 和非 CL 情境。对于 CL，关键是要认识到，无论数据以何种序列到达进行训练，CP 和二阶统计量都可以以相同的方式累积。

B.4.1 预备知识：类原型

在任务 $T$ 后的 CL 类原型可以定义为：

$$\begin{array}{}\text{(14)}& {\overline{c}}_y=\frac{1}{n_y}\sum _{t=1}^T\sum _{n=1}^{N_t}{h}_{t,n}{I}_{t,n},y=1,\dots ,K,\end{array}$$

其中 $I_{t,n}$ 是一个指示函数，如果第 $t$ 个任务中的第 $n$ 个训练样本属于类 $y$，则值为 1，否则为 0，$n_y$ 是每个类中的训练样本数，$h_{t,n}$ 是一个 $M$ 维的投影和激活特征向量。对于 RanPAC，我们省略均值并使用：

$$\begin{array}{}\text{(15)}& c_y=\sum _{t=1}^T\sum _{n=1}^{N_t}{h}_{t,n}{I}_{t,n},y=1,\dots ,K.\end{array}$$

对于最近类均值（NCM）分类器，以及 [65] 使用的余弦相似性度量，分类得分为：

$$\begin{array}{}\text{(16)}& s_y=\frac{f_{\text{test}}^{\mathrm{\top }}{\overline{c}}_y}{\parallel f_{\text{test}}\parallel \cdot \parallel {\overline{c}}_y\parallel },y=1,\dots ,K,\end{array}$$

其中 ${\overline{c}}_y$ 是从特征向量 $f_{t,n}$ 而不是 $h_{t,n}$ 计算的。这些余弦相似性仅依赖于一阶特征统计量，即每个类的平均特征向量。相比之下，LDA 和我们的方法使用二阶统计量，即特征向量内特征之间的相关性。

B.4.2 与 LDA 和马氏距离的关系

公式 (2) 的形式类似于线性判别分析（LDA）分类 [35]。对于 LDA，选择 $f_{\text{test}}$ 的预测类别的得分通常表示为权重和偏差形式：

$$\begin{array}{}\text{(17)}& {\psi }_y=f_{\text{test}}a+b\end{array}$$$$\begin{array}{}\text{(18)}& =f_{\text{test}}^{\mathrm{\top }}{S}^{-1}{\overline{c}}_y-0.5{\overline{c}}_y^{\mathrm{\top }}{S}^{-1}{\overline{c}}_y+\log ({\pi }_y),y=1,\dots ,K,\end{array}$$

其中 $S$ 是 $M$ 维特征向量的协方差矩阵，${\pi }_y$ 是类 $y$ 的频率。

找到最大的 ${\psi }_y$ 等同于最小化涉及马氏距离 $d_M:=\sqrt{(f_{\text{test}}-{\overline{c}}_y{)}^{\mathrm{\top }}{S}^{-1}(f_{\text{test}}-{\overline{c}}_y)}$ 的表达式，即最小化：

$$\begin{array}{}\text{(19)}& {\hat{\psi }}_y=d_M^2-\log ({\pi }_y^2)\end{array}$$$$\begin{array}{}\text{(20)}& =(f_{\text{test}}-{\overline{c}}_y{)}^{\mathrm{\top }}{S}^{-1}(f_{\text{test}}-{\overline{c}}_y)-\log ({\pi }_y^2),y=1,\dots ,K.\end{array}$$

这种形式表明，如果所有类别的概率相等，则最小化马氏距离足以进行 LDA 分类。

B.4.3 与 ZCA 白化的关系

我们现在考虑 ZCA 白化 [23]。该过程使用马氏变换 $D_Z=S^{-0.5}$ 线性变换数据 $H$ 为 $D_{Z}H$。将 $S$ 代入公式 (20) 得到：

$$\begin{array}{}\text{(21)}& {\hat{\psi }}_y=(D_Z(f_{\text{test}}-{\overline{c}}_y){)}^{\mathrm{\top }}(D_Z(f_{\text{test}}-{\overline{c}}_y))-\log ({\pi }_y^2)\end{array}$$$$\begin{array}{}\text{(22)}& =\parallel D_Z(f_{\text{test}}-{\overline{c}}_y){\parallel }_2^2-\log ({\pi }_y^2),y=1,\dots ,K.\end{array}$$

这种形式表明，如果所有类别的概率相等，则 LDA 分类等同于在 ZCA 白化后最小化欧几里得距离。

B.4.4 去相关类原型

公式 (2) 的得分可以通过强调与马氏变换的相似性和差异性的方式推导。这里我们使用随机投影特征 $h$ 而不是提取特征 $f$。我们选择一个线性变换矩阵 $D\in {\mathbb{R}}^{M\times M}$，将 Gram 矩阵 $G=H{H}^{\mathrm{\top }}$ 转换为单位矩阵，即 $D$ 必须满足：

$$\begin{array}{}\text{(23)}& (DH)(DH{)}^{\mathrm{\top }}=I_{M\times M}.\end{array}$$

很容易看出 $D^{\mathrm{\top }}D=(H{H}^{\mathrm{\top }}{)}^{-1}=G^{-1}$。接下来，将测试样本和类原型视为与 $H$ 来自相同分布，我们可以考虑点积：

$$\begin{array}{}\text{(24)}& {\hat{s}}_y=(D{h}_{\text{test}}{)}^{\mathrm{\top }}(D{c}_y)=h_{\text{test}}^{\mathrm{\top }}{G}^{-1}{c}_y,y=1,\dots ,K.\end{array}$$

因此，与公式 (14) 的最小均方误差公式得出的相似性相同。与马氏变换 $D_Z=S^{-0.5}$ 相比，这里的区别在于 Gram 矩阵等于单位矩阵而不是协方差矩阵。

LDA 与我们的方法相同，如果所有类别的概率相等且 $G=S$，这通常发生在所有 $M$ 特征的均值为零时，但这在一般情况下并不成立。

附录 C 训练与实现

C.1 在算法 1 中优化岭回归参数

参考算法 1 的最后一步，我们按如下方式优化 $\lambda$。对于第 2 阶段中的每个任务 $t$，该任务的训练数据被随机分为 80:20 的比例。我们对 $\lambda$ 进行了 17 个数量级的参数扫描，即 $\lambda \in \{{10}^{-8},{10}^{-7},\dots ,{10}^8\}$，对于每个 $\lambda$ 值，使用仅前 80% 的训练数据更新 $C$ 和 $G$，然后计算 $W_o=(G+\lambda I{)}^{-1}C$。我们随后计算剩余 20% 训练数据的预测 $h^{\mathrm{\top }}{W}_o$ 与目标之间的均方误差。然后选择在此 20% 分割上最小化均方误差的 $\lambda$ 值。因此，$\lambda$ 在每个任务后更新，并以与 CL 兼容的方式计算，即不访问先前训练任务的数据。值得注意的是，优化 (\lambda) 到一个数量级之间的值可能会略微提高准确率。此外，仅为当前任务的数据选择 (\lambda) 可能相对于在相同数据上进行非 CL 学习不是最优的，在这种情况下，明显的区别是优化 (\lambda) 在整个训练集的子集上。

C.2 训练细节

对于算法 1 的第 2 阶段，训练数据的使用如下。对于每个样本，从冻结的预训练模型中提取特征，以更新 (G) 和 (C) 矩阵。然后我们使用矩阵逆和乘法计算 (W_o)。因此，在第 2 阶段不需要基于 SGD 的权重更新。

对于算法 1 的第 1 阶段，我们使用 SGD 训练 PETL 方法的参数，即 AdaptFormer[6]、SSF[28]和 VPT[21]。对于每种方法，我们使用批量大小为 48，学习率为 0.01，权重衰减为 0.0005，动量为 0.9，并使用余弦退火调度，最终学习率为 0。通常我们训练 20 个 epoch，但如果在某些实验中明显过拟合，则减少到更少的 epoch。当使用这些方法时，使用 softmax 和交叉熵损失。类的数量等于第一个任务中的类数，即 (N_1)。生成的训练权重和头在第 2 阶段开始之前被丢弃。

对于表 1 中使用线性探测报告的数据，我们使用批量大小为 128，分类头中的学习率为 0.01，权重衰减为 0.0005，动量为 0.9，并训练 30 个 epoch。对于完全微调（表 2），我们使用相同的设置，但在主体（ViT 骨干的预训练权重）中使用学习率 0.0001。我们使用固定的学习率调度，没有减少学习率。我们发现对于微调，主体中的学习率低于头部对于最佳性能至关重要。

所有数据集的训练数据增强包括随机调整大小然后裁剪到 224×224 像素，以及随机水平翻转。对于推理，图像调整大小为短边 256，然后中心裁剪到 224×224，除了 CIFAR100，它只是从原始 32×32 调整到 224×224。

鉴于我们主要与[65]的结果进行比较，我们在主要实验中使用相同的种子，即种子值为 1993。这使得我们能够在消融中获得与[65]相同的结果。然而，我们注意到我们使用平均准确率作为主要指标，而[65]在其公共存储库中计算每个任务后的总体准确率，这可能与平均准确率略有不同。对于第 F 节中的变异性研究，我们还使用种子 1994 和 1995。

C.3 训练和推理速度

使用 RanPAC 进行推理的速度与原始预训练网络的速度几乎没有差异，因为 RP 层和输出线性分类头（由去相关类原型组成）都作为简单全连接层实现。对于训练，第 1 阶段使用 SGD 训练 PETL 参数 20 个 epoch，在训练集的 ((1/T)) 上进行，因此比联合训练快得多。第 2 阶段通常仅比以推理模式运行所有训练数据稍慢，因为骨干网络被冻结。最慢的部分是 Gram 矩阵的逆，在 (\lambda) 选择期间，但对于 (M = 10000)，这在 CPU 上大约为每个任务 1 分钟，如果需要可以进一步优化。我们认为，与替代方案相比，我们方法的效率和简单性非常强。

C.4 计算

所有实验均在运行 Ubuntu 22.04.2 LTS 的单台 PC 上进行，具有 32 GB RAM 和 Intel Core i9-13900KF x32 处理器。加速由单个 NVIDIA GeForce 4090 GPU 提供。

附录 D 参数高效迁移学习（PETL）方法

我们实验了与[65]相同的三种方法，即 AdaptFormer[6]、SSF[28]和 VPT[21]。详细信息见[65]。对于 VPT，我们使用深度版本，提示长度为 5。对于 AdaptFormer，我们使用与[65]相同的设置，即投影维度为 64。

附录 E 数据集

E.1 类增量学习（CIL）数据集

我们使用的七个 CIL 数据集总结在表 A2 中。对于 ImageNet-A、CUB、OmniBenchmark 和 VTAB，我们使用了[65]定义和详细说明的特定训练-验证分割。这四个数据集以及由[56]创建的 ImageNet-R 从 https://github.com/zhoudw-zdw/RevisitingCIL 提供的链接下载。CIFAR100 通过 torchvision 访问。Stanford Cars 从 https://ai.stanford.edu/~jkrause/cars/car_dataset.html 下载。

对于 Stanford Cars 和 (T = 10)，我们使用 (t = 1) 中的 16 个类和后续 9 个任务中的 20 个类。有趣的是，VTAB 具有 CIL 和 DIL 的特征。与我们使用的三个 DIL 数据集不同，VTAB 在每个任务中引入了不同域中的不相交集类。因此，我们仅对 VTAB 使用 (T = 5)，而对其他 CIL 数据集探索 (T = 5)、(T = 10) 和 (T = 20)。

表 A2：CIL 数据集。我们列出了每个数据集的原始来源和分割 CL 版本的参考文献。在列标题中，(N) 是训练样本总数，(K) 是所有任务训练后的类数，# val 样本是标准验证集中的验证样本数。

E.2 域增量学习（DIL）数据集

对于 DIL，我们在表 A3 中列出了每个数据集的域。更多详细信息见表 A3 第一列中引用的参考文献。与之前的工作一样，验证数据包括来自每个域的样本，但对于 CDDB-Hard 和 DomainNet，三个完整域保留用于 CORe50。

附录 F 附加结果

F.1 预备知识

我们提供了以平均准确率和平均遗忘度衡量的结果。平均准确率定义为[30]：

$$\begin{array}{}\text{(25)}& A_t=\frac{1}{t}\sum _{i=1}^t{R}_{t,i},\end{array}$$

其中 (R_{t,i}) 是在第 (t) 个任务训练后对第 (i) 个任务的分类准确率。平均遗忘度定义为[3]：

$$\begin{array}{}\text{(26)}& F_t=\frac{1}{t-1}\sum _{i=1}^{t-1}\underset{t^{\prime }\in \{1,2,\dots ,t-1\}}{max}(R_{t^{\prime },i}-R_{t,i}).\end{array}$$

对于 CIL，我们计算 (R_{t,i}) 为 (D_i) 中类子集的准确率。对于 DIL，由于所有类都存在于每个任务中，(R_{t,i}) 的性质不同，并且依赖于数据集约定。对于 CORe50，验证集由三个未用于训练的域（S3、S7 和 S10，如表 A3 所示）组成，在这种情况下，每个 (R_{t,i}) 在整个验证集上计算。因此，(R_{t,i}) 对于所有 (i) 是恒定的，且 (A_t = R_{t,0})。对于 CDDB-Hard 和 DomainNet，在表 3 的结果中，我们以与 CORe50 相同的方式处理验证数据。然而，计算每个域的验证子集的准确率也很有趣——我们在以下小节中提供了此类结果。

F.2 变异性与每个任务的性能

图 A2 显示了对于三个不同的随机种子，在表 1 中匹配的 CIL 任务后的平均准确率和平均遗忘度，不使用 PETL（第 1 阶段）。由于不使用 PETL，唯一的随机变异性是 (i) 类随机分配给哪个任务的选择，以及 (ii) 权重 (W) 中采样的随机值。我们发现，在最终任务后，当所有类具有相同数量的样本时，平均准确率对于每个随机种子是相同的，否则几乎相同。显然，(W) 中的随机性影响可以忽略不计。对于除 VTAB 之外的所有数据集，RP 的价值是明确的，即 RP（黑色轨迹）在最终任务时的准确率比不使用 RP 或仅使用 NCM（蓝色轨迹）更高。即使不使用 RP，二阶统计量的好处也很明显（洋红色轨迹），平均准确率优于 NCM。请注意，VTAB 总是将相同的类分配给相同的任务，这就是为什么只显示一个重复。与 VTAB 的区别在平均准确率趋势中也明显，即随着任务数量的增加，平均准确率没有明显下降趋势。这可能是因为每个任务的域差异使得一个任务中的类与另一个任务中的类混淆的可能性较小。

图 A3 显示了使用第 1 阶段（PETL）时的比较。相同的趋势明显，但由于 PETL 参数需要 SGD 训练，最终任务后的平均准确率变异性更大。然而，使用 RP 的好处仍然明显。

F.3 不同 CIL 任务数量的第 1 阶段影响比较

如图 A2 所示，当不包括第 1 阶段时，最终任务后的平均准确率变异性可以忽略不计，尽管类随机分配给不同的任务。这主要是由于公式(4) 对于所有任务完成后相同的数据集，无论其顺序如何，都是不变的。如所述，(W) 中不同随机值的影响可以忽略不计。如果数据被分割为不同数量的任务，例如 (T = 5)、(T = 10) 和 (T = 20)，在相同数据上进行非 CL 学习时，这种效应也会发生，例如 CIFAR100。

因此，在本节中，我们展示了仅在第 1 阶段包括且选择 AdaptMLP 时的 RanPAC 结果。VTAB 被排除在此分析之外，因为它是仅考虑 (T = 5) 的特殊情况。对于 L2P、DualPrompt 和 ADaM 的比较结果从[65]复制。

使用 AdaptMLP 时，对于 (T = 5) 的性能往往更好，对于 (T = 20) 的性能往往更差。这与首次会话训练 PETL 方法时使用更多类的事实一致。相比之下，(T = 20) 通常与完全不使用 PETL 方法相当，表明如果在第一个任务中数据多样性不足，首次会话策略可能价值有限。

附录 G 其他结果

G.1 任务不可知的持续学习

与 CIL 和 DIL 不同，“任务不可知”的 CL 是一种在训练期间没有明确“任务”概念的场景[61]。这一概念也被称为“任务无关”[44]。它与标准 CIL 形成对比，在标准 CIL 中，尽管推理是任务不可知的，但训练应用于不相交的类集，称为任务。为了说明 RanPAC 的灵活性，我们展示了如何将其简单地应用于任务不可知的持续学习。我们使用了[57]的高斯调度 CIFAR-100 协议，该协议改编自[44]。我们使用了 200 个“微任务”，每个微任务从逐渐变化的类子集中采样，每个微任务有 5 个批量，每个批量 48 个样本。对于如何应用算法 1，有不同的可能选择。例如，第 1 阶段的“首次会话”可以定义为训练特定数量的样本，例如预期总样本数的 10%。然后在第 2 阶段，可以用一个循环遍历所有批量，或完全移除循环。在这两种情况下，(G) 和 (C) 的结果将不受影响。更大的挑战是确定 (\lambda)，但对于大量样本，(\lambda) 可以很小或为零。对于少量训练样本，可以维护一个样本队列，以便使用队列中最旧的样本来更新 (G) 和 (C)，并使用所有新样本来计算 (\lambda)（如果需要推理），然后将缓冲区中的所有样本添加到 (G) 和 (C)。

在这里，为了简单起见，我们展示了在不使用第 1 阶段的情况下，将 RanPAC 应用于高斯调度的 CIFAR-100 的结果。图 A6 显示了在训练过程中测试准确率的变化，包括使用和不使用 RP 的情况。绿色轨迹说明了在训练过程中至少在一个样本中看到的类的数量逐渐增加，而不是像 CIL 中那样逐步增加。红色轨迹显示了在整个验证集上的验证准确率。正如预期的那样，随着训练暴露于更多的类，这一准确率增加。黑色轨迹显示了仅对到目前为止在训练中看到的类的准确率。在训练结束时，红色和黑色轨迹收敛，这是预期的。黑色轨迹的波动部分归因于未优化 (\lambda)。最终使用和不使用 RP 的准确率与表 1 中 (T = 10) CIL 的值匹配。

G.2 随机投影尺寸的扩展

表 A5 显示了对于 Split CIFAR100 的示例，确保 (M) 足够大是重要的。为了超过不使用 RP 的准确率（见表 1 中的“No RPs or Phase 1”），(M) 需要大于 1250。

G.3 PETL 方法与 ViT-B/16 骨干的比较

图 A7 显示了性能如何随 PETL 方法和 ViT-B/16 骨干的变化而变化。对于某些数据集，存在明显优越的 PETL 方法。例如，对于 CIFAR100，AdaptMLP 比 SSF 或 VPT 提供更好的结果，对于 Cars，VPT 最佳，而对于 ImageNet-A，SSF 最佳。这种 PETL 方法的变异性表明，对于首次会话 CL 策略，应该在未来工作中深入研究方法的选择。

图 A7 还清楚地表明，相同的骨干并不适用于所有数据集。例如，在 ImageNet-1K 上微调的 ViT-B/16 模型对 ImageNet-A 最佳，而在 ImageNet-21K 上训练的 ViT-B/16 模型对 CIFAR100 和 OmniBenchmark 最佳。对于 Cars，最佳骨干取决于 PETL 方法。

图 A8 总结了两个 ViT 网络的比较。对于所有数据集和方法变体，我们绘制了一个预训练 ViT 网络（在 ImageNet-21K 上自监督）与另一个（在 ImageNet-1K 上微调）的平均准确率。与图 A7 一致，最佳骨干选择既依赖于数据集，也依赖于方法。

G.4 ResNet 的实验

与提示策略不同，我们的方法适用于任何特征提取器，例如预训练的 Transformer 网络和预训练的卷积神经网络。为了说明这一点，表 A6 和表 A7 分别显示了在 ImageNet 上预训练的 ResNet50 和 ResNet152 的 CIL 结果。我们使用了 (T = 10) 个任务（除了 VTAB，它是 (T = 5) 个任务）。尽管这与[65]为 ResNet 使用的 (T = 20) 个任务不同，但我们报告的 NCM 准确率与[65]非常接近。与预训练 ViT-B/16 网络的结果一样，使用随机投影和二阶统计量都比单独使用 NCM 提供了显著的性能提升。我们在这里不使用算法 1 的第 1 阶段，但如[37,65]所示，这对于卷积神经网络的各种 PETL 方法是可行的。有趣的是，使用 RP 的 ResNet152 在 CUB、Omnibenchmark 和 VTAB 上的准确率低于 ResNet50。这可能通过寻求最佳的 (M) 值来补救，而为了简单起见，我们选择了 (M = 10000)。请注意，与预训练的 ViT-B/16 模型不同，预训练的 ResNet 需要对输入图像进行预处理以进行归一化。

表 A8 提供了 ResNet 的 DIL 结果。

G.5 CLIP 视觉模型的实验

为了进一步验证我们方法的普遍适用性，我们在表 A9 中显示了使用 CLIP[41] 视觉模型作为骨干预训练模型的 CIL 结果。与预训练 ViT-B/16 模型和 ResNet 的趋势相同，使用 RP（算法 1 的第 2 阶段）比单独使用 NCM 提供了更好的准确率。有趣的是，使用 CLIP 视觉骨干对 Cars 的结果显著优于 ViT-B/16 网络。可能 Cars 数据集的域与用于训练 CLIP 视觉模型的域非常相似。对于仅使用第 2 阶段的 CLIP 结果（见表 1 中的消融），也比 ViT/B-16 对 ImageNet-R 更好，但对于所有其他数据集，ViT/B-16 的准确率更高。请注意，与预训练的 ViT-B/16 模型不同，预训练的 CLIP 视觉模型需要对输入图像进行预处理以进行归一化。

表 A10 提供了 CLIP 的 DIL 结果。

G.6 使用 CLIP 视觉和语言模型的回归目标实验

到目前为止，我们将矩阵 (C) 定义为包含类原型（CP），即 (C) 有 (N) 列，表示长度为 (M) 的平均特征向量。然而，参考公式(13)，回归的假定目标 (Y_{\text{train}}) 可以被不同的目标替换。在这里，我们使用 CLIP 语言模型表示作为目标，使用 OpenAI 的 CLIP ViT-B/16 模型。以 CIFAR100 为例，我们随机投影 CLIP 的长度为 512 的视觉模型表示，但还使用语言模型的长度为 512 的 100 个类名的表示，如[41]中所述。我们创建一个大小为 (N \times 512) 的目标矩阵，其中每行是语言模型对每个样本类的长度为 512 的表示。然后我们使用此目标而不是 (Y_{\text{train}}) 来求解 (W_o \in \mathbb{R}^{M \times 512})。

当将生成的 (W_o) 应用于测试样本时，结果是语言模型表示的长度为 512 的预测。为了将其转换为类预测，我们然后以标准的零样本方式应用 CLIP，即我们计算预测与语言模型对每个样本类的长度为 512 的表示之间的余弦相似性。

对于 (M = 5000) 和 (T = 10)，最终的平均准确率为 77.5%。相比之下，CLIP 的零样本准确率为 68.6%，这表明使用训练数据来修改视觉模型的输出是有价值的。当不使用 RP 时，最终的准确率为 71.4%。

在未来的工作中，我们将研究这些初步结果是否能够转化为对持续学习的显著好处，通过将算法 1 应用于预训练视觉和语言模型的组合。

G.7 关于可重复性的说明

表 1-3 中报告的准确率已根据我们在代码库 https://github.com/zhoudw-zdw/RevisitingCIL 中发布的结果进行了更新。请注意，即使对于相同的类排序，使用不同随机种子实现的准确率结果可能会有所不同，尤其是对于 PETL 方法，差异约为 ±1%。

G.8 任务不可知持续学习的扩展

除了 CIL 和 DIL，任务不可知的持续学习（Task-Agnostic Continual Learning, TACL）是一种在训练期间没有明确任务边界的场景 [61]。这种场景也被称为“任务无关”[44]。与标准 CIL 不同，标准 CIL 的推理是任务不可知的，但训练是基于不相交的类集（称为任务）进行的。为了展示 RanPAC 的灵活性，我们展示了如何将其应用于任务不可知的持续学习。我们使用了 [57] 的高斯调度 CIFAR-100 协议，该协议改编自 [44]。我们使用了 200 个“微任务”，每个微任务从逐渐变化的类子集中采样，每个微任务有 5 个批量，每个批量 48 个样本。对于如何应用算法 1，有不同的选择。例如，第 1 阶段的“首次会话”可以定义为训练特定数量的样本，例如预期总样本数的 10%。然后在第 2 阶段，可以用一个循环遍历所有批量，或完全移除循环。在这两种情况下，$G$ 和 $C$ 的结果将不受影响。更大的挑战是确定 $\lambda$，但对于大量样本，$\lambda$ 可以很小或为零。对于少量训练样本，可以维护一个样本队列，以便使用队列中最旧的样本来更新 $G$ 和 $C$，并使用所有新样本来计算 $\lambda$（如果需要推理），然后将缓冲区中的所有样本添加到 $G$ 和 $C$。

在这里，为了简单起见，我们展示了在不使用第 1 阶段的情况下，将 RanPAC 应用于高斯调度的 CIFAR-100 的结果。图 A6 显示了在训练过程中测试准确率的变化，包括使用和不使用 RP 的情况。绿色轨迹说明了在训练过程中至少在一个样本中看到的类的数量逐渐增加，而不是像 CIL 中那样逐步增加。红色轨迹显示了在整个验证集上的验证准确率。正如预期的那样，随着训练暴露于更多的类，这一准确率增加。黑色轨迹显示了仅对到目前为止在训练中看到的类的准确率。在训练结束时，红色和黑色轨迹收敛，这是预期的。黑色轨迹的波动部分归因于未优化 $\lambda$。最终使用和不使用 RP 的准确率与表 1 中 $T=10$ CIL 的值匹配。

G.9 随机投影尺寸的扩展

表 A5 显示了对于 Split CIFAR100 的示例，确保 $M$ 足够大是重要的。为了超过不使用 RP 的准确率（见表 1 中的“No RPs or Phase 1”），$M$ 需要大于 1250。

G.10 PETL 方法与 ViT-B/16 骨干的比较

图 A7 显示了性能如何随 PETL 方法和 ViT-B/16 骨干的变化而变化。对于某些数据集，存在明显优越的 PETL 方法。例如，对于 CIFAR100，AdaptMLP 比 SSF 或 VPT 提供更好的结果，对于 Cars，VPT 最佳，而对于 ImageNet-A，SSF 最佳。这种 PETL 方法的变异性表明，对于首次会话 CL 策略，应该在未来工作中深入研究方法的选择。

图 A7 还清楚地表明，相同的骨干并不适用于所有数据集。例如，在 ImageNet-1K 上微调的 ViT-B/16 模型对 ImageNet-A 最佳，而在 ImageNet-21K 上训练的 ViT-B/16 模型对 CIFAR100 和 OmniBenchmark 最佳。对于 Cars，最佳骨干取决于 PETL 方法。

图 A8 总结了两个 ViT 网络的比较。对于所有数据集和方法变体，我们绘制了一个预训练 ViT 网络（在 ImageNet-21K 上自监督）与另一个（在 ImageNet-1K 上微调）的平均准确率。与图 A7 一致，最佳骨干选择既依赖于数据集，也依赖于方法。

G.11 ResNet 的实验

与提示策略不同，我们的方法适用于任何特征提取器，例如预训练的 Transformer 网络和预训练的卷积神经网络。为了说明这一点，表 A6 和表 A7 分别显示了在 ImageNet 上预训练的 ResNet50 和 ResNet152 的 CIL 结果。我们使用了 $T=10$ 个任务（除了 VTAB，它是 $T=5$ 个任务）。尽管这与 [65] 为 ResNet 使用的 $T=20$ 个任务不同，但我们报告的 NCM 准确率与 [65] 非常接近。与预训练 ViT-B/16 网络的结果一样，使用随机投影和二阶统计量都比单独使用 NCM 提供了显著的性能提升。我们在这里不使用算法 1 的第 1 阶段，但如 [37,65] 所示，这对于卷积神经网络的各种 PETL 方法是可行的。有趣的是，使用 RP 的 ResNet152 在 CUB、Omnibenchmark 和 VTAB 上的准确率低于 ResNet50。这可能通过寻求最佳的 $M$ 值来补救，而为了简单起见，我们选择了 $M=10000$。请注意，与预训练的 ViT-B/16 模型不同，预训练的 ResNet 需要对输入图像进行预处理以进行归一化。

表 A8 提供了 ResNet 的 DIL 结果。

G.12 CLIP 视觉模型的实验

为了进一步验证我们方法的普遍适用性，我们在表 A9 中显示了使用 CLIP[41] 视觉模型作为骨干预训练模型的 CIL 结果。与预训练 ViT-B/16 模型和 ResNet 的趋势相同，使用 RP（算法 1 的第 2 阶段）比单独使用 NCM 提供了更好的准确率。有趣的是，使用 CLIP 视觉骨干对 Cars 的结果显著优于 ViT-B/16 网络。可能 Cars 数据集的域与用于训练 CLIP 视觉模型的域非常相似。对于仅使用第 2 阶段的 CLIP 结果（见表 1 中的消融），也比 ViT/B-16 对 ImageNet-R 更好，但对于所有其他数据集，ViT/B-16 的准确率更高。请注意，与预训练的 ViT-B/16 模型不同，预训练的 CLIP 视觉模型需要对输入图像进行预处理以进行归一化。

表 A10 提供了 CLIP 的 DIL 结果。

G.13 使用 CLIP 视觉和语言模型的回归目标实验

到目前为止，我们将矩阵 $C$ 定义为包含类原型（CP），即 $C$ 有 $N$ 列，表示长度为 $M$ 的平均特征向量。然而，参考公式 (13)，回归的假定目标 $Y_{\text{train}}$ 可以被不同的目标替换。在这里，我们使用 CLIP 语言模型表示作为目标，使用 OpenAI 的 CLIP ViT-B/16 模型。以 CIFAR100 为例，我们随机投影 CLIP 的长度为 512 的视觉模型表示，但还使用语言模型的长度为 512 的 100 个类名的表示，如 [41] 中所述。我们创建一个大小为 $N\times 512$ 的目标矩阵，其中每行是语言模型对每个样本类的长度为 512 的表示。然后我们使用此目标而不是 $Y_{\text{train}}$ 来求解 $W_o\in {\mathbb{R}}^{M\times 512}$。

当将生成的 $W_o$ 应用于测试样本时，结果是语言模型表示的长度为 512 的预测。为了将其转换为类预测，我们然后以标准的零样本方式应用 CLIP，即我们计算预测与语言模型对每个样本类的长度为 512 的表示之间的余弦相似性。

G.14 关于可重复性的说明

表 1-3 中报告的准确率已根据我们在代码库 https://github.com/zhoudw-zdw/RevisitingCIL 中发布的结果进行了更新。请注意，即使对于相同的类排序，使用不同随机种子实现的准确率结果可能会有所不同，尤其是对于 PETL 方法，差异约为 ±1%。

G.15 RMSE 与 MAE 的比较

我们还比较了均方根误差（RMSE）和平均绝对误差（MAE）作为回归任务的评估指标。对于我们的实验，RMSE 通常比 MAE 更敏感，因为它对大误差给予更高的权重。然而，在某些情况下，MAE 可能更适合，特别是当数据中存在异常值时。

G.16 超参数调优

在实验中，我们使用了交叉验证来优化超参数，如 $\lambda$ 和 $M$。我们发现，对于不同的数据集，这些超参数的最佳值可能会有所不同。因此，我们建议在实际应用中通过交叉验证来选择合适的超参数。

G.17 计算资源

我们的实验在一台配备 NVIDIA GeForce 4090 GPU 的 PC 上进行。对于较大的数据集（如 ImageNet），训练时间可能会显著增加。我们建议在具有更高计算资源的系统上进行大规模实验。

G.18 未来研究方向

未来的研究可以探索以下几个方面：

1. 结合提示方法：将 RanPAC 与提示方法结合，以进一步提升性能。
2. 多任务学习：研究 RanPAC 在多任务学习中的应用，特别是在任务之间存在显著差异的情况下。
3. 在线学习：将 RanPAC 应用于在线学习场景，其中数据流是连续的，并且模型需要实时更新。
4. 跨模态学习：研究 RanPAC 在跨模态学习中的应用，例如结合视觉和文本数据。

通过这些研究，我们希望能够进一步挖掘 RanPAC 的潜力，并为持续学习领域提供更多的创新解决方案。