LoRA-Pro

解读来源：对齐全量微调！这是我看过最精彩的LoRA改进（二） (opens new window)

文章：LoRA-Pro: Are Low-Rank Adapters Properly Optimized? (opens new window)

文章解读

“LoRA-GA”通过梯度SVD来改进LoRA的初始化，从而实现LoRA与全量微调的对齐。当然，从理论上来讲，这样做也只能尽量对齐第一步更新后的 $W_{1}$ ，LoRA-Pro同样是想着对齐全量微调，但它对齐的是每一步梯度，从而对齐整条优化轨迹，这正好是跟LoRA-GA互补的改进点。

对齐全量

LoRA的参数化方式是

\begin{matrix} (1) & W = (W_{0} - A_{0} B_{0}) + A B \end{matrix}

其中 $W_{0} \in R^{n \times m}$ 预训练权重， $A \in R^{n \times r}, B \in R^{r \times m}$ 新引入的训练参数， $A_{0}, B_{0}$ 它们的初始化值。上一节我们说到，全量微调很多时候效果都优于LoRA，所以全量微调就是LoRA最应该对齐的方向。为了定量描述这一点，我们分别写出全量微调和LoRA微调在SGD下的优化公式，结果分别是

\begin{matrix} (2) & W_{t + 1} = W_{t} - η G_{t} \end{matrix}

和

\begin{matrix} (3) & \begin{matrix} A_{t + 1} = A_{t} - η G_{A, t} = A_{t} - η G_{t} B_{t}^{⊤}, B_{t + 1} = B_{t} - η G_{B, t} = B_{t} - η A_{t}^{⊤} G_{t} \\ W_{t + 1} = W_{t} - A_{t} B_{t} + A_{t + 1} B_{t + 1} \approx W_{t} - η (A_{t} A_{t}^{⊤} G_{t} + G_{t} B_{t}^{⊤} B_{t}) \end{matrix} \end{matrix}

其中 $L$ 损失函数， $η$ 学习率，还有 $G_{t} = \frac{\partial L}{\partial W_{t}}$ 、 $G_{A, t} = \frac{\partial L}{\partial A_{t}} = \frac{\partial L}{\partial W_{t}} B_{t}^{⊤} = G_{t} B_{t}^{⊤}$ 及 $G_{B, t} = \frac{\partial L}{\partial B_{t}} = A_{t}^{⊤} \frac{\partial L}{\partial W_{t}} = A_{t}^{⊤} G_{t}$ 。

LoRA-GA的想法是，我们至少要让全量微调和LoRA的 $W_{1}$ 可能相近，于是它最小化目标

\begin{matrix} (4) & \underset{A_{0}, B_{0}}{argmin} {‖ A_{0} A_{0}^{⊤} G_{0} + G_{0} B_{0}^{⊤} B_{0} - G_{0} ‖}_{F}^{2} \end{matrix}

其最优解可以通过对 $G_{0}$ 行SVD求得，这样我们就可以求出最优的 $A_{0}, B_{0}$ 为 $A, B$ 初始化。

逐步对齐

LoRA-Pro的想法更彻底，它希望对齐全量微调和LoRA的每一个 $W_{t}$ 。可是要怎样才能做到这一点呢？难道每一步都要最小化 ${‖ A_{t} A_{t}^{⊤} G_{t} + G_{t} B_{t}^{⊤} B_{t} - G_{t} ‖}_{F}^{2}$ ? 这显然是不对的，因为 $A_{t}, B_{t}$ 由优化器根据 $A_{t - 1}, B_{t - 1}$ 它们的梯度确定的，并不是可自由调节的参数。

看上去已经没有能够让我们修改的地方了？不，LoRA-Pro非常机智地想到：既然“ $A_{t}, B_{t}$ 由优化器根据 $A_{t - 1}, B_{t - 1}$ 它们的梯度确定的”，后面的 $A_{t - 1}, B_{t - 1}$ 梯度我们都没法改，那我们还可以改优化器呀！具体来说，我们将 $A_{t}, B_{t}$ 更新规则改为：

\begin{matrix} (5) & \begin{matrix} A_{t + 1} = A_{t} - η H_{A, t} \\ B_{t + 1} = B_{t} - η H_{B, t} \end{matrix} \end{matrix}

其中 $H_{A, t}, H_{B, t}$ 定，但它们的形状跟 $A, B$ 致。现在可以写出

\begin{matrix} (6) & W_{t + 1} = W_{t} - A_{t} B_{t} + A_{t + 1} B_{t + 1} \approx W_{t} - η (H_{A, t} B_{t} + A_{t} H_{B, t}) \end{matrix}

这时候我们就可以调整 $H_{A, t}, H_{B, t}$ ，让这个 $W_{t + 1}$ SGD的 $W_{t + 1}$ 可能相近了：

\begin{matrix} (7) & \underset{H_{A, t}, H_{B, t}}{argmin} {‖ H_{A, t} B_{t} + A_{t} H_{B, t} - G_{t} ‖}_{F}^{2} \end{matrix}

下面我们来求解这个优化问题。简单起见，在求解过程中我们省略下标 $t$ ，即考虑

\begin{matrix} (8) & \underset{H_{A}, H_{B}}{argmin} {‖ H_{A} B + A H_{B} - G ‖}_{F}^{2} \end{matrix}

简化目标

由于 $H_{A}, H_{B}$ 间没有约束，所以 $H_{A}, H_{B}$ 优化是独立的，因此我们可以采取先优化 $H_{A}$ 优化 $H_{B}$ 策略（当然反过来也可以）。当我们优化 $H_{A}$ ， $H_{B}$ 相当于是常数，为此，我们可以先考虑如下简化的等价命题

\begin{matrix} (9) & \underset{H}{argmin} {‖ H B - X ‖}_{F}^{2} \end{matrix}

其中 $H \in R^{n \times r}, B \in R^{r \times m}, X \in R^{n \times m}$ 。如果 $r = m$ $B$ 逆，那么我们直接可以变为解方程组 $H B = X$ ，即 $H = X B^{- 1}$ 。当 $r < m$ ，我们就要诉诸优化手段，注意到 $H B - X$ 于 $H$ 线性的，所以这实质就是线性回归的最小二乘问题，它是有解析解的，答案是

\begin{matrix} (10) & H = X B^{⊤} (B B^{⊤})^{- 1} \end{matrix}

其中 $B^{⊤} (B B^{⊤})^{- 1}$ 是矩阵 $B$ “伪逆 (opens new window)”。不了解这个答案也不要紧，我们现场推一下。首先，记 $l = {‖ H B - X ‖}_{F}^{2}$ ，直接求 $H$ 导数得到

\begin{matrix} (11) & \frac{\partial l}{\partial H} = 2 (H B - X) B^{⊤} = 2 (H B B^{⊤} - X B^{⊤}) \end{matrix}

然后让它等于零就可以解出式 $(10)$ 。可能有些读者不大了解矩阵求导法则，其实根据求导的链式法则，我们就不难想到 $\frac{\partial l}{\partial H}$ $2 (H B - X)$ $B$ 某种方式相乘起来，然后我们约定 $\frac{\partial l}{\partial H}$ 形状跟 $H$ 样，即 $n \times r$ ，那么由 $2 (H B - X)$ $B$ 乘来凑出一个 $n \times r$ 结果，也只有 $2 (H B - X) B^{⊤}$ 。

同理， ${‖ A H - X ‖}_{F}^{2}$ $H$ 导数就是 $2 A^{⊤} (A H - X)$ ，由此可以得到

\begin{matrix} (12) & \underset{H}{argmin} {‖ A H - X ‖}_{F}^{2} \Rightarrow H = (A^{⊤} A)^{- 1} A^{⊤} X \end{matrix}

完整结果

有了结论 $(10)$ $(12)$ ，我们就可以着手求解 $(8)$ 。首先我们固定 $H_{B}$ ，那么根据式 $(10)$ 到

\begin{matrix} (13) & H_{A} = (G - A H_{B}) B^{⊤} (B B^{⊤})^{- 1} \end{matrix}

注意式 $(8)$ 目标函数具有一个不变性：

\begin{matrix} (14) & {‖ H_{A} B + A H_{B} - G ‖}_{F}^{2} = {‖ (H_{A} + A C) B + A (H_{B} - C B) - G ‖}_{F}^{2} \end{matrix}

其中 $C$ 任意 $r \times r$ 矩阵。也就是说， $H_{A}$ 解可以加/减任意具有 $A C$ 式的矩阵，只需要 $H_{B}$ /加对应的 $C B$ 行。根据该性质，我们可以将式 $(13)$ $H_{A}$ 化成

\begin{matrix} (15) & H_{A} = G B^{⊤} (B B^{⊤})^{- 1} \end{matrix}

代回目标函数得

\begin{matrix} (16) & \underset{H_{B}}{argmin} {‖ A H_{B} - G (I - B^{⊤} (B B^{⊤})^{- 1} B) ‖}_{F}^{2} \end{matrix}

根据式 $(12)$

\begin{matrix} (17) & H_{B} = (A^{⊤} A)^{- 1} A^{⊤} G (I - B^{⊤} (B B^{⊤})^{- 1} B) \end{matrix}

留意到 $G B^{⊤}, A^{⊤} G$ 好分别是 $A, B$ 梯度 $G_{A}, G_{B}$ ，以及再次利用前述不变性，我们可以写出完整的解

\begin{matrix} (18) & {\begin{aligned} H_{A} = & G_{A} (B B^{⊤})^{- 1} + A C \\ H_{B} = & (A^{⊤} A)^{- 1} G_{B} (I - B^{⊤} (B B^{⊤})^{- 1} B) - C B \end{aligned} \end{matrix}

最优参数

至此，我们求解出了 $H_{A}, H_{B}$ 形式，但解不是唯一的，它有一个可以自由选择的参数矩阵 $C$ 。我们可以选择适当的 $C$ ，来使得最终的 $H_{A}, H_{B}$ 备一些我们所期望的特性。

比如，现在 $H_{A}, H_{B}$ 不大对称的， $H_{B}$ 了 $- (A^{⊤} A)^{- 1} G_{B} B^{⊤} (B B^{⊤})^{- 1} B$ 一项，我们可以将它平均分配到 $H_{A}, H_{B}$ ，使得它们更对称一些，这等价于选择 $C = - \frac{1}{2} (A^{⊤} A)^{- 1} G_{B} B^{⊤} (B B^{⊤})^{- 1}$ ：

\begin{matrix} (19) & {\begin{aligned} H_{A} = & [I - \frac{1}{2} A (A^{⊤} A)^{- 1} A^{⊤}] G_{A} (B B^{⊤})^{- 1} \\ H_{B} = & (A^{⊤} A)^{- 1} G_{B} [I - \frac{1}{2} B^{⊤} (B B^{⊤})^{- 1} B] \end{aligned} \end{matrix}

这个 $C$ 是如下两个优化问题的解：

\begin{matrix} (20) & \begin{array}{r} \underset{C}{argmin} ‖ H_{A} B - A H_{B} ‖_{F}^{2} \end{array} \end{matrix}

\begin{matrix} (21) & \begin{array}{r} \underset{C}{argmin} ‖ H_{A} B - G ‖_{F}^{2} + ‖ A H_{B} - G ‖_{F}^{2} \end{array} \end{matrix}

第一个优化目标可以理解为让 $A, B$ 最终效果的贡献尽可能一样，这跟《配置不同的学习率，LoRA还能再涨一点？》 (opens new window)的假设有一定异曲同工之处，第二个优化目标则是让 $H_{A} B$ 、 $A H_{B}$ 尽可能逼近完整的梯度 $G$ 。以 $l = ‖ H_{A} B - A H_{B} ‖_{F}^{2}$ 例，直接求导得

\begin{matrix} (22) & \frac{\partial l}{\partial C} = 4 A^{⊤} (H_{A} B - A H_{B}) B^{⊤} = 4 A^{⊤} [G_{A} (B B^{⊤})^{- 1} B + 2 A C B] B^{⊤} \end{matrix}

令它等于零我们就可以解出同样的 $C$ ，化简过程比较关键的两步是 $[I - B^{⊤} (B B^{⊤})^{- 1} B] B^{⊤} = 0$ 及 $A^{⊤} G_{A} = G_{B} B^{⊤}$ 。

LoRA-Pro选择的 $C$ 有不同，它是如下目标函数的最优解

\begin{matrix} (23) & \underset{C}{argmin} ‖ H_{A} - G_{A} ‖_{F}^{2} + ‖ H_{B} - G_{B} ‖_{F}^{2} \end{matrix}

这样做的意图也很明显： $H_{A}, H_{B}$ 用来取代 $G_{A}, G_{B}$ ，如果在能达到相同效果的前提下，相比 $G_{A}, G_{B}$ 改动尽可能小，不失为一个合理的选择。同样求 $C$ 导数并让其等于零，化简可得

\begin{matrix} (24) & A^{⊤} A C + C B B^{⊤} = - A^{⊤} G_{A} (B B^{⊤})^{- 1} \end{matrix}

现在我们得到关于 $C$ 一个方程，该类型的方程叫做“Sylvester方程 (opens new window)”，可以通过外积符号写出 $C$ 解析解，但没有必要，因为直接数值求解的复杂度比解析解的复杂度要低，所以直接数值求解即可。总的来说，这些 $C$ 选择方案，都是在让 $H_{A}, H_{B}$ 某种视角下更加对称一些，虽然笔者没有亲自做过对比实验，但笔者认为这些不同的选择之间不会有太明显的区别。

一般讨论

我们来捋一捋到目前为止我们所得到的结果。我们的模型还是常规的LoRA，目标则是希望每一步更新都能逼近全量微调的结果。为此，我们假设优化器是SGD，然后对比了同样 $W_{t}$ 全量微调和LoRA所得的 $W_{t + 1}$ ，发现要实现这个目标，需要把更新过程中 $A, B$ 梯度 $G_{A}, G_{B}$ 成上面求出的 $H_{A}, H_{B}$ 。

接下来就又回到优化分析中老生常谈的问题：前面的分析都是基于SGD优化器的，但实践中我们更常用的是Adam，此时要怎么改呢？如果对Adam优化器重复前面的推导，结果就是 $H_{A}, H_{B}$ 的梯度 $G$ 换成全量微调下Adam的更新方向 $U$ 。然而， $U$ 要用全量微调的梯度 $G$ 照Adam的更新规则计算而来，而我们的场景是LoRA，无法获得全量微调的梯度，只有 $A, B$ 梯度 $G_{A}, G_{B}$ 。

不过我们也可以考虑一个近似的方案，前述 $H_{A} B + A H_{B}$ 优化目标就是在逼近 $G$ ，所以我们可以用它来作为 $G$ 近似来执行Adam，这样一来整个流程就可以走通了。于是我们可以写出如下更新规则

\begin{matrix} (25) & \begin{array}{l} \begin{matrix} G_{A} = \frac{\partial L}{\partial A_{t - 1}}, G_{B} = \frac{\partial L}{\partial B_{t - 1}} \end{matrix} \\ \begin{matrix} H_{A} = G_{A} (B B^{⊤})^{- 1} \\ H_{B} = (A^{⊤} A)^{- 1} G_{B} (I - B^{⊤} (B B^{⊤})^{- 1} B) \\ \tilde{G} = H_{A} B + A H_{B} \end{matrix}} 估计梯度 \\ \begin{matrix} M_{t} = β_{1} M_{t - 1} + (1 - β_{1}) \tilde{G} \\ V_{t} = β_{2} V_{t - 1} + (1 - β_{2}) {\tilde{G}}^{2} \\ {\hat{M}}_{t} = \frac{M_{t}}{1 - β_{1}^{t}}, {\hat{V}}_{t} = \frac{V_{t}}{1 - β_{2}^{t}}, U = \frac{{\hat{M}}_{t}}{\sqrt{{\hat{V}}_{t} + ϵ}} \end{matrix}} Adam更新 \\ \begin{matrix} U_{A} = U B^{⊤}, U_{B} = A^{⊤} U \\ {\tilde{H}}_{A} = U_{A} (B B^{⊤})^{- 1} + A C \\ {\tilde{H}}_{B} = (A^{⊤} A)^{- 1} U_{B} (I - B^{⊤} (B B^{⊤})^{- 1} B) - C B \end{matrix}} 投影到 A, B \\ \begin{matrix} A_{t} = A_{t - 1} - η {\tilde{H}}_{A} \\ B_{t} = B_{t - 1} - η {\tilde{H}}_{B} \end{matrix} \end{array} \end{matrix}

这也是LoRA-Pro最终所用的更新算法（更准确地说，LoRA-Pro用的是AdamW，结果稍复杂一些，但并无实质不同）。然而，且不说如此改动引入的额外复杂度如何，这个算法最大的问题就是它里边的滑动更新变量 $M, V$ 全量微调一样都是满秩的，也就是说它的优化器相比全量微调并不省显存，仅仅是通过低秩分解节省了参数和梯度的部分显存，这相比常规LoRA的显存消耗还是会有明显增加的。

一个比较简单的方案（但笔者没有实验过）就是直接用 $H_{A}, H_{B}$ 代 $G_{A}, G_{B}$ ，然后按照常规LoRA的Adam更新规则来计算，这样 $M, V$ 形状就跟相应的 $A, B$ 致了，节省的显存达到了最大化。不过此时的Adam理论基础不如LoRA-Pro的Adam，更多的是跟《对齐全量微调！这是我看过最精彩的LoRA（一）》 (opens new window)一样，靠“SGD的结论可以平行应用到Adam”的信仰来支撑。

实验结果

LoRA-Pro在GLUE上的实验结果更加惊艳，超过了全量微调的结果：

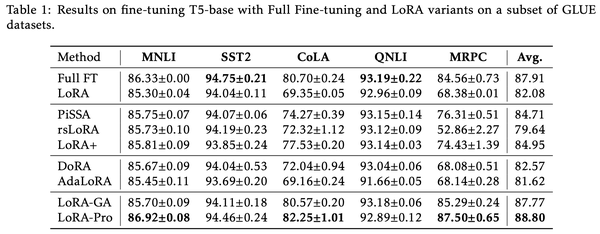
不过论文也就只有这个实验了。看上去LoRA-Pro成文比较仓促，可能是看到LoRA-GA后觉得“撞车”感太明显，所以先赶出来占个坑吧。笔者刚刷到LoRA-Pro时，第一反应也是跟LoRA-GA撞车了，但仔细阅读之下才发现，它跟LoRA-GA实际上是同一思想下互补的结果。

从LoRA-Pro的结果来看，它包含了 $A^{⊤} A$ $B B^{⊤}$ 求逆，所以很明显 $A, B$ 一就不能用全零初始化了，比较符合直觉的正交初始化，即让初始的 $A^{⊤} A, B B^{⊤}$ 单位阵（的若干倍）。刚好从《对齐全量微调！这是我看过最精彩的LoRA（一）》 (opens new window)我们可以看到，LoRA-GA给出的初始化正好是正交初始化，所以LoRA-Pro跟LoRA-GA可谓是“最佳搭档”了。

文章小结

本文介绍了另一个对齐全量微调的工作LoRA-Pro，它跟上一篇的LoRA-GA正好是互补的两个结果，LoRA-GA试图通过改进初始化来使得LoRA跟全量微调对齐，LoRA-Pro则更彻底一些，它通过修改优化器的更新规则来使得LoRA的每一步更新都尽量跟全量微调对齐，两者都是非常精彩的LoRA改进，都是让人赏心悦目之作。

ChatGPT全文翻译 ⬇️

0. 摘要

低秩适应（LoRA）已成为通过将原始矩阵重新参数化为两个低秩矩阵的乘积来进行参数高效微调基础模型的主要方法。尽管其效率较高，但 LoRA 的性能通常不如完整微调。本文提出了一种方法，称为 LoRA-Pro，以缩小这种性能差距。

首先，我们深入研究了 LoRA 和完整微调的优化过程。我们揭示了尽管 LoRA 采用低秩近似，但它忽略了完整微调的优化过程。为了解决这一问题，我们引入了一个新概念，称为“等效梯度”，该虚拟梯度使重新参数化矩阵的优化过程等效于 LoRA，并可用于量化 LoRA 与完整微调之间的差异。等效梯度是从矩阵 A 和 B 的梯度推导出的。为了缩小性能差距，我们的方法在优化过程中最小化等效梯度与从完整微调中获得的梯度之间的差异。通过解决该目标，我们推导出更新矩阵 A 和 B 的最优闭合解。我们的方法约束了优化过程，缩小了 LoRA 与完整微调之间的性能差距。

在自然语言处理任务上的广泛实验验证了我们方法的有效性。

1. 引言

基础模型 [1-5] 已经成为现代深度学习的基石。通过在大规模数据集上进行预训练，这些模型通常表现出卓越的泛化能力和多功能性。令人瞩目的是，某些基础模型甚至展示了突现属性 [6-7]。因此，基础模型已广泛应用于各种下游任务。

尽管这些优势明显，但基础模型庞大的参数数量限制了它们的广泛应用。庞大的参数量使得这些任务的微调成本非常高。为了应对此问题，近期研究集中在参数高效微调（PEFT）方法 [8-11]。PEFT 方法通过冻结基础模型并仅微调小规模的轻量化适配器，降低了微调成本。在大多数参数被冻结的情况下，PEFT 实现了更快的微调，并且需要更少的计算资源。

低秩适应 [8]，也称为 LoRA，是最著名的 PEFT 方法之一，已在各个领域得到广泛采用。受以往工作的启发 [12-13]，LoRA 假设模型适应过程中权重的变化表现出低秩结构。为了捕捉这一点，LoRA 通过将这些变化表示为两个低秩矩阵的乘积来重新参数化它们： $W = W_{0} + Δ W \approx W_{0} + s B A$ ，其中 $s$ 是一个缩放因子， $A \in R^{r \times n}$ 和 $B \in R^{m \times r}$ 是秩为 $r ≪ min (m, n)$ 的低秩矩阵。LoRA 将可训练的参数数量从 $m \times n$ 减少到 $r \times (m + n)$ ，从而降低了微调成本。然而，尽管 LoRA 效率高，它的微调性能通常不如完整微调 [8, 14-16]。

本文提出了一种新型 PEFT 方法，称为 LoRA-Pro，旨在缩小 LoRA 与完整微调之间的性能差距。尽管 LoRA 通过重新参数化权重变化为两个低秩矩阵的乘积来进行低秩近似，但它未能在优化过程中逼近完整微调。为了衡量它们在优化过程中的差异，我们提出了一种新颖的概念，即 LoRA 优化的“等效梯度”。等效梯度描述了低秩近似后原始矩阵的梯度（尽管它不可直接训练），由矩阵 A 和 B 的梯度组成。因此，在 LoRA 微调过程中，我们的目标不仅是用低秩矩阵逼近原始矩阵，还要在梯度下降过程中最小化等效梯度与完整微调梯度之间的差异。这是通过为矩阵 A 和 B 选择合适的梯度来实现的，确保微调过程更加准确和高效。为此，我们将其形式化为一个优化问题，然后推导出该问题的理论解，给出更新矩阵 A 和 B 的最优梯度解。这些解确保等效梯度与完整微调的优化动态密切匹配。通过这种方式，我们增强了 LoRA 的有效性，缩小了 LoRA 与完整微调之间的性能差距。

我们的主要贡献总结如下：

我们发现 LoRA 逼近了低秩矩阵，但未能逼近完整参数微调的优化过程。这一缺陷是 LoRA 与完整微调之间性能差距的原因之一。
我们引入了等效梯度的概念，使我们能够量化 LoRA 与完整微调之间的优化过程差异。通过最小化这种差异，我们推导出了 LoRA 的最优闭合更新解。
在自然语言处理任务上的广泛实验验证了我们方法的有效性。

2. 相关工作

2.1 参数高效微调

由于基础模型的巨大规模，近年来的研究重点集中在开发参数高效的微调方法 [8-11, 14-16]。这些方法旨在通过只调整模型的一小部分参数来降低微调的成本。通常，这些方法可以分为两类。

第一类是适配器微调 [9, 10, 17-20]，其核心思想是在模型的特定层中插入一些小型的神经网络模块，称为适配器。在微调过程中，模型的主体部分保持冻结，只有轻量化的适配器模块被微调，从而显著减少了微调的内存占用。

第二类是提示微调 [11, 21-24]。提示微调通过在输入数据中添加专门设计的提示或可学习的标记来适应特定任务，而不是直接修改基础模型的内部参数。

本文我们关注的是低秩适应（LoRA） [8]，它是适配器微调领域内一个著名的方法。

2.2 低秩适应

低秩适应，最初称为 LoRA [8]，已演变为一个广泛的类别，涵盖基于低秩近似的参数高效微调方法 [8, 14-16, 25-33]。LoRA 假设预训练模型权重的变化表现出低秩结构。因此，它将这些变化重新参数化为低秩矩阵的乘积，从而减少了微调的成本。

针对该方法的不同方面，已经提出了多个 LoRA 的变体。例如，DoRA [14] 通过引入一个可学习的幅度向量来重新缩放低秩矩阵的归一化乘积，从而改进了 LoRA [8]。另一个变体 rsLoRA [27] 引入了一个新的缩放因子，以稳定高秩场景下的训练。LoRA+ [28] 通过对两个低秩矩阵应用不同的学习率，进一步改进了 LoRA。此外，Galore [33] 通过将完整参数训练的梯度投影到低秩空间，减少了预训练和微调过程中的内存占用。

3. 方法

在本节中，我们首先回顾 LoRA [8]（第 3.1 节）。接下来，我们从优化的角度对比了 LoRA 和完整微调（第 3.2 节）。最后，在第 3.3 节中，我们指出 LoRA 在优化过程中未能逼近完整微调，并提出 LoRA-Pro 作为解决方案，以缩小这一性能差距。

3.1 回顾低秩适应

首先，让我们回顾一下低秩适应（LoRA） [8]。LoRA 的核心思想围绕着识别标准微调过程中变化矩阵 $Δ W$ 的低秩结构展开。这个洞见使得 LoRA [8] 可以将变化矩阵重新参数化为两个低秩矩阵的乘积：

\begin{matrix} (1) & W = W_{0} + Δ W = W_{0} + s B A \end{matrix}

这里， $W_{0} \in R^{m \times n}$ 表示预训练的权重矩阵， $B \in R^{m \times r}$ 和 $A \in R^{r \times n}$ 是低秩矩阵， $s$ 是缩放因子。对于 LoRA [8]， $s = \frac{α}{r}$ ，而对于 rsLoRA [

27]， $s = \frac{α}{\sqrt{r}}$ 。这里， $α$ 是超参数， $r ≪ min (m, n)$ 表示秩。因此，LoRA 将微调参数的数量从 $m \times n$ 大幅减少至 $r \times (m + n)$ 。

3.2 LoRA 与完整微调的比较

尽管 LoRA 在多个领域得到了广泛的应用，但其性能仍然不如完整微调。在本节中，我们回顾并比较了 LoRA 和完整微调的优化过程。在完整微调中，我们使用微分来分析损失变化与权重变化之间的关系：

\begin{matrix} (2) & d L = ⟨ \frac{\partial L}{\partial W}, d W ⟩_{F} \end{matrix}

其中， $d L$ 和 $d W$ 分别表示参数 $W$ 和损失 $L$ 的变化， $∥ \cdot ∥_{F}$ 是 Frobenius 范数。为了最小化损失函数，我们通常设置 $d W = - \frac{\partial L}{\partial W} \equiv - g$ （为简化省略学习率），这导致 $d L = - ∥ \frac{\partial L}{\partial W} ∥_{F}^{2} \leq 0$ 。

在 LoRA 优化中，给定 $W = W_{0} + s B A$ ，我们使用链式法则计算微分：

\begin{matrix} (3) & d L = ⟨ \frac{\partial L}{\partial W}, d W ⟩_{F} = ⟨ \frac{\partial L}{\partial W}, {\frac{\partial W}{\partial A}}^{T} d A + {\frac{\partial W}{\partial B}}^{T} d B ⟩_{F} = ⟨ \frac{\partial L}{\partial A}, d A ⟩_{F} + ⟨ \frac{\partial L}{\partial B}, d B ⟩_{F} \end{matrix}

类似地，LoRA 设置 $d A = - \frac{\partial L}{\partial A} \equiv - g_{A}^{LoRA}$ 和 $d B = - \frac{\partial L}{\partial B} \equiv - g_{B}^{LoRA}$ ，因此 $d L = - ∥ \frac{\partial L}{\partial A} ∥_{F}^{2} - ∥ \frac{\partial L}{\partial B} ∥_{F}^{2} \leq 0$ 。进一步地，通过链式法则我们推导出：

\begin{matrix} (4) & g_{A}^{LoRA} = \frac{\partial L}{\partial W} \frac{\partial W}{\partial A} = s B^{T} g, g_{B}^{LoRA} = \frac{\partial L}{\partial W} \frac{\partial W}{\partial B} = s g A^{T} \end{matrix}

3.3 等效梯度的低秩适应

定义 3.1（等效梯度）

在 LoRA 优化的背景下，我们定义等效梯度为：

\begin{matrix} (5) & \tilde{g} \equiv {\frac{\partial W}{\partial A}}^{T} g_{A} + {\frac{\partial W}{\partial B}}^{T} g_{B} = s B g_{A} + s g B A \end{matrix}

其中， $s$ 是缩放因子， $g_{A}$ 和 $g_{B}$ 分别是 A 和 B 的梯度。

从公式 (3) 中我们可以看到，矩阵 A 和 B 的变化通过链式法则与矩阵 W 的变化紧密相连：

\begin{matrix} (6) & d W = {\frac{\partial W}{\partial A}}^{T} d A + {\frac{\partial W}{\partial B}}^{T} d B = - (s B g_{A}^{LoRA} + s g_{B}^{LoRA} A) \end{matrix}

相比于完整微调，这相当于使用等效梯度 $\tilde{g} = s B g_{A}^{LoRA} + s g_{B}^{LoRA} A$ 来更新 W。然而，在 LoRA 的优化过程中，这一关键关系被忽视了。因此，我们假设通过精心调整 A 和 B 的梯度，使得 LoRA 下的等效梯度 $\tilde{g}$ 能够逼近完整微调的梯度 $g$ ，就可以有效地缩小 LoRA 与完整微调之间的性能差距。

基于这一关系，我们在定义 1 中引入了等效梯度的概念。等效梯度描述了低秩适应后矩阵 W 的梯度，尽管 W 不是可训练的参数。为了缩小性能差距，我们的目标是精心选择合适的 $g_{A}$ 和 $g_{B}$ ，以最小化等效梯度 $\tilde{g}$ 和完整微调梯度 $g$ 之间的距离。因此，我们的目标函数为：

\begin{matrix} (7) & min_{g_{A}, g_{B}} ∥ \tilde{g} - g ∥_{F}^{2} s.t. \tilde{g} = s B g_{A} + s g B A, d L \leq 0 \end{matrix}

定理 3.1

假设矩阵 $B \in R^{m \times r}$ 和 $A \in R^{r \times n}$ 都是满秩的。对于目标函数 $min_{g_{A}, g_{B}} ∥ \tilde{g} - g ∥_{F}^{2}$ ，其解为：

\begin{matrix} (8) & g_{A} = \frac{1}{s} (B^{T} B)^{- 1} B^{T} g + X_{A} = \frac{1}{s^{2}} (B^{T} B)^{- 1} g_{A}^{LoRA} + X_{A} \end{matrix}

\begin{matrix} (9) & g_{B} = \frac{1}{s} [I - B (B^{T} B)^{- 1} B^{T}] g A^{T} (A A^{T})^{- 1} - B X = \frac{1}{s^{2}} [I - B (B^{T} B)^{- 1} B^{T}] g_{B}^{LoRA} (A A^{T})^{- 1} - B X \end{matrix}

其中， $X \in R^{r \times r}$ 是一个任意矩阵。

闭式解

幸运的是，目标函数 (7) 有一个闭式解。根据定理 3.1，我们得到了更新矩阵 A 和 B 的最优梯度，确保等效梯度能够最好地逼近完整微调的梯度。此外，我们还发现 $g_{A}$ 和 $g_{B}$ 可以分别表示为 $g_{A}^{LoRA}$ 和 $g_{B}^{LoRA}$ ，这表明我们并不显式地拥有完整微调的梯度 $g$ 。因此，我们的方法是在 LoRA 的标准反向传播中调整 A 和 B 的梯度，并使用定理 3.1 中的闭式解来进行更新。

定理 3.2

在使用定理 3.1 的闭式解更新矩阵 A 和 B 时，我们的更新步骤如下：

\begin{matrix} (10) & A \leftarrow A - γ g_{A} \end{matrix}

\begin{matrix} (11) & B \leftarrow B - γ g_{B} \end{matrix}

其中， $γ \geq 0$ 表示学习率。我们的方法确保了损失的下降，与标准的梯度下降算法类似，其表达式为：

\begin{matrix} (12) & d L = - γ {⟨ g_{A}^{LoRA}, \frac{1}{s^{2}} (B^{T} B)^{- 1} g_{A}^{LoRA} ⟩_{F} + ⟨ g_{B}^{LoRA}, \frac{1}{s^{2}} [I - B (B^{T} B)^{- 1} B^{T}] g_{B}^{LoRA} (A A^{T})^{- 1} ⟩_{F}} \leq 0 \end{matrix}

尽管定理 3.1 提供了优化问题 $min_{g_{A}, g_{B}} ∥ \tilde{g} - g ∥_{F}^{2}$ 的闭式解，但这并不意味着使用该解更新 A 和 B 就会减少损失。为了解决这一问题，我们有了定理 3.2，它确保在优化过程中损失会减少。该定理表明，损失的变化 $d L$ 可以表达为两个正定二次型的和与一个负标量的乘积。这个关系确保了在更新过程中 $d L \leq 0$ ，从而持续推动优化过程朝着更低的损失前进。

定理 3.3

考虑优化问题：

\begin{matrix} (13) & min_{X} ∥ g_{A} - g_{A}^{LoRA} ∥_{F}^{2} + ∥ g_{B} - g_{B}^{LoRA} ∥_{F}^{2} \end{matrix}

其中， $g_{A}$ 和 $g_{B}$ 是定理 3.1 中的最优解。最优 $X$ 可以通过解 Sylvester 方程得到：

\begin{matrix} (14) & B^{T} B X + X A A^{T} = - \frac{1}{s^{2}} (B^{T} B)^{- 1} g_{A}^{LoRA} A^{T} \end{matrix}

当且仅当 $B^{T} B$ 和 $- A A^{T}$ 没有共享特征值时，该方程有唯一解。

X 的选择

虽然等效梯度本身与矩阵 $X$ 没有直接关系，但 $X$ 在更新矩阵 A 和 B 时起到了重要作用。我们选择适当的 $X$ ，使得 $g_{A}$ 和 $g_{B}$ 分别接近 $g_{A}^{LoRA}$ 和 $g_{B}^{LoRA}$ 。因此，我们最小化它们的 Frobenius 范数，如公式 (13) 所示。在实际操作中， $B^{T} B$ 和 $A A^{T}$ 通常没有共同特征值。因此，根据定理 3.3，我们可以确定唯一的最优 $X$ 来更新矩阵 A 和 B。

4. 实验结果

在本节中，我们评估了我们提出的 LoRA-Pro 方法在多个自然语言理解数据集上的表现。为了提供全面的对比，我们包含了以下基线方法：1）完整微调和标准 LoRA [8]；2）保持原始结构的 LoRA 变体，如 rsLoRA [27]、LoRA+ [28]、PiSSA [34]；3）结构上有改动的 LoRA 变体，包括 DoRA [14] 和 AdaLoRA [35]。

结果如表 1 所示。我们在 GLUE 数据集的一个子集上微调了 T5-base 模型 [36]。从表 1 中可以看出，LoRA-Pro 在 5 个数据集中的 3 个数据集上取得了最高分数，并且在所有 5 个数据集上的平均得分也最高。此外，平均来看，LoRA-Pro 相较于标准 LoRA [8] 提升了 6.72 分。这些结果验证了我们方法的有效性。

表 1：在 GLUE 数据集的子集上使用 T5-base 进行微调的结果（完整微调和 LoRA 变体）。

方法	MNLI	SST2	CoLA	QNLI	MRPC	平均分数
完整微调	86.33±0.00	94.75±0.21	80.70±0.24	93.19±0.22	84.56±0.73	87.91
LoRA	85.30±0.04	94.04±0.11	69.35±0.05	92.96±0.09	68.38±0.01	82.08
PiSSA	85.75±0.07	94.07±0.06	74.27±0.39	93.15±0.14	76.31±0.51	84.71
rsLoRA	85.73±0.10	94.19±0.23	72.32±1.12	93.12±0.09	52.86±2.27	79.64
LoRA+	85.81±0.09	93.85±0.24	77.53±0.20	93.14±0.03	74.43±1.39	84.95
DoRA	85.67±0.09	94.04±0.53	72.04±0.94	93.04±0.06	68.08±0.51	82.57
AdaLoRA	85.45±0.11	93.69±0.20	69.16±0.24	91.66±0.05	68.14±0.28	81.62
LoRA-GA	85.70±0.09	94.11±0.18	80.57±0.20	93.18±0.06	85.29±0.24	87.77
LoRA-Pro	86.92±0.08	94.46±0.24	82.25±1.01	92.89±0.12	87.50±0.65	88.80

5. 结论

在本文中，我们提出了 LoRA-Pro，一种旨在缩小 LoRA 与完整微调之间性能差距的新方法。为此，我们引入了“等效梯度”的概念，它使我们能够量化 LoRA 与完整微调在优化过程中的差异。通过最小化这种差异，我们推导出了 LoRA 的最优闭式更新解。此外，我们证明了这些解在优化过程中确保了损失的减少。这些解不仅对微调矩阵进行了低秩近似，还保持了与完整微调优化的一致性，从而实现了更有效的微调。最后，我们通过在自然语言处理任务上的广泛实验验证了我们方法的有效性。

上次更新: 2025/06/25, 11:25:50

← LoRA-GA LoRA+→