文章来源：机器学习方法—优雅的模型（一）：变分自编码器（VAE） (opens new window)

1. Introduction

2. Motivation

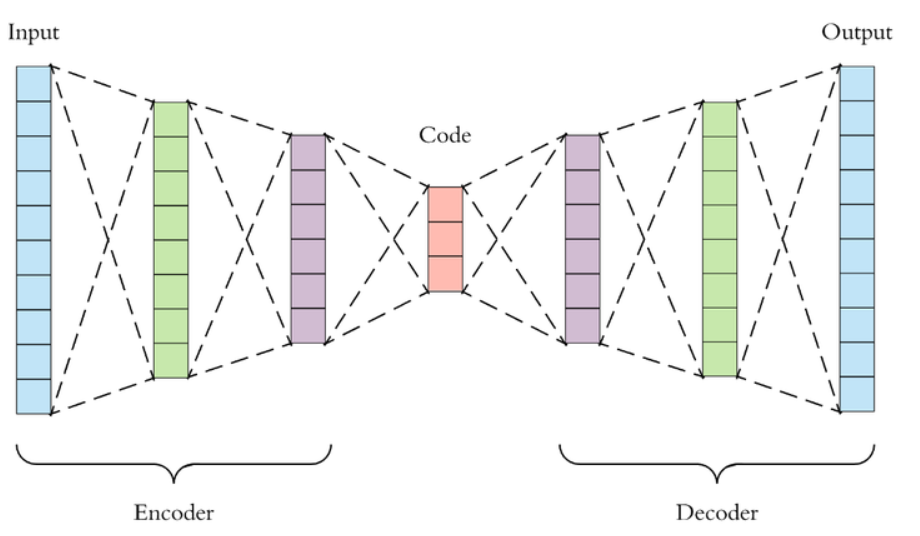
在说 VAE 之前，自然要先说到传统的自编码器 (Autoencoder)。上图即是一个自编码的实例。自编码器类似于一个非线性的 PCA，是一个利用神经网络来给复杂数据降维的模型。现在我们记$X$ 整个数据集的集合，$x_i$ 数据集中的一个样本。

自编码器包含一个编码器$z=g(X)$，它的输出$z$ 们称作编码，$z$ 维度往往远远小于输入$X$ 维度。它还包含一个解码器$\tilde{X}=f(z)$，这个解码器能够通过编码$z$ 到$\tilde{X}。$

我们希望解码器解码得到的$\tilde{X}$ 够尽可能的接近$X，$ 以自编码器一个常用的损失函数是$\ell =\parallel X-\tilde{X}{\parallel }^2。$ 样一来，模型训练结束后，我们就可以认为编码$z$ 括了输入数据$X$ 大部分信息，也因此我们可以直接利用$z$ 达原始数据，从而达到数据降维的目的。

出于方便，假设现在我们的输入$X\in {\mathbb{R}}^{C\times H\times W}$ 一些图片，我们可以训练一个自编码器。它的编码器$z=g(X)$ 每个图片编码成$z\in {\mathbb{R}}^d，$ 的解码器$\tilde{X}=f(z)$ 用$z$ 输入的图片重建为$\tilde{X}\in {\mathbb{R}}^{C\times H\times W}$。

我们现在仔细研究一下这个模型的解码器$g:{\mathbb{R}}^d\to {\mathbb{R}}^{C\times H\times W}。$ 个解码器只需要输入某些低维向量$z，$ 能够输出高维的图片数据$X。$ 我们能否把这个模型直接当做生成模型，在低维空间${\mathbb{R}}^d$ 随机生成某些向量$z$，再喂给解码器$f(z)$ 生成图片呢？

答案是，我们可以这么做，运气好的话我们可以得到一些有用的图片，但是对绝大多数随机生成的$z$，$f(z)$ 会生成一些没有意义的噪声。

为什么会这样呢？这是因为我们没有显性的对$z$ 分布$p(z)$ 行建模，我们并不知道哪些$z$ 够生成有用的图片。我们用来训练$f(z)$ 数据是有限的，$f$ 能只会对极有限的$z$ 响应。而${\mathbb{R}}^d$ 是一个太大的空间，如果我们只在这个空间上随机采样的话，我们自然不能指望总能恰好采样到能够生成有用的图片的$z。$

在 Autoencoder 的基础上，显性的对$z$ 分布$p(z)$ 行建模，使得自编码器成为一个合格的生成模型，我们就得到了 Variational Autoencoders，即今天的主题，变分自编码器。

3. Derivation

我们在这一章正式对 VAE 进行推导。对于自编码器来说，$z$ 分布是不确定的，因此只能在${\mathbb{R}}^d$ 采样、碰运气。我们为什么不给定$z$ 个简单的分布，将采样的空间缩的很小呢？

我们不妨假设$z\sim \mathcal{N}(0,I)，$ 中$I$ 表一个单位矩阵。也就是说，我们将$z$ 作是一个服从标准多元高斯分布的多维随机变量。

现在我们记$z$、$X$ 随机变量，$z_i$、$x_i$ 表随机变量的样本。

在这个架构下，我们可以认为数据集是由某个随机过程生成的，而$z$ 这个随机过程中的一个不可观测到的隐变量。这个生成数据的随机过程包含两个步骤：

1. 从先验分布$p(z)$ 采样得到一个$z_i$
2. 根据$z_i，$ 条件分布$p(X\mid z_i)$ 采样得到一个数据点$x_i$

如果我们能基于这个随机过程进行建模，那么我们可能可以更轻易的得到一个生成模型。

3.1 Decoder

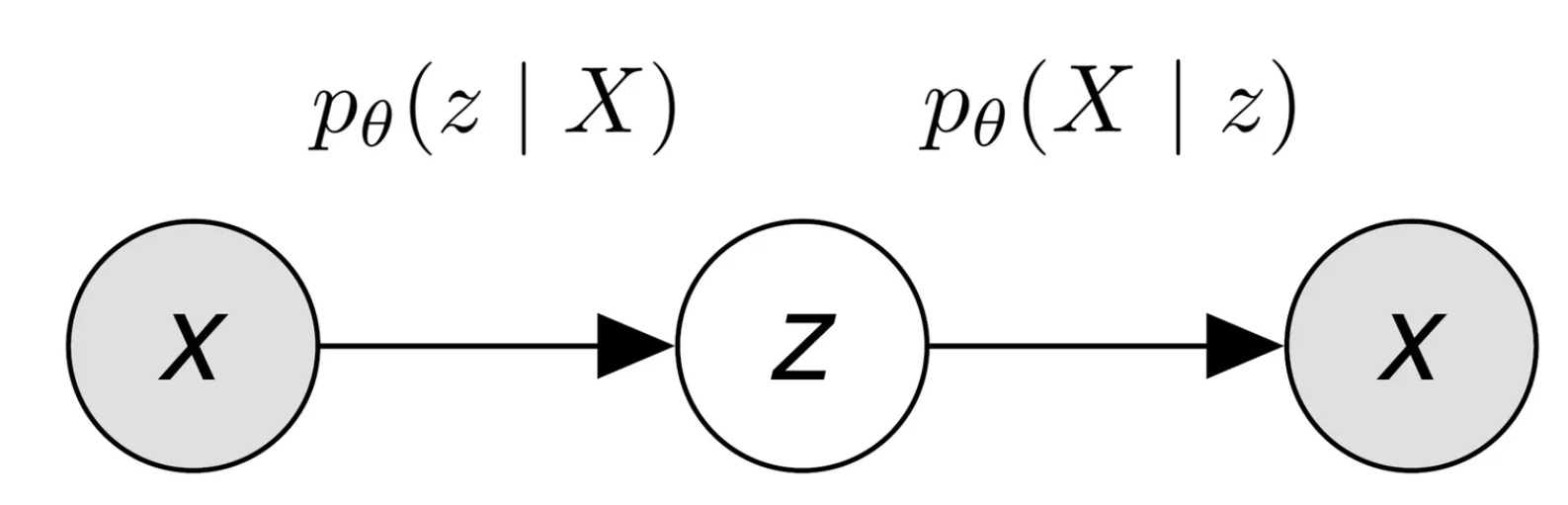
首先，让我们从生成模型的角度来考虑 Decoder 的架构。

上图是一个 Decoder 架构的示意图。我们给 Decoder 输入一个从$\mathcal{N}(0,I)$ 采样得到的$z_i，$ 实是希望由$\theta$ 数化的 Decoder 能够学会一个映射，输出$z_i$ 应的$X$ 分布，即$p_{\theta }(X\mid z_i)。$

让我们假设，给定任意$z_i$ ，$X$ 服从某个各维度独立的多元高斯分布，即：

$$p_{\theta }(X\mid z_i)=\mathcal{N}(X\mid {\mu }_i^{\prime }(z_i;\theta ),{\sigma }_i^{\prime 2}(z_i;\theta )\ast I).$$

这样一来，我们只需要输入$z_i$ Decoder，然后让它拟合出${\mu }_i^{\prime }\mathrm{和}{\sigma }_i^{\prime 2}，$ 们就能知道$X \mid z_i $ 具体分布了。

我们举个例子来更直观的理解这个过程。我们根据分布$p(z)$ 样出一个$z_i，$ 个$z_i$ 当对应图片集$X$ 的某一部分类似的图片。比如说，我们的图片集$X$ 能是世界上所有的猫，那么抽样得到的一个$z_i$ 能代表颜色为橘色，耳朵为立耳的猫；而下次抽样得到的另一个$z_j$ 能代表颜色为白色，耳朵为折耳的猫。

我们再假设，在这个$z_i$ ，这类立耳橘猫的图片像素值的分布$X\mid z_i$ 从一个多元高斯分布$\mathcal{N}({\mu }_i^{\prime },{\sigma }_i^{\prime 2}\ast I)。$ 样一来，我们的 Decoder 只需要通过神经网络，将$z_i$ 换为适当的${\mu }_i^{\prime }\mathrm{和}{\sigma }_i^{\prime 2}，$ 们就得到了这个多元高斯分布。之后我们就可以从$\mathcal{N}({\mu }_i^{\prime },{\sigma }_i^{\prime 2}\ast I)$ 采样，得到立耳橘猫的图片了！

3.2 Objective

因为本质上我们希望训练一个生成模型，我们也不妨以一个更加统计的视角来看一个生成模型的目标函数。

对于一个生成模型，我们的终极目标是什么？对，我们就是想对数据本身的分布$p(X)$ 行建模。如果能成功得到一个逼近真实分布$p(X)$ $p_{\theta }(X)，$ 么我们就能从中进行采样，生成一些可能的数据点。

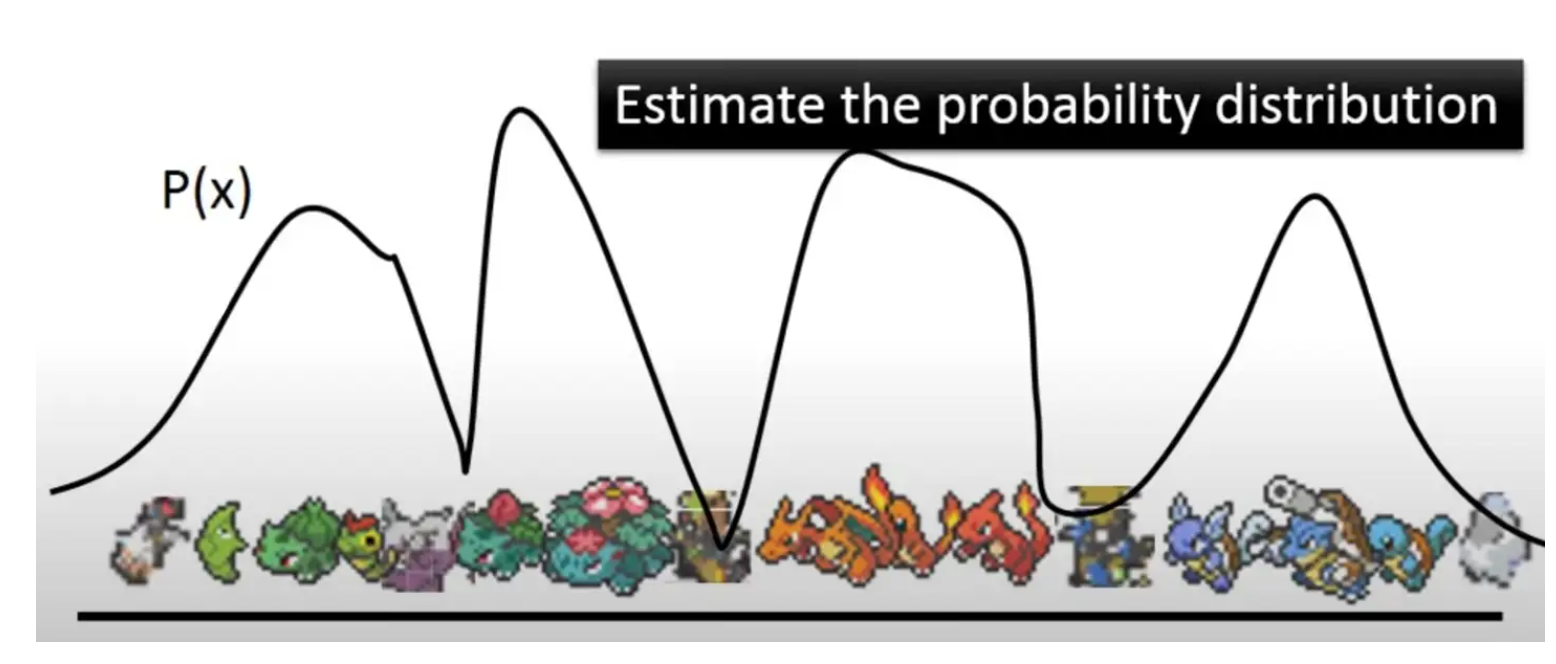
如上图，我们举个当$X$ 表所有宝可梦的图片的例子。在得到$p_{\theta }(X)$ ，我们就可以生成一些令$p_{\theta }(x_i)$ 较大的$x_i$，这些$x_i$ 很可能会是正常的宝可梦的图片。

现在的问题就是，我们怎么对$p_{\theta }(X)$ 行建模呢？

有了之前的铺垫，现在我们有$$p(z) = \mathcal{N}(0, I)，p_{\theta}(X \mid z) = \mathcal{N}(X \mid \mu_i^{\prime}(z; \theta), \sigma_i^{\prime2}(z; \theta) * I)。$$ 得，

$$\begin{array}{rl}{p}_{\theta }(X)& ={\int }_z{p}_{\theta }(X\mid z)p(z)dz\\ & \approx \frac{1}{m}\sum _{j=1}^m{p}_{\theta }(X\mid z_j).\end{array}$$

这样问题是不是就解决了呢？我们只要从$p(z)=\mathcal{N}(z\mid 0,I)$ 采样许多$z_i$ 来，就能算出$p_{\theta }(X)。$ 之前的文章机器学习理论—统计：MLE 与 MAP (opens new window)中，我们已经介绍过了 MLE。在这里，我们就可以利用 MLE 的思想，让数据集出现的概率最大化，也就是：

$$\begin{array}{rl}{\theta }^{\ast }& ={\mathrm{argmin}}_{\theta }-\sum _{i=1}^n\log p_{\theta }(x_i)\\ & ={\mathrm{argmin}}_{\theta }-\sum _{i=1}^n\log (\frac{1}{m}\sum _{j=1}^m{p}_{\theta }(x_i\mid z_j)).\end{array}$$

我们确实可以这样做，但是这样做的代价是极大的。因为往往$x_i$ 维度会很大，$z_i$ 维度也不会很低，并且，对于某个$x_i$ 言，与之强相关的$z_i$ 数量是相对有限的，但是为了找到这些有限的$z_i，$ 们可能要进行大量的采样。

所以如果我们希望较为准确的估计$p_{\theta }(X)$ 话，我们可能需要采样极大量的$z_i$，只有这样，我们才能让模型知道究竟哪一些$z_i$ 与哪一些$x_i$ 应着的。

因此，直接从$p(z)$ 采样$z_i，$ 来估计$p_{\theta }(X)$ 策略几乎是不可行的。不过解决这个问题的思路也很直觉，那就是在 Encoder 中引入后验分布$p_{\theta }(z\mid x_i)。$

3.3 Encoder

具体来说，我们怎么在 Encoder 中利用后验分布呢？假设我们现在有后验分布$p_{\theta }(z\mid x_i)，$ 样的话，如下图，每次前向传播的时候，我们可以先将$x_i$ 给 Encoder，算出$z\mid x_i$ 从的分布。之后，我们就可以直接在这个分布中采样出$z_i，$ 给 Decoder，然后得到$X\mid z_i$ 分布，最后基于 MLE 优化模型。

在这个策略下，从$p_{\theta }(z\mid x_i)$ 采样出来的$z_i$ 乎都会和$x_i$ 关的，对比之前，我们可能就省去了很多采样的步骤，极大的提高了效率。

那现在的问题就是，我们怎么计算$p_{\theta }(z\mid x_i)$ ？我们不妨先尝试下贝叶斯公式：

$$\begin{array}{rl}{p}_{\theta }(z\mid x_i)& =\frac{p_{\theta }(x_i\mid z)p(z)}{p_{\theta }(x_i)}\\ & =\frac{p_{\theta }(x_i\mid z)p(z)}{{\int }_{\hat{z}}{p}_{\theta }(x_i\mid \hat{z})p(\hat{z})d\hat{z}}.\end{array}$$

辛运的是，我们之前已经假设了$p_{\theta }(X\mid z)\mathrm{和}p(z)$ 分布，所以对于上式的分子，我们是可以直接算出来的。不幸的是，上式的分母又有一个积分，如果去估计这个积分的话，又会需要从$p(z)$ 采样大量的$z_i。$ 显然是代价极大，不太可行的。

这时候我们就可以应用变分贝叶斯算法了！我们不妨令由$\varphi$ 数化的 Encoder 去拟合对任意$x_i$ 分布$q_{\varphi }(z\mid x_i)，$ 们希望这个分布能够尽可能的逼近真实的后验分布$p_{\theta }(z\mid x_i)。$ 果$q_{\varphi }(z\mid x_i)$ 够足够逼近真实的后验分布的话，我们就可以直接通过 Encoder 得到$z\mid x_i$ 分布了！

我们怎么用神经网络去拟合后验分布呢？和之前一样，我们只要知道这个后验是服从的什么分布，然后让模型拟合这个分布所需的参数就行了。举个例子，如果这个后验分布本质上是一个多元高斯分布，那么我们让 Encoder 输出$\mu$ ${\mathrm{\Sigma }}^2$ 能拟合这个分布了。

回忆一下，我们之前已经对似然$p_{\theta }(X\mid z)$ 先验$p(z)$ 分布做了假设——它们都服从高斯分布。在这种情况下，不难证明，真实的后验分布$p_{\theta }(z\mid X)$ 服从高斯分布。

那不妨令近似后验分布对任意$x_i$ 有

$$q_{\varphi }(z\mid x_i)=\mathcal{N}(z\mid \mu (x_i;\varphi ),{\sigma }^2(x_i;\varphi )\ast I)$$

即，它也是一个各维度独立的多元高斯分布。这样一来，整个 VAE 的架构就非常明了了。

3.4 Architecture

下图即是 VAE 的架构示例。其中$x_i^{(j)}$ 表第$i$ 数据点的第$j$ 特征。

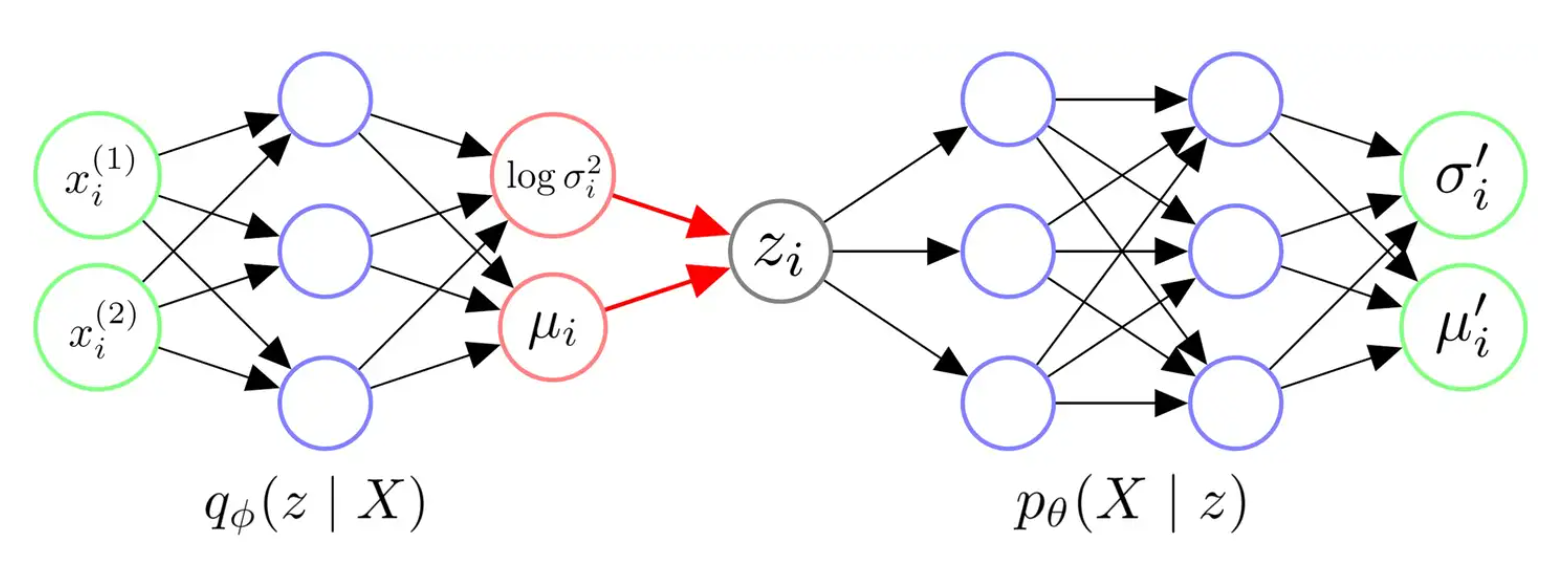
总结一下 VAE 的架构：

1. 我们首先给 Encoder 输入一个数据点$x_i，$ 过神经网络，我们得到隐变量$z$ 从的近似后验分布$q_{\varphi }(z\mid x_i)$ 参数。我们往往认为后验分布是一个各维度独立的高斯分布，因此令 Encoder 输出$z\mid x_i$ 从的高斯分布的参数${\sigma }_i^2$ ${\mu }_i$ 可。
2. 有了$z\mid x_i$ 布的参数${\sigma }_i^2$ ${\mu }_i$ ，我们从对应的高斯分布中采样出一个$z_i，$ 个$z_i$ 当代表与$x_i$ 似的一类样本。
3. 我们令 Decoder 拟合似然的分布$p_{\theta }(X\mid z_i)。$ 给 Decoder 一个$z_i，$ 应当返回$X\mid z_i$ 从的分布的参数。我们往往认为似然也服从一个各维度独立的高斯分布，因此令 Decoder 输出$X\mid z_i$ 从的高斯分布的参数${\sigma }_i^{\prime 2}$ ${\mu }_i^{\prime }$ 可。
4. 在得到$X\mid z_i$ 分布的参数后，理论上我们需要从这个分布中进行采样，来生成可能的数据点$x_i$。

上述第四点中值得注意的是，在大部分实现中，人们往往不进行采样，而是直接将模型输出的${\mu }_i^{\prime }$ 作是给定$z_i$ 成的数据点$x_i。$

除此之外，人们也往往认为$p_{\theta }(X\mid z_i)$ 一个固定方差的各维度独立的多元高斯分布，即$p_{\theta }(X\mid z_i)=\mathcal{N}(X\mid {\mu }_i^{\prime }(z_i;\theta ),{\sigma }^{\prime 2}\ast I)，$ 中${\sigma }^{\prime 2}$ 一个人为给定的超参数。这意味着我们实际中并不真的让模型输出${\sigma }_i^{\prime 2}，$ 型只要输出${\mu }_i^{\prime }$ 行了。

3.5 Reparameterization Trick

上述 VAE 的架构应该是比较清晰的，但让我们再仔细研究一下这个架构。尽管现在我们还没有推导得到最终的损失函数，但让我们先假设，在上述步骤 4 后，我们会接某个损失函数$\mathcal{L}$ 训练神经网络。

这样的话，从神经网络训练的角度来看，这个架构的前向传播过程是没有问题的，上述步骤 1-4 均可顺利的进行前向传播，然后计算出损失的值。

然而，令人在意的一个问题是：我们在前向传播的第 2 步，居然调用了一个"采样函数"，从$z\mid x_i$ 采样出来了$z_i$ 给 Decoder！那采样函数能够进行反向传播吗？

答案显然是不能的。因此，为了让整个网络能够正常的训练，作者们提出了 Reparameterization Trick。这一技巧将上述第 2 步改为：

1. 有了$z\mid x_i$ 布的参数${\sigma }_i^2$ ${\mu }_i$ ，我们先从$\mathcal{N}(0,I)$ 采样得到一个${ϵ}_i$，然后我们令$z_i={\mu }_i+{\sigma }_i\odot {ϵ}_i，$ 个$z_i$ 当代表与$x_i$ 似的一类样本。

其中，$\odot$ 表逐元素相乘操作。不难证明，此时$z_i$ 后的分布依然是由${\sigma }_i^2$ ${\mu }_i$ 数化的一个高斯分布。

利用了 Reparameterization Trick 后，VAE 的架构变成了下图中的模样，其中${ϵ}_i$ 以看作是伴随$z_i$ 给 Decoder 的一个特征。这样一来，这个架构的前向、反向传播就都能跑通了。

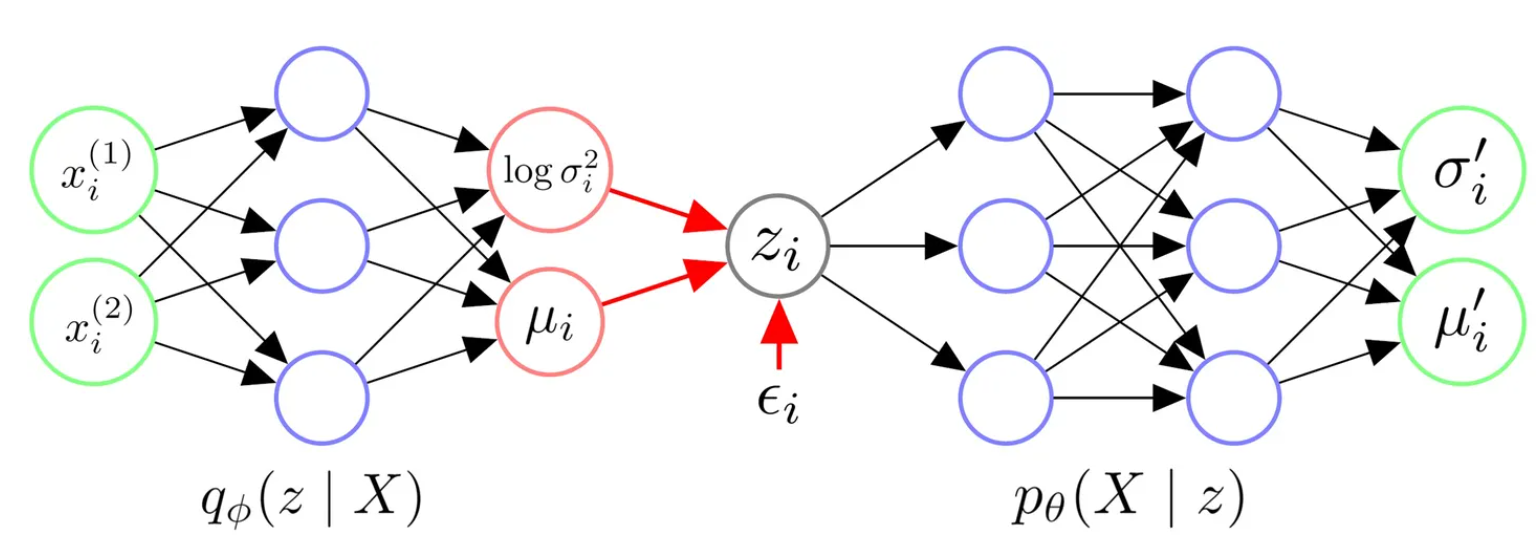
3.6 Evidence Lower Bound

好了，我们已经把 VAE 的架构定下来了。现在我们只要顺着 3.2 节中 MLE 的思想，然后在最大化$\log p_{\theta }(X)$ ，加入变分推断的思想，引入 ELBO (Evidence Lower Bound)，我们就能得到一个靠谱的目标函数了。

让我们来推一下：

$$\begin{array}{rl}\log p_{\theta }(X)& ={\int }_z{q}_{\varphi }(z\mid X)\log p_{\theta }(X)dz\mathrm{全}\mathrm{概}\mathrm{率}\mathrm{定}\mathrm{理}\\ & ={\int }_z{q}_{\varphi }(z\mid X)\log \frac{p_{\theta }(X,z)}{p_{\theta }(z\mid X)}dz\mathrm{贝}\mathrm{叶}\mathrm{斯}\mathrm{定}\mathrm{理}\\ & ={\int }_z{q}_{\varphi }(z\mid X)\log (\frac{p_{\theta }(X,z)}{q_{\varphi }(z\mid X)}\cdot \frac{q_{\varphi }(z\mid X)}{p_{\theta }(z\mid X)})dz\\ & ={\int }_z{q}_{\varphi }(z\mid X)\log \frac{p_{\theta }(X,z)}{q_{\varphi }(z\mid X)}dz+{\int }_z{q}_{\varphi }(z\mid X)\log \frac{q_{\varphi }(z\mid X)}{p_{\theta }(z\mid X)}dz\\ & =\ell (p_{\theta },q_{\varphi })+D_{KL}(q_{\varphi },p_{\theta })\\ & \ge \ell (p_{\theta },q_{\varphi })KL\mathrm{散}\mathrm{度}\mathrm{非}\mathrm{负}.\end{array}$$

我们已经在之前的文章**机器学习理论—信息论：自信息、熵、交叉熵与 KL 散度 (opens new window)**中的第四章证明了 KL 散度是恒大于等于零的，因此显然上式中$\ell (p_{\theta },q_{\varphi })$ $\log p_{\theta }(X)$ 一个下界，也因此我们称$\ell$ ELBO (Evidence Lower Bound)。

我们不妨在把上式变换一下，易得：

$$\ell (p_{\theta },q_{\varphi })=\log p_{\theta }(X)-D_{KL}(q_{\varphi },p_{\theta }).$$

这个式子实在是太完美了！这个式子告诉我们，我们只需要最大化$\ell ，$ 能最大化$\log p_{\theta }(X)，$ 且最小化$D_{KL}(q_{\varphi },p_{\theta })。$

最大化$\log p_{\theta }(X)$ 理由是显然的，因为我们希望最大化似然。我们为什么希望最小化$D_{KL}(q_{\varphi },p_{\theta })$ ？其实原因也是显然的，因为我们希望近似后验$q_{\varphi }(z\mid X)$ 够逼近真实后验$p_{\theta }(z\mid X)，$ 则的话 Encoder 可能只能输出一些无意义的分布。

既然我们希望最大化$\ell ，$ 在我们进一步对其进行展开，不难得到：

$$\begin{array}{rl}\ell (p_{\theta },q_{\varphi })& ={\int }_z{q}_{\varphi }(z\mid X)\log \frac{p_{\theta }(X,z)}{q_{\varphi }(z\mid X)}dz\\ & ={\int }_z{q}_{\varphi }(z\mid X)\log \frac{p_{\theta }(X\mid z)p(z)}{q_{\varphi }(z\mid X)}dz\mathrm{贝}\mathrm{叶}\mathrm{斯}\mathrm{定}\mathrm{理}\\ & ={\int }_z{q}_{\varphi }(z\mid X)\log \frac{p(z)}{q_{\varphi }(z\mid X)}dz+{\int }_z{q}_{\varphi }(z\mid X)\log p_{\theta }(X\mid z)dz\\ & =-D_{KL}(q_{\varphi },p)+{\mathbb{E}}_{q_{\varphi }}[\log p_{\theta }(X\mid z)].\end{array}$$

让我们再将上述两项分别展开。

首先，让我们看下$-D_{KL}(q_{\varphi },p)$ 一项。人们通常称这一项为 Latent Loss 或者将其看做一个正则项。回忆一下，我们之前已经假设了$q_{\phi}(z \mid X) $ $p(z)$ 服从高斯分布，辛运的是，在这种情况下，我们能够得到$D\ast KL(q\ast \varphi ,p)$ 解析解。

更加幸运的是，我们把它们都设成了各维度独立的高斯分布，所以我们可以直接从一维的情况进行推导：

$$\begin{array}{rl}{D}_{KL}(\mathcal{N}(\mu ,{\sigma }^2)\parallel \mathcal{N}(0,1))& ={\int }_z\frac{1}{\sqrt{2\pi {\sigma }^2}}\exp (-\frac{{(z-\mu )}^2}{2{\sigma }^2})\log \frac{\frac{1}{\sqrt{2\pi {\sigma }^2}}\exp (-\frac{{(z-\mu )}^2}{2{\sigma }^2})}{\frac{1}{\sqrt{2\pi }}\exp (-\frac{z^2}{2})}dz\\ & ={\int }_z(\frac{-{(z-\mu )}^2}{2{\sigma }^2}+\frac{z^2}{2}-\log \sigma )\mathcal{N}(\mu ,{\sigma }^2)dz\\ & =-{\int }_z\frac{{(z-\mu )}^2}{2{\sigma }^2}\mathcal{N}(\mu ,{\sigma }^2)dz+{\int }_z\frac{z^2}{2}\mathcal{N}(\mu ,{\sigma }^2)dz-{\int }_z\log \sigma \mathcal{N}(\mu ,{\sigma }^2)dz\\ & =-\frac{\mathbb{E}\left[{(z-\mu )}^2\right]}{2{\sigma }^2}+\frac{\mathbb{E}\left[z^2\right]}{2}-\log \sigma \\ & =\frac{1}{2}(-1+{\sigma }^2+{\mu }^2-\log {\sigma }^2).\end{array}$$

当它们都是$d$ 高斯分布时，易得：

$$D_{KL}(q_{\varphi }(z\mid X),p(z))=\sum _{j=1}^d\frac{1}{2}(-1+{{\sigma }^{(j)}}^2+{{\mu }^{(j)}}^2-\log {{\sigma }^{(j)}}^2).$$

其中${a^{(j)}}^2$ 表向量$a$ 第$j$ 元素的平方。

至此，最后的问题就是，${\mathbb{E}}_{q_{\varphi }}[\log p_{\theta }(X\mid z)]$ 么求呢？这一项往往被称为 Reconstruction Loss，人们通常从$q_{\varphi }(z\mid X)$ 采样多个$z_i$ 近似求解这一项，即：

$${\mathbb{E}}_{q_{\varphi }}[\log p_{\theta }(X\mid z)]\approx \frac{1}{m}\sum _{i=1}^m\log p_{\theta }(X\mid z_i),$$

其中，$z_i\sim q_{\varphi }(z\mid x_i)=\mathcal{N}(z\mid \mu (x_i;\varphi ),{\sigma }^2(x_i;\varphi )\ast I)。$

现在我们来看$\log p_{\theta }(X\mid z_i)$ 一项怎么展开。我们之前已经假设过$X\mid z_i$ 从一个固定方差的各维度独立的多元高斯分布，即$p_{\theta }(X\mid z_i)=\mathcal{N}(X\mid {\mu }_i^{\prime }(z_i;\theta ),{\sigma }^{\prime 2}\ast I)。$

有了之前的文章损失函数（二）：MSE、0-1 Loss 与 Logistic Loss (opens new window)中的 2.2 节的基础后，我们知道，若假设数据为固定方差的高斯分布，MLE 后得到的目标函数，等价于 MSE。但我们这里还是先把它写开，设每个数据点$x_i$ 维度为$K$，即$X\mid z_i$ 从一个$K$ 高斯分布，易得：

$$\begin{array}{rl}\log p_{\theta }(X\mid z_i)& =\log \frac{\exp (-\frac{1}{2}(X-{\mu }^{\prime }{)}^{\mathrm{T}}{\mathrm{\Sigma }}^{\prime -1}(X-{\mu }^{\prime }))}{\sqrt{(2\pi {)}^k|{\mathrm{\Sigma }}^{\prime }|}}\\ & =-\frac{1}{2}(X-{\mu }^{\prime }{)}^{\mathrm{T}}{\mathrm{\Sigma }}^{\prime -1}(X-{\mu }^{\prime })-\log \sqrt{(2\pi {)}^k|{\mathrm{\Sigma }}^{\prime }|}\\ & =-\frac{1}{2}\sum _{k=1}^K\frac{(X^{(k)}-{\mu }^{\prime (k)}{)}^2}{{\sigma }^{\prime (k)}}-\log \sqrt{(2\pi {)}^K\prod _{k=1}^K{\sigma }^{\prime (k)}}.\end{array}$$

这样，我们就有了最终的损失函数所需要的所有模块了。

3.7 Loss Function

让我们把上一节中的推导整合起来。现在希望最小化损失函数：

$$\begin{array}{rl}\mathcal{L}& =-\frac{1}{n}\sum _{i=1}^n\ell (p_{\theta },q_{\varphi })\\ & =\frac{1}{n}\sum _{i=1}^n{D}_{KL}(q_{\varphi },p)-\frac{1}{n}\sum _{i=1}^n{\mathbb{E}}_{q_{\varphi }}[\log p_{\theta }(x_i\mid z)]\\ & =\frac{1}{n}\sum _{i=1}^n{D}_{KL}(q_{\varphi },p)-\frac{1}{nm}\sum _{i=1}^n\sum _{j=1}^m\log p_{\theta }(x_i\mid z_j).\end{array}$$

上式即是通过从$q_{\varphi }(z\mid x_i)$ 采样$m$ $z_j，$ 逼近${\mathbb{E}}_{q_{\varphi }}[\log p_{\theta }(x_i\mid z)]。$ 许我们会好奇，之前两次我们都说积分太难求了，采样逼近代价太大了，所以不能采样逼近，为什么这里又可以采样逼近了呢？

答案就是：之前我们都只能从$p(z)$ 采样$z_j，$ 样的话，采样到和$x_i$ 关联的$z_j$ 概率实在是很低，所以为了更好的逼近积分只能采样大量的$z_j$，这样的代价自然是极大的；然而，在上式中，我们其实是从$q_{\varphi }(z\mid x_i)$ 采样得到$z_j。$ 着网络的训练，近似后验$q_{\varphi }(z\mid x_i)，$ 快就会比较接近真实的后验分布。这样一来，我们有很大可能能够在有限次数的采样中，采样到与$x_i$ 联的$z_j。$

事实上，从经验来看，从$q_{\varphi }(z\mid x_i)$ 采样$z_j$ 计${\mathbb{E}}_{q_{\varphi }}[\log p_{\theta }(x_i\mid z)]$ 比较高效的。在实践中我们往往对一个$x_i$ 采样一个$z_j$，即$m=1，$ 能达到可观的效果。所以我们可以将损失改写，并继续往下展开：

$$\begin{array}{rl}\mathcal{L}& =\frac{1}{n}\sum _{i=1}^n{D}_{KL}(q_{\varphi },p)-\frac{1}{n}\sum _{i=1}^n\log p_{\theta }(x_i\mid z_i)\\ & =\frac{1}{n}\sum _{i=1}^n\sum _{j=1}^d\frac{1}{2}(-1+{{\sigma }_i^{(j)}}^2+{{\mu }_i^{(j)}}^2-\log {{\sigma }_i^{(j)}}^2)\\ & -\frac{1}{n}\sum _{i=1}^n(-\frac{1}{2}\sum _{k=1}^K\frac{(x_i^{(k)}-{\mu }_i^{\prime (k)}{)}^2}{{\sigma }_i^{\prime (k)}}-\log \sqrt{(2\pi {)}^K\prod _{k=1}^K{\sigma }_i^{\prime (k)}}).\end{array}$$

值得注意的是，我们已经假设了$p_{\theta }(X\mid z_i)$ 任意$z_i$ 是方差固定的各维度独立的$K$ 高斯分布，我们不妨令超参数${\sigma }^{\prime }$ 元素值全为$\frac{1}{2}$ $K$ 向量。这样一来，损失可以改写为：

$$\begin{gathered} \begin{array}{}\text{(1)}& \mathcal{L}=\frac{1}{n}\sum _{i=1}^n\sum _{j=1}^d\frac{1}{2}(-1+{{\sigma }_i^{(j)}}^2+{{\mu }_i^{(j)}}^2-\log {{\sigma }_i^{(j)}}^2)+\frac{1}{n}\sum _{i=1}^n\parallel x_i-{\mu }_i^{\prime }{\parallel }^2. \\ \end{array} \end{gathered}$$

其中，$x_i$ 表第$i$ 样本，是 Encoder 的输入。${\mu }_i$ ${\sigma }_i^2$ Encoder 的输出，代表$z\mid x_i$ 分布的参数。$z_i$ 从$z\mid x_i$ 采样得到的一个样本，它是 Decoder 的输入。${\mu }_i^{\prime }$ Decoder 的输出，代表利用$z_i$ 码后对应的数据点${\tilde{x}}_i。$

到这里，我们终于得到了在假设先验、后验、似然均是高斯分布的情况下，VAE 最终的损失函数。值得一提的是，通常人们采用高斯分布只是因为其简便性。我们也可以根据数据的情况，假设更加复杂分布来推导、训练 VAE。在这种情况下，VAE 可能计算会更加复杂，但也可能会得到更强的表达能力。

4. Conditional VAE

根据上面的推导，我们已经可以训练得到一个原版的 VAE 了。模型训练结束后，我们从$p(z)$ 采样得到$z_i$，再喂给 Decoder，就能生成可能的数据点了。

但这里有个问题，尽管现在我们几乎可以确保从$p(z)$ 采样得到的$z_i，$ 能重建出某个$x_i，$ 是我们无法控制生成的是哪一类$x_i。$

举个 MNIST 手写数字的例子，原版 VAE 只能采样得到$z_i$ 随机生成数字。然而，更多的时候我们可能会希望模型能够生成我们指定的数字。这就引出了 CVAE (Conditional VAE)。

假设我们现在的数据集为$X，$ 们现在希望利用它的标注$Y$ 控制生成的结果。在 MNIST 的场景下，就是我们希望能够告诉 Decoder：我现在想生成一个标注为"7"的数字，你帮我生成一个看看。

CVAE 的思路非常简单，这里我们简单介绍一下。

1. 原来 MLE 是最大化数据集出现的概率，也就是对$p_{\theta }(X)$ 模，那么现在我们需要对$p_{\theta }(X|Y)$ 模。
2. 原来我们对$p(z)$ 行建模，现在对$p(z\mid y_i)$ 模。
3. 原来 Decoder 是对似然$p_{\theta }(X\mid z_i)$ 模，现在即是对$p_{\theta }(X\mid z_i,y_i)$ 模。
4. 原来 Encoder 是对近似后验$q_{\varphi }(z\mid x_i)$ 模，现在则需要对$q_{\varphi }(z\mid x_i,y_i)$ 模。

顺着推导，到最后我们其实只需要让 Encoder 和 Decoder 由$y_i$"参数化"就好。这里做法就很多了，一个直观的做法是将$y_i$ 为 Encoder 和 Decoder 的输入，这样它们不就等于被$y_i$"参数化"了嘛。

5. Implementation

我们在VAE.py (opens new window)中实现了 VAE 和 CVAE。VAE 的实现非常简单，主要就是损失函数的实现。我们在代码中的变量名与该文章中的符号是一致的。

下图是我在 MNIST 上跑的一组示例。

也许我们会注意到，VAE 的实现中，人们往往令 Encoder 输出$\log {\sigma }^2，$ 不直接输出$\sigma 。$ 是因为根据定义，我们必须让模型输出$\sigma \ge 0。$ 于方便，我们通过取对数后再取指数的方法，获得$\sigma 。$ 取平方只是为了计算损失的时候不再需要取平方。

除此之外，在 VAE 损失函数的实现中，有一个更需要注意的地方。我们先把之前推的损失函数抄下来：

$$\mathcal{L}=\frac{1}{n}\sum _{i=1}^n\sum _{j=1}^d\frac{1}{2}(-1+{{\sigma }_i^{(j)}}^2+{{\mu }_i^{(j)}}^2-\log {{\sigma }_i^{(j)}}^2)+\frac{1}{n}\sum _{i=1}^n\parallel x_i-{\mu }_i^{\prime }{\parallel }^2$$

可见，上式中第二部分有一个类似 MSE 的项$\frac{1}{n}\sum _{i=1}^n\parallel x_i-{\mu }_i^{\prime }{\parallel }^2。$ 因此，很多基于 Pytorch 实现 VAE 的 Repo，直接采用F.mse_loss(mu_prime, x, reduction='mean')来计算这一项。这是错误的！

设$x_i$ 维度为$K，$Pytorch 中的F.mse_loss等价于：

$$\frac{1}{nK}\sum _{i=1}^n\parallel x_i-{\mu }_i^{\prime }{\parallel }^2$$

如果单纯的使用 MSE 损失训练模型的话，常数项的改变并不会影响模型的结果。但是在 VAE 中，Reconstruction Loss 这一项的常数项是有意义的。

直观的来说，这一的常数项控制 Reconstruction Loss 和 Latent Loss 之间的权重。如果利用F.mse_loss实现的话，等价于将 Reconstruction Loss 的权重降的很低，Decoder 将无法准确重建$x_i。$

抽象的来说，这一常数项代表 Decoder 拟合的分布$p_{\theta }(X\mid z_i)$ 方差${\sigma }^{\prime 2}$。对于图片生成模型，$K$ 往非常大，比如 MNIST 里$K=28\times 28。$ 白无故的多除以了个$K$ 价于我们将$p_{\theta }(X\mid z_i)$ 方差设的非常大，那它生成的图片全都是噪声也不会令人惊讶。也因此，我们往往在设置超参数${\sigma }^{\prime }$ 时候，必然将其设置的较小。

6. Discussion

VAE 中最老生常谈的问题就是，它为什么生成的图片是模糊的？

我在寻找这个问题的答案的时候，从 Reddit 的一个Post (opens new window)上看到一个高赞回答：

Vanilla VAEs with Gaussian posteriors / priors and factorized pixel distributions aren't blurry, they're noisy. People tend to show the mean value of p(x|z) rather than drawing samples from it. Hence the reported blurry samples aren't actually samples from the model, and they don't reveal the extent to which variability is captured by pixel noise. Real samples would typically demonstrate salt and pepper noise due to independent samples from the pixel distributions.

知乎上也有引用这段话的关于 VAE 的文章 (opens new window)。

这一类回答的意思是：高斯分布假设下，VAE 生成的图像并不模糊，而是因为有噪声。为什么呢？因为我们本应该利用 Decoder 拟合一个高斯分布，然后从这个分布中采样得到$x_i$ 。但是人们偷懒，直接认为拟合出的高斯分布的均值${\mu }^{\prime }$ 是生成的数据$x_i。$ 想，本来 Decoder 告诉你的是给定$z_i$ $X$ 能的分布，你到好，直接把这个分布的均值作为生成的图像了，那能不模糊吗？

知乎上另一类回答说，VAE 产生的图像之所以模糊，就是因为高斯分布的假设，比如回答 1 (opens new window)、回答 2 (opens new window)。这类回答的点在于：如果对$p_{\theta }(X\mid z_i)$ 行高斯分布的假设，那么我们等同于假设数据是一个单峰分布，但是现实中数据往往的多峰 (Multimodal) 的，你用单峰的分布去拟合多峰的分布，那模型只能把多峰进行平均来降低损失了，这样一来，拟合的分布对应的图像，自然也就是模糊的了。

这两类回答看问题的角度是不一样的。但我觉得它们都存在一定的问题，至少不能把我完全说服，我列一下各自可能的疑点：

1. 对于第一类回答：确实，本来让你采样，现在你直接拿分布的均值出来，似乎图片注定会变得模糊。但是给你一个模糊的均值，再给你一个高斯的方差，你去采样不依然很可能是模糊的？
2. 对于第二类答案：我数据肯定是多峰的，但我假设$p_{\theta }(X\mid z_i)$ 单峰的为什么不行？只要我能确保每个$z_i$ 应的$X$ 分布是单峰的不就行了？那这样来看，这个问题的本质是因为模型拟合能力不行，输出隐变量无法捕捉充分的信息，而高斯分布也只是受害者？

综上，目前最能说服我的观点是这样的：

模型拟合能力就是没那么强，模型习得的隐变量就是无法完全对应出单峰的$X$ 。在这种前提下，你再假设是高斯分布，那模型只能把多峰的分布给平均了。所以一个更成功的生成模型，就是允许$X\mid z_i$ 一个更复杂的分布，从而使得模型容错率变高：就算你$z_i$ 应的$X$ 多峰的，我这个复杂的分布也能拟合这个多峰的分布。

至于直接取均值而不采样，故而导致模糊的观点，我觉得只能是非常次要的原因。毕竟你输出的均值就已经是模糊的了，再采样也没有意义。

7. References

[1] Doersch, Carl. "Tutorial on variational autoencoders." arXiv preprint arXiv:1606.05908 (2016).

[2] Slides from UIUC CS446: Machine Learning

[3] https://www.youtube.com/watch?v=8zomhgKrsmQ (opens new window)

[4] Zhao, Shengjia, Jiaming Song, and Stefano Ermon. "Towards deeper understanding of variational autoencoding models." arXiv preprint arXiv:1702.08658 (2017).

TODO

变分自编码器VAE：原来是这么一回事 | 附开源代码

Author: [PaperWeekly]

Link: [https://zhuanlan.zhihu.com/p/34998569]

作者丨苏剑林

单位丨广州火焰信息科技有限公司

研究方向丨NLP，神经网络

个人主页丨kexue.fm

过去虽然没有细看，但印象里一直觉得变分自编码器（Variational Auto-Encoder，VAE）是个好东西。趁着最近看概率图模型的三分钟热度，我决定也争取把 VAE 搞懂。

于是乎照样翻了网上很多资料，无一例外发现都很含糊，主要的感觉是公式写了一大通，还是迷迷糊糊的，最后好不容易觉得看懂了，再去看看实现的代码，又感觉实现代码跟理论完全不是一回事啊。

终于，东拼西凑再加上我这段时间对概率模型的一些积累，并反复对比原论文 Auto-Encoding Variational Bayes，最后我觉得我应该是想明白了。

其实真正的 VAE，跟很多教程说的的还真不大一样，很多教程写了一大通，都没有把模型的要点写出来。于是写了这篇东西，希望通过下面的文字，能把 VAE 初步讲清楚。

分布变换

通常我们会拿 VAE 跟 GAN 比较，的确，它们两个的目标基本是一致的——希望构建一个从隐变量 Z 生成目标数据 X 的模型，但是实现上有所不同。

更准确地讲，它们是假设了服从某些常见的分布（比如正态分布或均匀分布），然后希望训练一个模型 X=g(Z)，这个模型能够将原来的概率分布映射到训练集的概率分布，也就是说，它们的目的都是进行分布之间的变换。

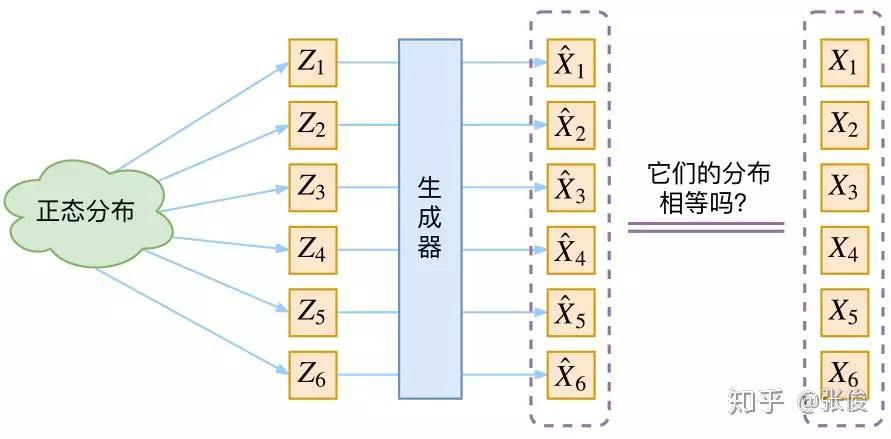
生成模型的难题就是判断生成分布与真实分布的相似度，因为我们只知道两者的采样结果，不知道它们的分布表达式。

那现在假设服从标准的正态分布，那么我就可以从中采样得到若干个 Z1,Z2,…,Zn，然后对它做变换得到 X̂1=g(Z1),X̂2=g(Z2),…,X̂n=g(Zn)，我们怎么判断这个通过 f 构造出来的数据集，它的分布跟我们目标的数据集分布是不是一样的呢？

有读者说不是有 KL 散度吗？当然不行，因为 KL 散度是根据两个概率分布的表达式来算它们的相似度的，然而目前我们并不知道它们的概率分布的表达式。

我们只有一批从构造的分布采样而来的数据 {X̂1,X̂2,…,X̂n}，还有一批从真实的分布采样而来的数据 {X1,X2,…,Xn}（也就是我们希望生成的训练集）。我们只有样本本身，没有分布表达式，当然也就没有方法算 KL 散度。

虽然遇到困难，但还是要想办法解决的。GAN 的思路很直接粗犷：既然没有合适的度量，那我干脆把这个度量也用神经网络训练出来吧。

就这样，WGAN 就诞生了，详细过程请参考http://mp.weixin.qq.com/s?__biz=MzIwMTc4ODE0Mw==&mid=2247484880&idx=1&sn=4b2e976cc715c9fe2d022ff6923879a8&chksm=96e9da50a19e5346307b54f5ce172e355ccaba890aa157ce50fda68eeaccba6ea05425f6ad76&scene=21#wechat_redirect (opens new window)。而 VAE 则使用了一个精致迂回的技巧。

VAE慢谈

这一部分我们先回顾一般教程是怎么介绍 VAE 的，然后再探究有什么问题，接着就自然地发现了 VAE 真正的面目。

经典回顾

首先我们有一批数据样本 {X1,…,Xn}，其整体用 X 来描述，我们本想根据 {X1,…,Xn} 得到 X 的分布 p(X)，如果能得到的话，那我直接根据 p(X) 来采样，就可以得到所有可能的 X 了（包括 {X1,…,Xn} 以外的），这是一个终极理想的生成模型了。

当然，这个理想很难实现，于是我们将分布改一改：

这里我们就不区分求和还是求积分了，意思对了就行。此时 p(X|Z) 就描述了一个由 Z 来生成 X的模型，而我们假设 Z 服从标准正态分布，也就是 p(Z)=N(0,I)。如果这个理想能实现，那么我们就可以先从标准正态分布中采样一个 Z，然后根据 Z 来算一个 X，也是一个很棒的生成模型。

接下来就是结合自编码器来实现重构，保证有效信息没有丢失，再加上一系列的推导，最后把模型实现。框架的示意图如下：

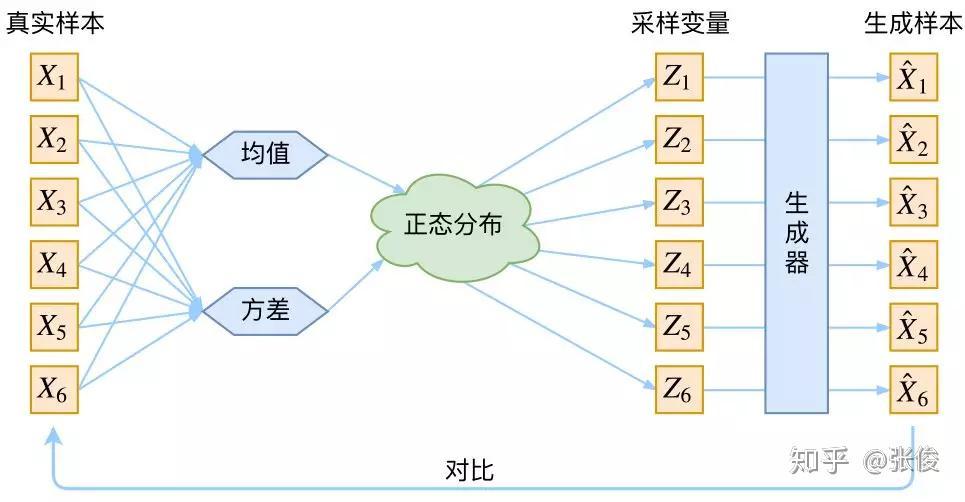
▲ VAE的传统理解

看出了什么问题了吗？如果像这个图的话，我们其实完全不清楚**：究竟经过重新采样出来的Zk，是不是还对应着原来的** Xk，所以我们如果直接最小化 D(X̂ k,Xk)^2（这里 D 代表某种距离函数）是很不科学的，而事实上你看代码也会发现根本不是这样实现的。

也就是说，很多教程说了一大通头头是道的话，然后写代码时却不是按照所写的文字来写，可是他们也不觉得这样会有矛盾。

VAE初现

其实，在整个 VAE 模型中，我们并没有去使用 p(Z)（先验分布）是正态分布的假设，我们用的是假设 p(Z|X)（后验分布）是正态分布。

具体来说，给定一个真实样本 Xk，我们假设存在一个专属于 Xk 的分布 p(Z|Xk)（学名叫后验分布），并进一步假设这个分布是（独立的、多元的）正态分布。

为什么要强调“专属”呢？因为我们后面要训练一个生成器 X=g(Z)，希望能够把从分布 p(Z|Xk) 采样出来的一个 Zk 还原为 Xk。

如果假设 p(Z) 是正态分布，然后从 p(Z) 中采样一个 Z，那么我们怎么知道这个 Z 对应于哪个真实的 X 呢？现在 p(Z|Xk) 专属于 Xk，我们有理由说从这个分布采样出来的 Z 应该要还原到Xk 中去。

事实上，在论文 Auto-Encoding Variational Bayes 的应用部分，也特别强调了这一点：

In this case, we can let the variational approximate posterior be a multivariate Gaussian with a diagonal covariance structure:

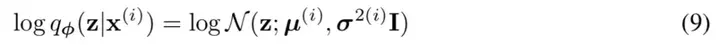
论文中的式 (9) 是实现整个模型的关键，不知道为什么很多教程在介绍 VAE 时都没有把它凸显出来。尽管论文也提到 p(Z) 是标准正态分布，然而那其实并不是本质重要的。

再次强调，这时候每一个 Xk 都配上了一个专属的正态分布，才方便后面的生成器做还原。但这样有多少个 X 就有多少个正态分布了。我们知道正态分布有两组参数：均值 μ 和方差 σ^2（多元的话，它们都是向量）。

那我怎么找出专属于 Xk 的正态分布 **p(Z|Xk) 的均值和方差呢？**好像并没有什么直接的思路。

那好吧，我就用神经网络来拟合出来。这就是神经网络时代的哲学：难算的我们都用神经网络来拟合，在 WGAN 那里我们已经体验过一次了，现在再次体验到了。

于是我们构建两个神经网络 μk=f1(Xk)，logσ^2=f2(Xk) 来算它们了。我们选择拟合 logσ^2 而不是直接拟合 σ^2，是因为 σ^2 总是非负的，需要加激活函数处理，而拟合 logσ^2 不需要加激活函数，因为它可正可负。

到这里，我能知道专属于 Xk 的均值和方差了，也就知道它的正态分布长什么样了，然后从这个专属分布中采样一个 Zk 出来，然后经过一个生成器得到 X̂k=g(Zk)。

现在我们可以放心地最小化 D(X̂k,Xk)^2，因为 Zk 是从专属 Xk 的分布中采样出来的，这个生成器应该要把开始的 Xk 还原回来。于是可以画出 VAE 的示意图：

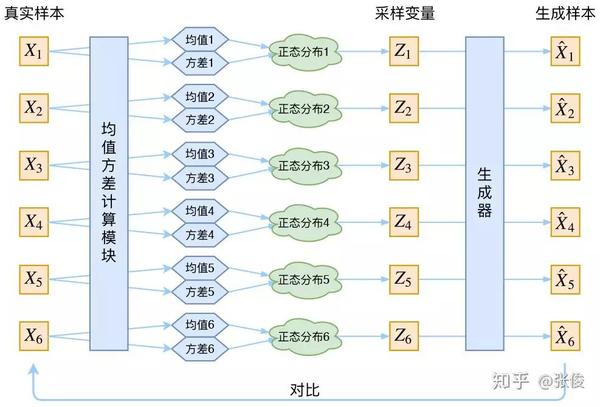
事实上，VAE 是为每个样本构造专属的正态分布，然后采样来重构。

分布标准化

让我们来思考一下，根据上图的训练过程，最终会得到什么结果。

首先，我们希望重构 X，也就是最小化 D(X̂k,Xk)^2，但是这个重构过程受到噪声的影响，因为Zk 是通过重新采样过的，不是直接由 encoder 算出来的。

显然噪声会增加重构的难度，不过好在这个噪声强度（也就是方差）通过一个神经网络算出来的，所以最终模型为了重构得更好，肯定会想尽办法让方差为0。

而方差为 0 的话，也就没有随机性了，所以不管怎么采样其实都只是得到确定的结果（也就是均值），只拟合一个当然比拟合多个要容易，而均值是通过另外一个神经网络算出来的。

说白了，模型会慢慢退化成普通的 AutoEncoder，噪声不再起作用。

这样不就白费力气了吗？说好的生成模型呢？

别急别急，其实 VAE 还让所有的 p(Z|X) 都向标准正态分布看齐，这样就防止了噪声为零，同时保证了模型具有生成能力。

怎么理解“保证了生成能力”呢？如果所有的 p(Z|X) 都很接近标准正态分布 N(0,I)，那么根据定义：

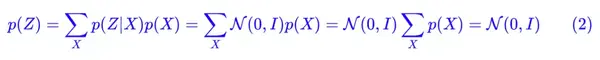
这样我们就能达到我们的先验假设：p(Z) 是标准正态分布。然后我们就可以放心地从 N(0,I) 中采样来生成图像了。

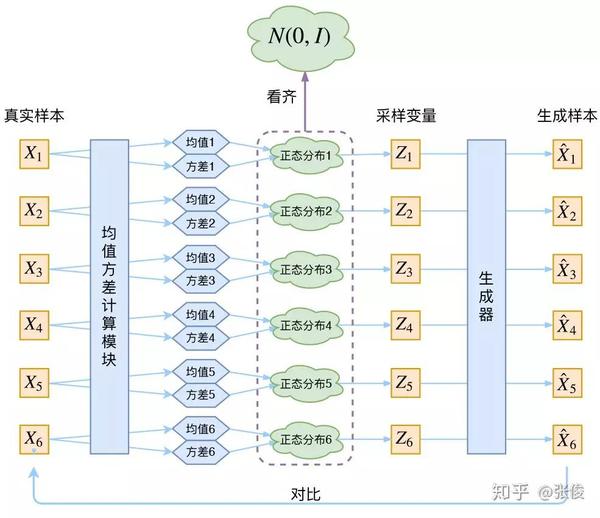
为了使模型具有生成能力，VAE 要求每个 p(Z_X) 都向正态分布看齐。

那怎么让所有的 p(Z|X) 都向 N(0,I) 看齐呢？如果没有外部知识的话，其实最直接的方法应该是在重构误差的基础上中加入额外的 loss：

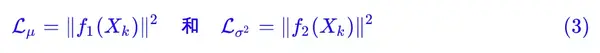
因为它们分别代表了均值 μk 和方差的对数 logσ^2，达到 N(0,I) 就是希望二者尽量接近于 0 了。不过，这又会面临着这两个损失的比例要怎么选取的问题，选取得不好，生成的图像会比较模糊。

所以，原论文直接算了一般（各分量独立的）正态分布与标准正态分布的 KL 散度KL(N(μ,σ^2)‖N(0,I))作为这个额外的 loss，计算结果为：

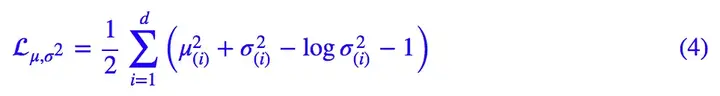
这里的 d 是隐变量 Z 的维度，而 μ(i) 和 σ_{(i)}^{2} 分别代表一般正态分布的均值向量和方差向量的第 i 个分量。直接用这个式子做补充 loss，就不用考虑均值损失和方差损失的相对比例问题了。

显然，这个 loss 也可以分两部分理解：

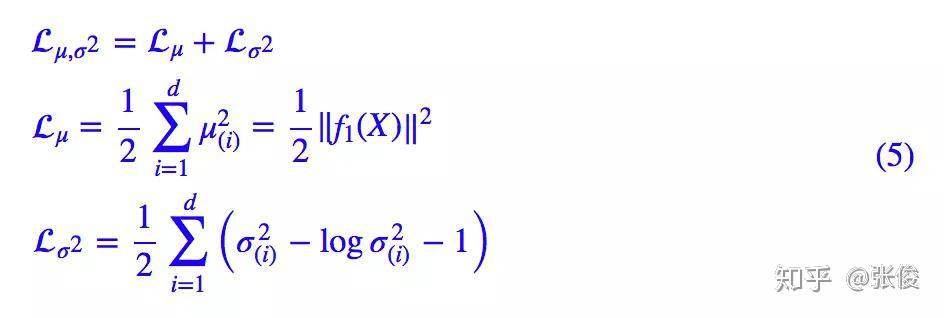
推导

由于我们考虑的是各分量独立的多元正态分布，因此只需要推导一元正态分布的情形即可，根据定义我们可以写出：

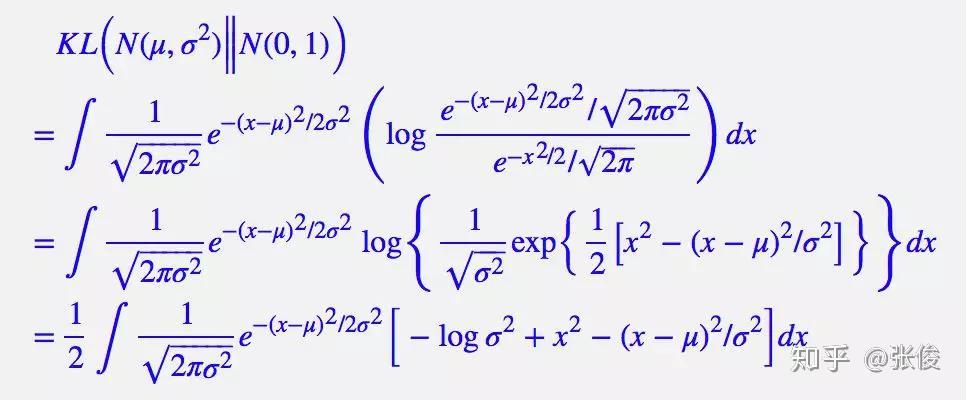
整个结果分为三项积分，第一项实际上就是 −log*σ^2 乘以概率密度的积分（也就是 1），所以结果是 −logσ^*2；第二项实际是正态分布的二阶矩，熟悉正态分布的朋友应该都清楚正态分布的二阶矩为 μ^2+σ^2；而根据定义，第三项实际上就是“-方差除以方差=-1”。所以总结果就是：

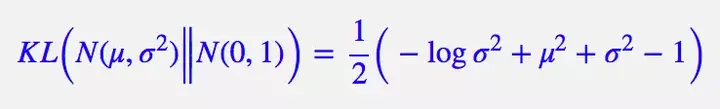
重参数技巧

最后是实现模型的一个技巧，英文名是 Reparameterization Trick，我这里叫它做重参数吧。

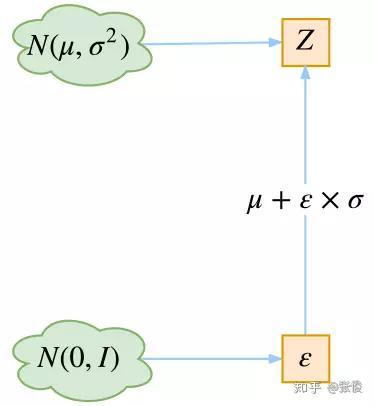
▲ 重参数技巧

其实很简单，就是我们要从 p(Z|Xk) 中采样一个 Zk 出来，尽管我们知道了 p(Z|Xk) 是正态分布，但是均值方差都是靠模型算出来的，我们要靠这个过程反过来优化均值方差的模型，但是“采样”这个操作是不可导的，而采样的结果是可导的，于是我们利用了一个事实：

所以，我们将从 N(μ,σ^2) 采样变成了从 N(μ,σ^2) 中采样，然后通过参数变换得到从N(μ,σ^2) 中采样的结果。这样一来，“采样”这个操作就不用参与梯度下降了，改为采样的结果参与，使得整个模型可训练了。

具体怎么实现，大家把上述文字对照着代码看一下，一下子就明白了。

后续分析

即便把上面的所有内容都搞清楚了，面对 VAE，我们可能还存有很多疑问。

本质是什么

VAE 的本质是什么？VAE 虽然也称是 AE（AutoEncoder）的一种，但它的做法（或者说它对网络的诠释）是别具一格的。

在 VAE 中，它的 Encoder 有两个，一个用来计算均值，一个用来计算方差，这已经让人意外了：Encoder 不是用来 Encode 的，是用来算均值和方差的，这真是大新闻了，还有均值和方差不都是统计量吗，怎么是用神经网络来算的？

事实上，我觉得 VAE 从让普通人望而生畏的变分和贝叶斯理论出发，最后落地到一个具体的模型中，虽然走了比较长的一段路，但最终的模型其实是很接地气的。

它本质上就是在我们常规的自编码器的基础上，对 encoder 的结果（在VAE中对应着计算均值的网络）加上了“高斯噪声”，使得结果 decoder 能够对噪声有鲁棒性；而那个额外的 KL loss（目的是让均值为 0，方差为 1），事实上就是相当于对 encoder 的一个正则项，希望 encoder 出来的东西均有零均值。

那另外一个 encoder（对应着计算方差的网络）的作用呢？它是用来动态调节噪声的强度的。

直觉上来想，当 decoder 还没有训练好时（重构误差远大于 KL loss），就会适当降低噪声（KL loss 增加），使得拟合起来容易一些（重构误差开始下降）。

反之，如果 decoder 训练得还不错时（重构误差小于 KL loss），这时候噪声就会增加（KL loss 减少），使得拟合更加困难了（重构误差又开始增加），这时候 decoder 就要想办法提高它的生成能力了。

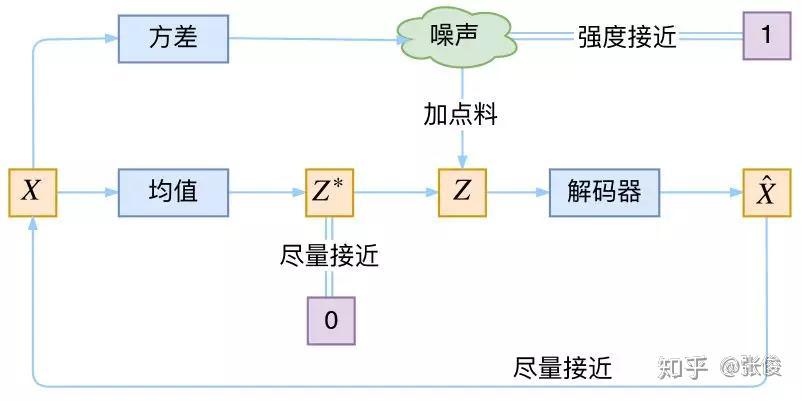
▲ VAE的本质结构

说白了，重构的过程是希望没噪声的，而 KL loss 则希望有高斯噪声的，两者是对立的。所以，VAE 跟 GAN 一样，内部其实是包含了一个对抗的过程，只不过它们两者是混合起来，共同进化的。

从这个角度看，VAE 的思想似乎还高明一些，因为在 GAN 中，造假者在进化时，鉴别者是安然不动的，反之亦然。当然，这只是一个侧面，不能说明 VAE 就比 GAN 好。

GAN 真正高明的地方是：它连度量都直接训练出来了，而且这个度量往往比我们人工想的要好（然而 GAN 本身也有各种问题，这就不展开了）。

正态分布？

对于 p(Z|X) 的分布，读者可能会有疑惑：是不是必须选择正态分布？可以选择均匀分布吗？

首先，这个本身是一个实验问题，两种分布都试一下就知道了。但是从直觉上来讲，正态分布要比均匀分布更加合理，因为正态分布有两组独立的参数：均值和方差，而均匀分布只有一组。

前面我们说，在 VAE 中，重构跟噪声是相互对抗的，重构误差跟噪声强度是两个相互对抗的指标，而在改变噪声强度时原则上需要有保持均值不变的能力，不然我们很难确定重构误差增大了，究竟是均值变化了（encoder的锅）还是方差变大了（噪声的锅）。

而均匀分布不能做到保持均值不变的情况下改变方差，所以正态分布应该更加合理。

变分在哪里

还有一个有意思（但不大重要）的问题是：VAE 叫做“变分自编码器”，它跟变分法有什么联系？在VAE 的论文和相关解读中，好像也没看到变分法的存在？

其实如果读者已经承认了 KL 散度的话，那 VAE 好像真的跟变分没多大关系了，因为 KL 散度的定义是：

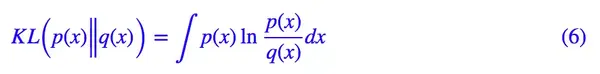
如果是离散概率分布就要写成求和，我们要证明**：已概率分布** p(x)（或固定q(x)）的情况下，对于任意的概率分布 q(x)（或** p(x)），都有 KLp(x)‖q(x))≥0，而且只有当p(x)=q(x)时才等于零**。

因为 KL(p(x)‖q(x))实际上是一个泛函，要对泛函求极值就要用到变分法，当然，这里的变分法只是普通微积分的平行推广，还没涉及到真正复杂的变分法。而 VAE 的变分下界，是直接基于 KL 散度就得到的。所以直接承认了 KL 散度的话，就没有变分的什么事了。

一句话，VAE 的名字中“变分”，是因为它的推导过程用到了 KL 散度及其性质。

条件VAE

最后，因为目前的 VAE 是无监督训练的，因此很自然想到：如果有标签数据，那么能不能把标签信息加进去辅助生成样本呢？

这个问题的意图，往往是希望能够实现控制某个变量来实现生成某一类图像。当然，这是肯定可以的，我们把这种情况叫做 Conditional VAE，或者叫 CVAE（相应地，在 GAN 中我们也有个 CGAN）。

但是，CVAE 不是一个特定的模型，而是一类模型，总之就是把标签信息融入到 VAE 中的方式有很多，目的也不一样。这里基于前面的讨论，给出一种非常简单的 VAE。

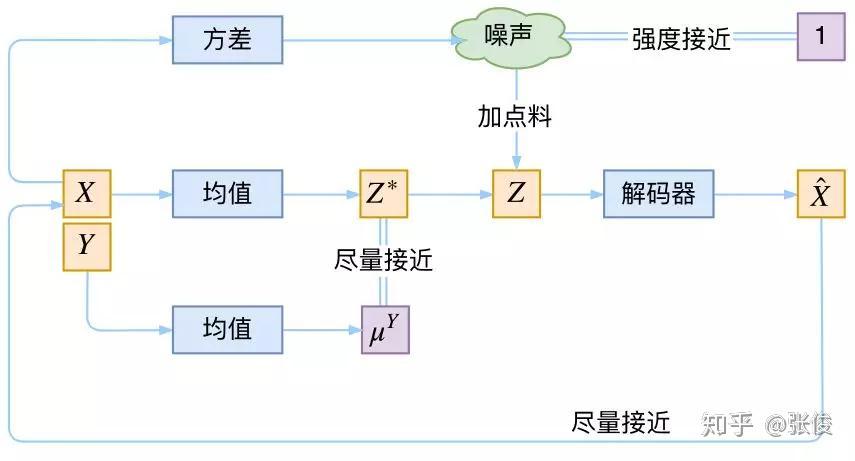
▲ 一个简单的CVAE结构

在前面的讨论中，我们希望 X 经过编码后，Z 的分布都具有零均值和单位方差，这个“希望”是通过加入了 KL loss 来实现的。

如果现在多了类别信息 Y，我们可以希望同一个类的样本都有一个专属的均值 μ^Y（方差不变，还是单位方差），这个 μ^Y 让模型自己训练出来。

这样的话，有多少个类就有多少个正态分布，而在生成的时候，我们就可以通过控制均值来控制生成图像的类别。

事实上，这样可能也是在 VAE 的基础上加入最少的代码来实现 CVAE 的方案了，因为这个“新希望”也只需通过修改 KL loss 实现：

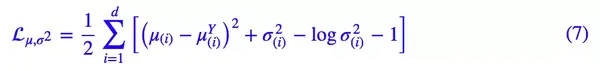
下图显示这个简单的 CVAE 是有一定的效果的，不过因为 encoder 和 decoder 都比较简单（纯 MLP），所以控制生成的效果不尽完美。

用这个 CVAE 控制生成数字 9，可以发现生成了多种样式的 9，并且慢慢向 7 过渡，所以初步观察这种 CVAE 是有效的。

更完备的 CVAE 请读者自行学习了，最近还出来了 CVAE 与 GAN 结合的工作 CVAE-GAN: Fine-Grained Image Generation through Asymmetric Training，模型套路千变万化。

代码

我把 Keras 官方的 VAE 代码复制了一份，然后微调并根据前文内容添加了中文注释，也把最后说到的简单的 CVAE 实现了一下，供读者参考。

代码：https://github.com/bojone/vae (opens new window)

终点站

磕磕碰碰，又到了文章的终点了。不知道讲清楚了没，希望大家多提点意见。

总的来说，VAE 的思路还是很漂亮的。倒不是说它提供了一个多么好的生成模型（因为事实上它生成的图像并不算好，偏模糊），而是它提供了一个将概率图跟深度学习结合起来的一个非常棒的案例，这个案例有诸多值得思考回味的地方。

点击以下标题查看相关内容：

• http://mp.weixin.qq.com/s?__biz=MzIwMTc4ODE0Mw==&mid=2247484093&idx=1&sn=bea0ab9171f2e1ad581ca7869e590dca&chksm=96e9dd3da19e542b17343b0ea30543bd262e92ce26f74491bd509223f5b5d853459981d0f4c7&scene=21#wechat_redirect (opens new window)

• http://mp.weixin.qq.com/s?__biz=MzIwMTc4ODE0Mw==&mid=2247484486&idx=1&sn=d1d84b08626a940bae99db0028e55aae&chksm=96e9dbc6a19e52d02123842cd8c5fa68eeb74bc14142bb3101d7f597699a7d2f3ddf7aba76dd&scene=21#wechat_redirect (opens new window)

本文由 AI 学术社区 PaperWeekly 精选推荐，社区目前已覆盖自然语言处理、计算机视觉、人工智能、机器学习、数据挖掘和信息检索等研究方向，http://www.paperweekly.site/ (opens new window)！

关于PaperWeekly

PaperWeekly 是一个推荐、解读、讨论、报道人工智能前沿论文成果的学术平台。如果你研究或从事 AI 领域，欢迎在公众号后台点击**「交流群」**，小助手将把你带入 PaperWeekly 的交流群里。

微信公众号：PaperWeekly

新浪微博：@PaperWeekly