批量大小对梯度下降法的影响

实际上在计算梯度的时候，并不是对所有数据的损失 $L$ 计算梯度，而是把所有的数据分成一个一个的批量（batch），如图 3.7 所示。每个批量的大小是 $B$ ，即带有 $B$ 笔数据。每次在更新参数的时候，会去取出 $B$ 笔数据用来计算出损失和梯度更新参数。遍历所有批量的过程称为一个回合（epoch）。事实上，在把数据分为批量的时候，我们还会进行随机打乱（shuffle）。随机打乱有很多不同的做法，一个常见的做法是在每一个回合开始之前重新划分批量，也就是说，每个回合的批量的数据都不一样。

假设现在我们有 20 笔训练数据，先看下两个最极端的情况，如图 3.8 所示。

• 图 3.8 （a）的情况是没有用批量，批量大小为训练数据的大小，这种使用全批量（full batch）的数据来更新参数的方法即批量梯度下降法（Batch Gradient Descent，BGD）。此时模型必须把 20 笔训练数据都看完，才能够计算损失和梯度，参数才能够更新一次。
• 图 3.8（b）中，批量大小等于 1，此时使用的方法即随机梯度下降法（Stochastic Gradient Descent，SGD），也称为增量梯度下降法。批量大小等于 1 意味着只要取出一笔数据即可计算损失、更新一次参数。如果总共有 20 笔数据，那么在每一个回合里面，参数会更新 20 次。用一笔数据算出来的损失相对带有更多噪声，因此其更新的方向如图 3.8 所示，是曲曲折折的。

实际上，批量梯度下降并没有“划分批量”：要把所有的数据都看过一遍，才能够更新一次参数，因此其每次迭代的计算量大。但相比随机梯度下降，批量梯度下降每次更新更稳定、更准确。

随机梯度下降的梯度上引入了随机噪声，因此在非凸优化问题中，其相比批量梯度下降更容易逃离局部最小值。

实际上，考虑并行运算，批量梯度下降花费的时间不一定更长；对于比较大的批量，计算损失和梯度花费的时间不一定比使用小批量的计算时间长 。使用 Tesla V100 GPU 在 MNIST数据集得到的实验结果如图 3.9 所示。图 3.9 中横坐标表示批量大小，纵坐标表示给定批量大小的批量，计算梯度并更新参数所耗费的时间。批量大小从 1 到 1000，需要耗费的时间几乎是一样的，因为在实际上 GPU 可以做并行运算，这 1000 笔数据是并行处理的，所以1000笔数据所花的时间并不是一笔数据的 1000 倍。当然 GPU 并行计算的能力还是存在极限的，当批量大小很大的时候，时间还是会增加的。 当批量大小非常大的时候，GPU 在“跑”完一个批量，计算出梯度所花费的时间还是会随着批量大小的增加而逐渐增长 。当批量大小增加到10000，甚至增加到 60000 的时候，GPU 计算梯度并更新参数所耗费的时间确实随着批量大小的增加而逐渐增长。

但是因为有并行计算的能力，因此实际上当批量大小小的时候，要“跑”完一个回合，花的时间是比大的。假设训练数据只有 60000 笔，批量大小设 1，要 60000 个更新才能“跑”完一个回合；如果批量大小等于 1000，60 个更新才能“跑”完一个回合，计算梯度的时间差不多。但60000 次更新跟 60 次更新比起来，其时间的差距量就非常大了。图 3.10(a) 是用一个批量计算梯度并更新一次参数所需的时间。假设批量大小为 1，“跑”完一个回合，要更新 60000 次参数，其时间是非常大的。但假设批量大小是 1000，更新 60 次参数就会“跑”完一个回合。图 3.10(b)是“跑”完一个完整的回合需要花的时间。如果批量大小为 1000 或 60000，其时间比批量大小设 1 还要短 。图 3.10(a) 和图 3.10(b) 的趋势正好是相反的。因此实际上，在有考虑并行计算的时候，大的批量大小反而是较有效率的，一个回合大的批量花的时间反而是比较少的。

大的批量更新比较稳定，小的批量的梯度的方向是比较有噪声的（noisy）。但实际上有噪声的梯度反而可以帮助训练，如果拿不同的批量来训练模型来做图像识别问题，实验结果如图 3.11 所示，横轴是批量大小，纵轴是正确率。图 3.11(a) 是 MNIST 数据集上的结果，图 3.11(b) 是 CIFAR-10 数据集上的结果。批量大小越大，验证集准确率越差。但这不是过拟合，因为批量大小越大，训练准确率也是越低。因为用的是同一个模型，所以这不是模型偏见的题。 但大的批量大小往往在训练的时候，结果比较差。这个是优化的问题，大的批量大小优化可能会有问题，小的批量大小优化的结果反而是比较好的。

一个可能的解释如图 3.12 所示，批量梯度下降在更新参数的时候，沿着一个损失函数来更新参数，走到一个局部最小值点或鞍点显然就停下来了。梯度是零，如果不看海森矩阵，梯度下降就无法再更新参数了 。但小批量梯度下降法（mini-batch gradient descent）每次是挑一个批量计算损失，所以每一次更新参数的时候所使用的损失函数是有差异的。选到第一个批量的时候，用 $L_1$ 计算梯度；选到第二个批量的时候，用 $L_2$ 计算梯度。假设用 $L_1$ 算梯度的时候，梯度是零，就会卡住。但 $L_2$ 的函数跟 $L_1$ 又不一样，$L_2$ 不一定会卡住，可以换下个批量的损失 $L_2$ 计算梯度，模型还是可以训练，还是有办法让损失变小，所以这种有噪声的更新方式反而对训练其实是有帮助的。

其实小的批量也对测试有帮助。假设有一些方法（比如调大的批量的学习率）可以把大的批量跟小的批量训练得一样好。实验结果发现小的批量在测试的时候会是比较好的。在论文“On Large-Batch Training for Deep Learning: Generalization Gap and Sharp Minima”中，作者在不同数据集上训练了六个网络（包括全连接网络、不同的卷积神经网络），在很多不同的情况都观察到一样的结果。在小的批量，一个批量里面有 256 笔样本。在大的批量中，批量大小等于数据集样本数乘 0.1。比如数据集有 60000 笔数据，则一个批量里面有 6000 笔数据。大的批量跟小的批量的训练准确率（accuracy）差不多，但就算是在训练的时候结果差不多，测试的时候，大的批量比小的批量差，代表过拟合。

这篇论文给出了一个解释，如图 3.13 所示，训练损失上面有多个局部最小值，这些局部最小值的损失都很低，其损失可能都趋近于 0。但是局部最小值有好最小值跟坏最小值之分，如果局部最小值在一个“峡谷”里面，它是坏的最小值；如果局部最小值在一个平原上，它是好的最小值。训练的损失跟测试的损失函数是不一样的，这有两种可能。一种可能是本来训练跟测试的分布就不一样；另一种可能是因为训练跟测试都是从采样的数据算出来的，训练跟测试采样到的数据可能不一样，所以它们计算出的损失是有一点差距。 对在一个“盆地”里面的最小值，其在训练跟测试上面的结果不会差太多，只差了一点点。但对在右边在“峡谷”里面的最小值，一差就可以天差地远 。虽然它在训练集上的损失很低，但训练跟测试之间的损失函数不一样，因此测试时，损失函数一变，计算出的损失就变得很大。

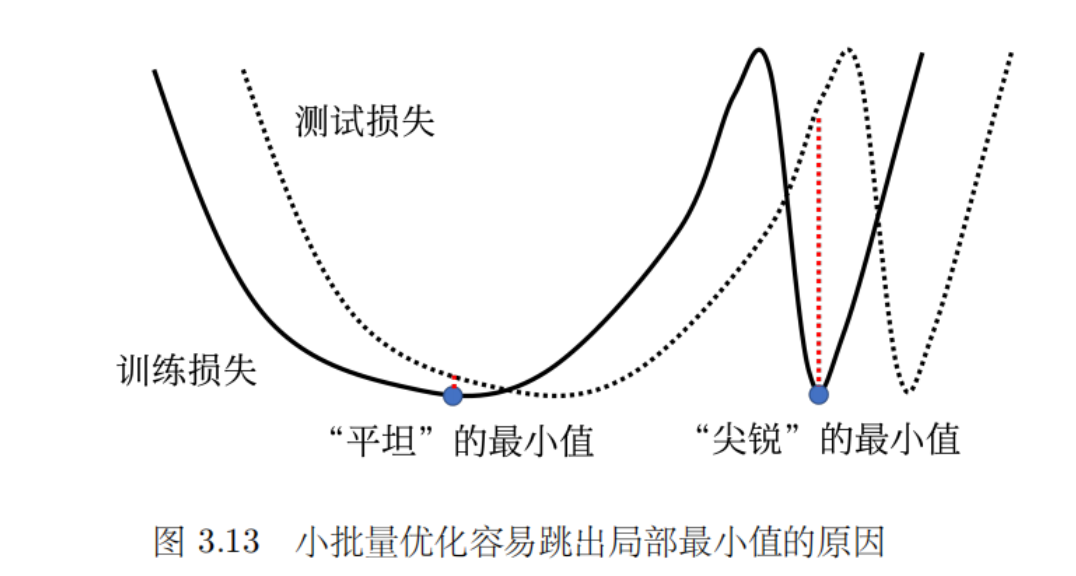
大的批量大小会让我们倾向于走到“峡谷”里面，而小的批量大小倾向于让我们走到“盆地”里面。小的批量有很多的损失，其更新方向比较随机，其每次更新的方向都不太一样。即使“峡谷”非常窄，它也可以跳出去，之后如果有一个非常宽的“盆地”，它才会停下来。

大的批量跟小的批量的对比结果如表 3.1 所示。在有并行计算的情况下，小的批量跟大的批量运算的时间并没有太大的差距。除非大的批量非常大，才会显示出差距。但是一个回合需要的时间，小的批量比较长，大的批量反而是比较快的，所以从一个回合需要的时间来看，大的批量是较有优势的。 而小的批量更新的方向比较有噪声的，大的批量更新的方向比较稳定。但是有噪声的更新方向反而在优化的时候有优势，而且在测试的时候也会有优势。所以大的批量跟小的批量各有优缺点，批量大小是需要去调整的超参数。

其实用大的批量大小来做训练，用并行计算的能力来增加训练的效率，并且训练出的结果很好是可以做到的。比如 76 分钟训练 BERT，15 分钟训练 ResNet，一分钟训练ImageNet等等。这些论文批量大小很大，比如论文“Large Batch Optimization for DeepLearning: Training BERT in 76 minutes ”中批量大小为三万。批量大小很大可以算得很快，这些论文有一些特别的方法来解决批量大小可能会带来的劣势。

动量法

动量法 (momentum method) 是另外一个可以对抗鞍点或局部最小值点的方法。如图3.14所示，假设误差表面就是真正的斜坡，参数是一个球，把球从斜坡上滚下来，如果使用梯度下降，球走到或鞍点就停住了。但是在物理的世界里，一个球如果从高处滚下来，就算滚到鞍点或局部最小值点，因为惯性的关系它还是会继续往前走。如果球的动量足够大，其甚至翻过小坡继续往前走。因此在物理的世界里面，一个球从高处滚下来的时候，它并不一定会被鞍点或局部最小值点卡住，如果将其应用到梯度下降中，这就是动量。

一般的梯度下降 (vanilla gradient descent) 如图3.15所示。初始参数为 ${\theta }_0$，计算一下梯度，计算完梯度后，往梯度的反方向去更新参数 ${\theta }_1={\theta }_0-\eta g_0$。有了新的参数 ${\theta }_1$ 后，再计算一次梯度，再往梯度的反方向，再更新一次参数，到了新的位置以后再计算一次梯度，再往梯度的反方向去更新参数。

引入动量后，每次在移动参数的时候，不是只往梯度的反方向来移动参数，而是根据梯度的反方向加上前一步移动的方向决定移动方向。图3.16中红色虚线方向是梯度的反方向，蓝色虚线方向是前一次更新的方向，蓝色实线的方向是下一步要移动的方向。把前一步指示的方向跟梯度指示的方向相加就是下一步的移动方向。如图3.16所示，初始的参数值为 ${\theta }_0=0$，前一步的参数的更新量为 $m_0=0$。接下来在 ${\theta }_0$ 的地方，计算梯度的方向 $g_0$。下一步的方向是梯度的方向加上前一步的方向，不过因为前一步正好是 0，所以更新的方向跟原来的梯度下降是相同的。但从第二步开始就不太一样了。从第二步开始，计算 $g_1$，接下来更新的方向为 $m_2=\lambda m_1-\eta g_1$，参数更新为 ${\theta }_2$，接下来就反复进行同样的过程。

每一步的移动都用 $m$来表示。$m$其实可以写成之前所有计算的梯度的加权和，如式(3.13)所示。其中 $\eta$ 是学习率，$\lambda$ 是前一个方向的权重参数，也是需要调的。引入动量后，可以从两个角度来理解动量法。一个角度是动量是梯度的反方向加上前一次移动的方向。另外一个角度是当加上动量的时候，更新的方向不是只考虑现在的梯度，而是考虑过去所有梯度的总和。

$$\begin{array}{rl}& m_0=0\\ & m_1=-\eta g_0\\ & m_2=-\lambda \eta g_0-\eta g_1\\ & ⋮\end{array}(3.13)$$

动量的简单例子如图 3.17所示。红色表示负梯度方向，蓝色虚线表示前一步的方向，蓝色实线表示真实的移动量。一开始没有前一次更新的方向，完全按照梯度给指示往右移动参数。负梯度方向跟前一步移动的方向加起来，得到往右走的方向。一般梯度下降走到一个局部最小值点或鞍点时，就被困住了。但有动量还是有办法继续走下去，因为动量不是只看梯度，还看前一步的方向。即使梯度方向往左走，但如果前一步的影响力比梯度要大，球还是有可能继续往右走，甚至翻过一个小丘，也许可以走到更好的局部最小值，这就是动量有可能带来的好处。