weight_decay

权重衰减weight_decay参数从入门到精通 (opens new window)

1 什么是权重衰减(Weight Decay)

Weight Decay是一个正则化技术，作用是抑制模型的过拟合，以此来提高模型的泛化性。

它是通过给损失函数增加模型权重L2范数的惩罚(penalty)来让模型权重不要太大，以此来减小模型的复杂度，从而抑制模型的过拟合 (opens new window)。

看完上面那句话，可能很多人已经蒙圈了，这是在说啥。后面我会逐步进行解释，将会逐步回答以下问题：

什么是正则化？
Weight Decay的减小模型参数的思想
L1范数惩罚项和L2范数惩罚项是什么？
为什么Weight Decay参数是在优化器上，而不是在Loss上。
weight decay的调参技巧

2 什么是正则化？

正则化的目标是减小方差或是说减小数据扰动所造成的影响。我们来看下图来理解一下这句话：

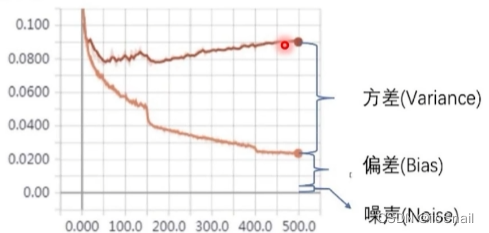
在这里插入图片描述

这幅图是随着训练次数，训练Loss和验证Loss的变化曲线。上面那条线是验证集的。很明显，这个模型出现了过拟合，因为随着训练次数的增加，训练Loss在下降，但是验证Loss却在上升。这里我们会引出三个概念：

方差(Variance)：刻画数据扰动所造成的影响。
偏差(Bias)：刻画学习算法本身的拟合能力。
噪声(Noise)：当前任务任何学习算法能达到的期望泛化误差的下界。也就是数据的噪声导致一定会出现的那部分误差。

通常不考虑噪声，所以偏差和噪声合并称为偏差。

2.1 什么数据扰动

上面说方差是“刻画数据扰动所造成的影响”，我们可以通过下面例子来理解这句话。

假设我们要预测一个 $y = x$ 的模型：

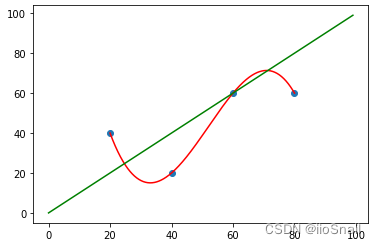
在这里插入图片描述

绿色的线是真正的模型 $y = x$ ，蓝色的点是训练数据，红色的线是预测出的模型。这个训练数据点距离真实模型的偏离程度就是数据扰动。

如果我们使用数据扰动较小的数据，那么预测模型结果就会和真正模型的差距较小，例如：

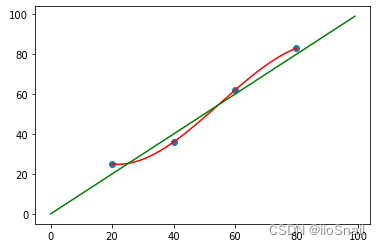
在这里插入图片描述

当我们数据扰动越大，预测模型距离实际模型的差距就会越大。因此，我们减小过拟合就是让预测模型和真实模型尽可能的一致。通常有两种做法：

增加数据量和使用更好的数据。这也是最推荐的做法
然而，通常我们很难收集到更多的数据，所以此时就需要一些正则化技术来减小“数据扰动”对模型预测带来的影响。

3 减小模型权重

权重衰减(Weight Decay)就是减小模型的权重大小，而减小模型的权重大小就可以降低模型的复杂度，使模型变得平滑，进而减小过拟合。

假设我们的模型为： $y = w_{0} + w_{1} x + w_{2} x^{2} + w_{2} x^{2} + \dots + w_{n} x^{n}$ ，模型的参数为 $W = (w_{0}, w_{1}, w_{2}, \dots, w_{n})$

我们使用该模型根据一些训练数据点可能会学到如下的两种曲线：

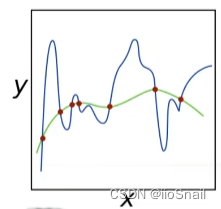
很明显，蓝色的曲线显然过拟合了。如果我们观察 $W$ 的话会发现，蓝色曲线的参数通常都比较大，而绿色曲线的参数通常都比较小。

上面只是直观的说一下。结论就是：模型权重数值越小，模型的复杂度越低。

该结论可以通过实验观察出来，也可以通过数学证明。（李沐说可以证明，感兴趣的同学可以搜一下）

4 为Loss增加惩罚项

上面说了Weight Decay目的是要让模型权重小一点（控制在某一个范围内），以此来减小模型的复杂性，从而抑制过拟合。

而Weight Decay的具体做法就是在Loss后面增加一个权重的L2范数惩罚项。

4.1 通过公式理解Weight Decay

Weight Decay的具体公式就是：

L = L_{0} + \frac{λ}{2} | | W | |^{2}

其中 $L_{0}$ 是原本的Loss， $λ$ 是一个超参，负责控制权重衰减的强弱。 $| | W | |^{2}$ 为模型参数的2范数的平方。

具体的，假设我们的模型有 $n$ 个参数，即 $W = [w_{1}, w_{2}, \dots, w_{n}]$ ，则 $L$ 为：

\begin{aligned} L & = L_{0} + \frac{λ}{2} {(\sqrt{w_{1}^{2} + w_{2}^{2} + \dots + w_{n}^{2}})}^{2} \\ = L_{0} + \frac{λ}{2} (w_{1}^{2} + w_{2}^{2} + \dots + w_{n}^{2}) \end{aligned}

从上面的公式，我们可以很明显的得到如下结论：

模型的权重越大，Loss就会越大。
$λ$ 越大，权重衰减的就越厉害
若 $λ$ 过大，那么原本Loss的占比就会较低，最后模型就光顾着让模型权重变小了，最终模型效果就会变差。

4.2 通过图像理解Weight Decay

接下来我们用图像来感受一下Weight Decay。假设我们的模型只有两个参数W1和W2，W1和W2与Loss=2有如下关系：

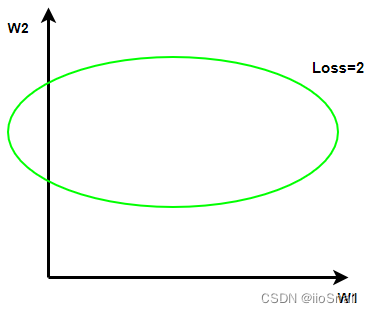
在这里插入图片描述

这个绿色的椭圆表示，当W1和W2取绿色椭圆上的点时，Loss都是2。所以，当我们没有惩罚项时，对于Loss=2，取椭圆上的这些点都可以。若取到右上角的点，那么 W1和W2 的值就会比较大，所以我们希望W1和W2尽量往左下靠。

因为我们的惩罚项是 $w_{1}^{2} + w_{2}^{2}$ ，我们将其图像画出来（ $w_{1}^{2} + w_{2}^{2} = X$ ）。

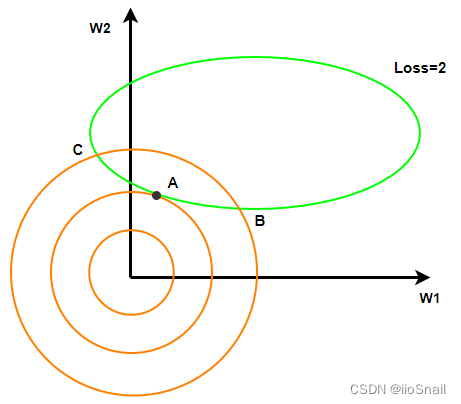
在这里插入图片描述

上图我绘制了三条橘色图像，分别为

$w_{1}^{2} + w_{2}^{2} = X_{1}$ ，与椭圆无焦点。 $w_{1}^{2} + w_{2}^{2} = X_{2}$ ，与椭圆交于A点 $w_{1}^{2} + w_{2}^{2} = X_{3}$ ，与椭圆交于B,C两点

从上图可以看到，在不改变原Loss的情况下，(W1, W2)落在A点时，惩罚项最小，即 $w_{1}^{2} + w_{2}^{2}$ 最小。

所以，我们增加2范数的惩罚，会让模型参数变小。

为什么1范数不好

可能有些同学比较好奇，为什么不取1范数，我们同样用图可以表示出来。我们将上述的2范数图像变成1范数图像（即 $| w_{1} | + | w_{2} | = X$ ）：

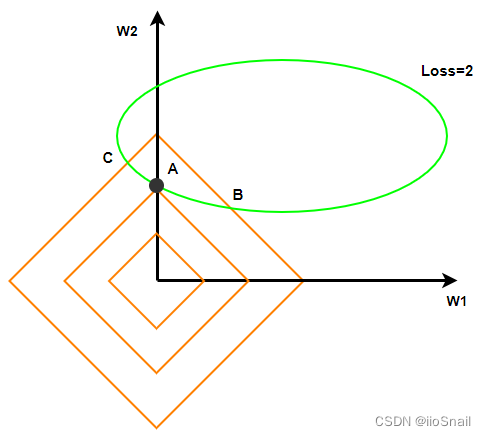
在这里插入图片描述
上图我绘制了三条橘色图像，分别为

$| w_{1} | + | w_{2} | = X_{1}$ ，与椭圆无焦点。
$| w_{1} | + | w_{2} | = X_{2}$ ，与椭圆交于A点
$| w_{1} | + | w_{2} | = X_{3}$ ，与椭圆交于B,C两点

与2范数同理，在不改变原Loss的情况下，(W1, W2)落在A点时，惩罚项最小，即 $| w_{1} | + | w_{2} |$ 最小。

但这里有个问题，我们发现此时 $w_{1}$ 变成 0 了。这就是为什么我们通常不用1范数，因为1范数会倾向于让一部分权重变成0。

更高的范数同理，可以参考“什么是范数（Norm），其具有哪些性质 (opens new window)”这篇博客来感受一下每个范数不同的图像，然后将其套到上面的图中，感受一下其他范数。

5 Weight Decay的实现

通常我们在使用Weight Decay是在优化器(Optimizer)上，这就很奇怪了，上面明明都是在说Loss，为什么weight decay参数是在优化器上呢？

这是因为它们是等价的。这个很容易推导，我们用SGD来举例，SGD的更新参数的过程为：

w_{i} - γ \frac{\partial L}{\partial w_{i}}

其中 $γ$ 是学习率。

我们将 $L = L_{0} + \frac{λ}{2} | | W | |^{2}$ 带进来求一下可得：

\begin{aligned} w_{i} - γ \frac{\partial L}{\partial w_{i}} \\ = & w_{i} - γ (\frac{\partial L_{0}}{\partial w_{i}} + λ w_{i}) \end{aligned}

其中 $\frac{\partial L_{0}}{\partial w_{i}}$ 就是原本的梯度，所以我们为Loss增加L2正则项只需要在更新参数时，给模型的梯度加一个 $λ w_{i}$ 即可。

对应Pytorch的实现如下图：

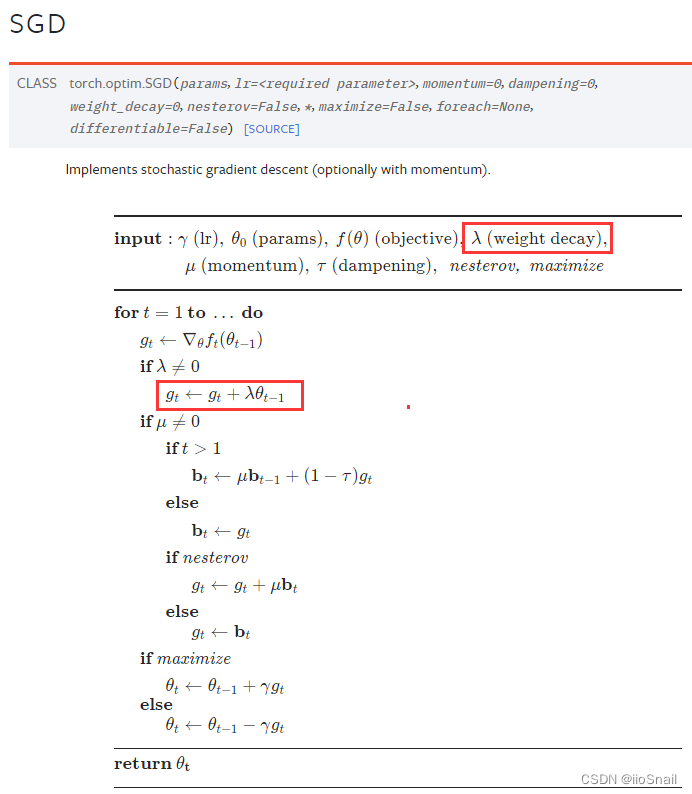
在这里插入图片描述

6 weight_decay的一些trick

weight_decay并没有你想想中的那么好，它的效果可能只有一点点，不要太指望它。尤其是当你的模型很复杂时，权重衰退的效果可能会更小了。
通常取1e-3，如果要尝试的话，一般也就是1e-2, 1e-3, 1e-4 这些选项。
权重衰退通常不对bias做。但通常bias做不做权重衰退其实效果差不多，不过最好不要做。
weight_decay取值越大，对抑制模型的强度越大。但这并不说明越大越好，太大的话，可能会导致模型欠拟合。

针对第三点：对于一个二维曲线，bias只是让曲线整体上下移动，并不能减小模型的复杂度，所以通常不需要对bias做正则化。

参考资料

正则化之weight_decay(深度之眼) (opens new window): https://www.bilibili.com/video/BV1HB4y1i7Fn

权重衰退(李沐) (opens new window): https://www.bilibili.com/video/BV1UK4y1o7dy

从拉格朗日乘数法角度理解L1L2正则 (opens new window): https://www.bilibili.com/video/BV1Z44y147xA

上次更新: 2025/07/06, 13:25:25

← 学习率优化器→