归一化、标准化和正则化

归一化 Normalization

归一化一般是将数据映射到指定的范围，用于去除不同维度数据的量纲以及量纲单位。

常见的映射范围有 [0, 1] 和 [-1, 1] ，最常见的归一化方法就是 Min-Max 归一化：

Min-Max 归一化

x_{n e w} = \frac{x - x_{m i n}}{x_{m a x} - x_{m i n}}

举个例子，我们判断一个人的身体状况是否健康，那么我们会采集人体的很多指标，比如说：身高、体重、红细胞数量、白细胞数量等。

一个人身高 180cm，体重 70kg，白细胞计数 $7.50 \times 10^{9} / L$ ，etc.

衡量两个人的状况时，白细胞计数就会起到主导作用从而遮盖住其他的特征，归一化后就不会有这样的问题。

标准化 Normalization

归一化和标准化的英文翻译是一致的，但是根据其用途（或公式）的不同去理解（或翻译）

下面我们将探讨最常见的标准化方法： Z-Score 标准化。

Z-Score 标准化

x_{n e w} = \frac{x - μ}{σ}

其中 $μ$ 是样本数据的均值（mean）， $σ$ 是样本数据的标准差（std）。

上图则是一个散点序列的标准化过程：原图->减去均值->除以标准差。

显而易见，变成了一个均值为 0 ，方差为 1 的分布，下图通过 Cost 函数让我们更好的理解标准化的作用。

机器学习的目标无非就是不断优化损失函数，使其值最小。在上图中， $J (w, b)$ 就是我们要优化的目标函数

我们不难看出，标准化后可以更加容易地得出最优参数 $w$ 和 $b$ 以及计算出 $J (w, b)$ 的最小值，从而达到加速收敛的效果。 $^{[1]}$

注：上图来源于 Andrew Ng 的课程讲义

Batch Normalization

BatchNorm是对一个batch-size样本内的每个特征[分别]做归一化，LayerNorm是[分别]对每个样本的所有特征做归一化

在机器学习中，最常用标准化的地方莫过于神经网络的 BN 层（Batch Normalization），因此我们简单的谈谈 BN 层的原理和作用，想要更深入的了解可以https://arxiv.org/abs/1502.03167 (opens new window)。

我们知道数据预处理做标准化可以加速收敛，同理，在神经网络使用标准化也可以加速收敛，而且还有如下好处：

具有正则化的效果（Batch Normalization reglarizes the model）
提高模型的泛化能力（Be advantageous to the generalization of network）
允许更高的学习速率从而加速收敛（Batch Normalization enables higher learning rates）

其原理是利用正则化减少内部相关变量分布的偏移（Reducing Internal Covariate Shift），从而提高了算法的鲁棒性。 $^{[2]}$

BN 效果

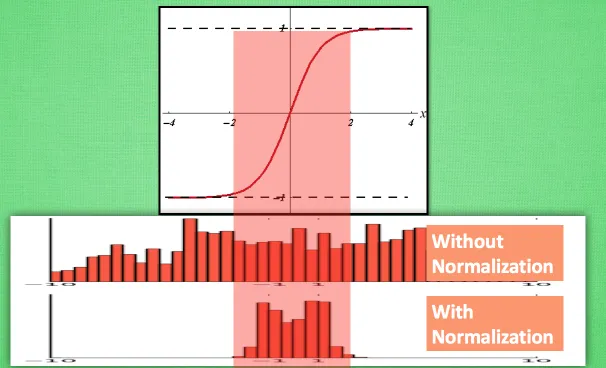
Batch normalization 可以被看做一个层面. 在一层层的添加神经网络的时候, 我们先有数据 $X$ , 再添加全连接层, 全连接层的计算结果会经过激励函数成为下一层的输入, 接着重复之前的操作. Batch Normalization (BN) 就被添加在每一个全连接和激励函数之间.

之前说过, 计算结果在进入激励函数前的值很重要, 如果我们不单单看一个值, 我们可以说, 计算结果值的分布对于激励函数很重要。对比这两个在激活之前的值的分布. 上者没有进行 normalization, 下者进行了 normalization, 这样当然是下者能够更有效地利用 tanh 进行非线性化的过程.

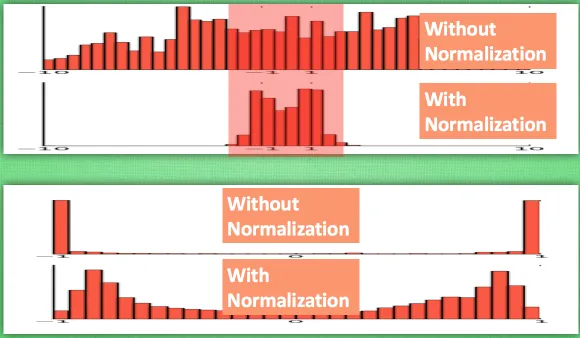
没有 normalize 的数据使用 tanh 激活以后, 激活值大部分都分布到了饱和阶段, 也就是大部分的激活值不是-1, 就是1, 而 normalize 以后, 大部分的激活值在每个分布区间都还有存在. 再将这个激活后的分布传递到下一层神经网络进行后续计算, 每个区间都有分布的这一种对于神经网络就会更加有价值. Batch normalization 不仅仅 normalize 了一下数据, 他还进行了反 normalize 的手续. 为什么要这样呢?

Batch Normalization 由两部分组成，第一部分是缩放与平移（scale and shift），第二部分是训练缩放尺度和平移的参数（train a BN Network），算法步骤如下：

我们引入一些 batch normalization 的公式. 这三步就是我们在刚刚一直说的 normalization 工序, 但是公式的后面还有一个反向操作, 将 normalize 后的数据再扩展和平移. 原来这是为了让神经网络自己去学着使用和修改这个扩展参数 gamma, 和平移参数 β, 这样神经网络就能自己慢慢琢磨出前面的 normalization 操作到底有没有起到优化的作用, 如果没有起到作用, 我就使用 gamma 和 belt 来抵消一些 normalization 的操作。接下来训练 BN 层参数 $γ$ 和 $\beta $ ，限于篇幅的原因按下不表，有兴趣的读者可以拜读https://arxiv.org/abs/1502.03167 (opens new window)。

最后我们来看看一张神经网络训练到最后, 代表了每层输出值的结果的分布图. 这样我们就能一眼看出 Batch normalization 的功效啦. 让每一层的值在有效的范围内传递下去。

正则化 Regularization

正则化主要用于避免过拟合的产生和减少网络误差。

正则化一般具有如下形式：

J (w, b) = \frac{1}{m} \sum_{i = 1}^{m} L (f (x), y) + λ R (f)

其中，第 1 项是经验风险，第 2 项是正则项， $λ \geq 0$ 为调整两者之间关系的系数。

第 1 项的经验风险较小的模型可能较复杂（有多个非零参数），这时第 2 项的模型复杂度会较大。

正则化的作用是选择经验风险与模型复杂度同时较小的模型。 $^{[3]}$

常见的有正则项有 L1 正则 和 L2 正则 以及 Dropout ，其中 L2 正则 的控制过拟合的效果比 L1 正则 的好。

Lp范数

为什么叫 L1 正则，有 L1、L2 正则那么有没有 L3、L4 之类的呢？

首先我们补一补课， $L_{p}$ 正则的 $L$ 是指 $L_{p}$ 范数，其定义为：

$L_{0}$ 范数： ${‖ w ‖}_{0} = # (i) w i t h x_{i} \neq 0$ （非零元素的个数）

$L_{1}$ 范数： ${‖ w ‖}_{1} = \sum_{i = 1}^{d} | x_{i} |$ （每个元素绝对值之和）

$L_{2}$ 范数： ${‖ w ‖}_{2} = (\sum_{i = 1}^{d} x_{i}^{2})^{1 / 2}$ （欧氏距离）

$L_{p}$ 范数： ${‖ w ‖}_{p} = (\sum_{i = 1}^{d} x_{i}^{p})^{1 / p}$

在机器学习中，若使用了 $‖ w ‖_{p}$ 作为正则项，我们则说该机器学习任务引入了 $L_{p}$ 正则项。

上图来自周志华老师的《机器学习》插图

L1 正则 Lasso regularizer

J (w, b) = \frac{1}{m} \sum_{i = 1}^{m} L (\hat{y}, y) + \frac{λ}{m} {‖ w ‖}_{1} ​

凸函数，不是处处可微分
得到的是稀疏解（最优解常出现在顶点上，且顶点上的 $w$ 只有很少的元素是非零的）

L2 正则 Ridge Regularizer / Weight Decay

J (w, b) = \frac{1}{m} \sum_{i = 1}^{m} L (\hat{y}, y) + \frac{λ}{2 m} {‖ w ‖}_{2}^{2} ​

凸函数，处处可微分
易于优化

Dropout

Dropout 主要用于神经网络，其原理是使神经网络中的某些神经元随机失活，让模型不过度依赖某一神经元，达到增强模型鲁棒性以及控制过拟合的效果。

除此之外，Dropout 还有多模型投票等功能，若有兴趣可以拜读https://www.cs.toronto.edu/~hinton/absps/JMLRdropout.pdf (opens new window)。

Reference

[1] LeCun, Y., Bottou, L., Orr, G., and Muller, K. Efficient backprop. In Orr, G. and K., Muller (eds.), Neural Net-works: Tricks of the trade. Springer, 1998b.

[2] Sergey Ioffe, Christian Szegedy, “Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift”, arXiv preprint arXiv:1502.03167, 2015.

[3] 李航. 统计方法学 P13-14

[4] 聊聊机器学习中的损失函数 [http://kubicode.me/2016/04/11/Machine Learning/Say-About-Loss-Function/](http://kubicode.me/2016/04/11/Machine Learning/Say-About-Loss-Function/)

[5] Nitish Srivastava, Geoffrey Hinton, Alex Krizhevsky, Ilya Sutskever and Ruslan Salakhutdinov, "Dropout: A Simple Way to Prevent Neural Networks from
Overfitting",

[6] ML 入门：归一化、标准化和正则化 (opens new window)

上次更新: 2025/06/25, 11:25:50

← 单变量线性回归经典网络→