集成学习

集成学习概述

集成学习(ensemble learning)本身不是一个单独的机器学习算法，而是通过构建并结合多个机器学习器来完成学习任务。也就是我们常说的“博采众长”。集成学习可以用于分类问题集成，回归问题集成，特征选取集成，异常点检测集成等等，可以说所有的机器学习领域都可以看到集成学习的身影。

从下图，我们可以对集成学习的思想做一个概括。对于训练集数据，我们通过训练若干个个体学习器（individual learner），通过一定的结合策略，就可以最终形成一个强学习器，以达到博采众长的目的。

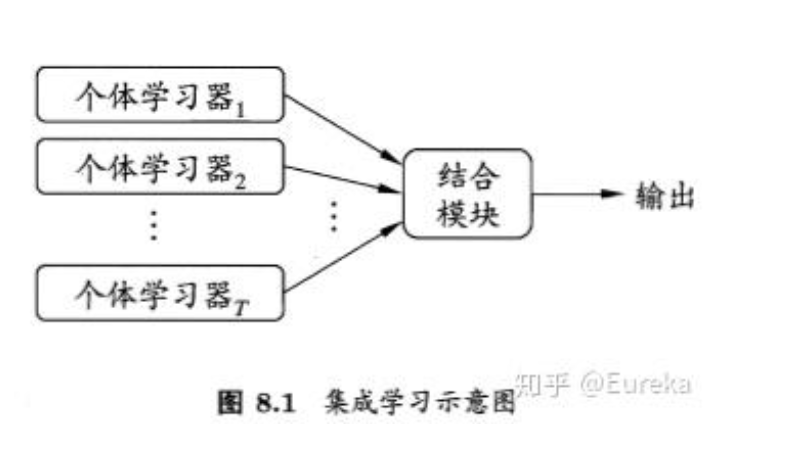
也就是说，集成学习有两个主要的问题需要解决，第一是如何得到若干个个体学习器，第二是如何选择一种结合策略，将这些个体学习器集合成一个强学习器。

集成学习之个体学习器

集成学习的第一个问题就是如何得到若干个个体学习器。这里有两种选择。第一种就是所有的个体学习器都是一个种类的，或者说是同质的（homogeneous），同质集成中的个体学习器也称为“基学习器”（base learner），相应的学习算法称为“基学习算法”（base learning algorithm）。比如都是决策树个体学习器，或者都是神经网络个体学习器。第二种是所有的个体学习器不全是一个种类的，或者说是异质的（heterogeneous）。比如我们有一个分类问题，对训练集采用支持向量机个体学习器，逻辑回归个体学习器和朴素贝叶斯个体学习器来学习，再通过某种结合策略来确定最终的分类强学习器。这时个体学习器一般不称为基学习器，而称作“组件学习器”（component leaner）或直接称为个体学习器。

弱学习器（weak learner）：指泛化性能略优于随机猜测的学习器：例如在二分类问题桑精度略高于50%的分类器。

前面提到，集成学习的直觉是结合多个个体的能力，获得远超个体的集体能力优势。这种直觉在实际上对于“弱学习器”是非常符合的。故很多集成学习的研究也都是针对弱学习器，而基学习器有时也被直接称为弱学习器。

一般经验中，如果把好坏不一的东西掺杂在一起，那么最终结果很可能是整体效果比最坏的东西要好一些，但又比最好的那个要坏一些，那么这种情况下不如就让最好的单独去工作，而不要参与混合。但是集成学习还是对多个学习器进行了结合，那它怎么保证整体的效果会比最好的那个单一学习器的效果更好呢。

用一个简单的例子来进行说明：在一个二分类任务中，假设三个分类器在三个测试样本上的表现如下图所示。假设集成学习的结果通过三个个体学习器用投票发（voting）产生，即“少数服从多数”，那么当三个个体学习器分别对三个测试例有不同的判别优势时，集成的效果也会不一样。

在（a）中，每个分类器原本只有66.6%的精度，集成学习却达到了100%；（b）中，每个分类器都是一样的，集成之后性能没有任何提高；在（c）中，每个分类器的精度只有33.3%，集成之后结果反而变得更糟。

这个例子表明：要获得好的集成，个体学习器应“好而不同”，即个体学习器要有一定的准确性，即学习器不能太坏，并且要有“多样性”（diversity），即学习器间具有差异。

根据个体学习器生成方式的不同，目前集成学习方法大致可分为两大类，第一个是个体学习器之间存在强依赖关系，一系列个体学习器基本都需要串行生成的序列化方法，代表算法是boosting系列算法，第二个是个体学习器之间不存在强依赖关系，一系列个体学习器可以并行生成，代表算法是bagging和随机森林（Random Forest）系列算法。

集成学习之boosting

Boosting 训练过程为阶梯状，基模型的训练是有顺序的，每个基模型都会在前一个基模型学习的基础上进行学习，最终综合所有基模型的预测值产生最终的预测结果，用的比较多的综合方式为加权法。

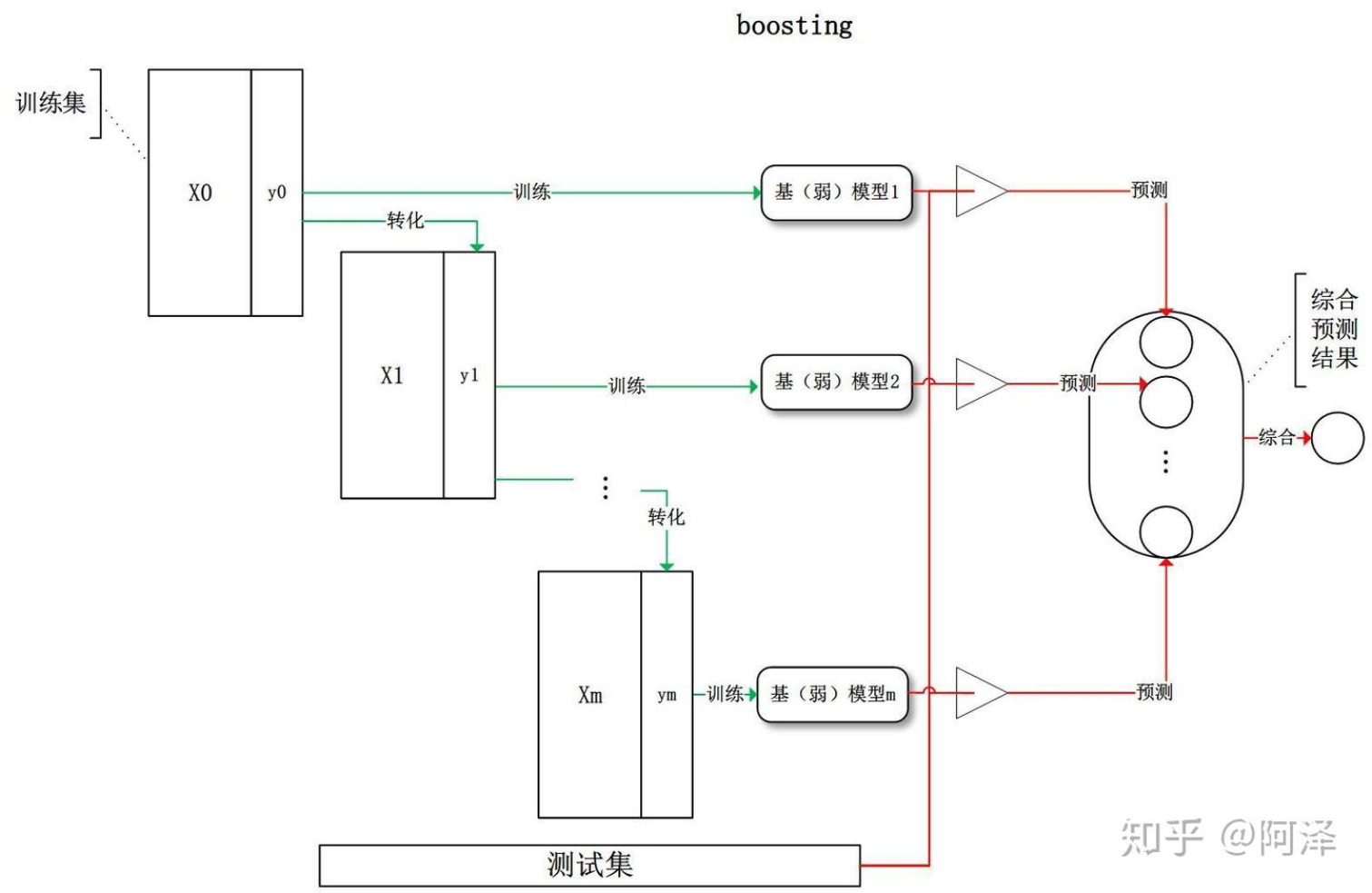
Boosting算法的工作机制是首先从训练集用初始权重训练出一个弱学习器1，根据弱学习的学习误差率表现来更新训练样本的权重，使得之前弱学习器1学习误差率高的训练样本点的权重变高，使得这些误差率高的点在后面的弱学习器2中得到更多的重视。然后基于调整权重后的训练集来训练弱学习器2.，如此重复进行，直到弱学习器数达到事先指定的数目T，最终将这T个弱学习器通过集合策略进行整合，得到最终的强学习器。

Boosting系列算法里最著名算法主要有AdaBoost算法和提升树(boosting tree)系列算法。提升树系列算法里面应用最广泛的是梯度提升树(Gradient Boosting Tree)。

集成学习之bagging

Bagging 全称叫 Bootstrap aggregating ，每个基学习器都会对训练集进行有放回抽样得到子训练集，比较著名的采样法为 0.632 自助法。每个基学习器基于不同子训练集进行训练，并综合所有基学习器的预测值得到最终的预测结果。Bagging 常用的综合方法是投票法，票数最多的类别为预测类别。

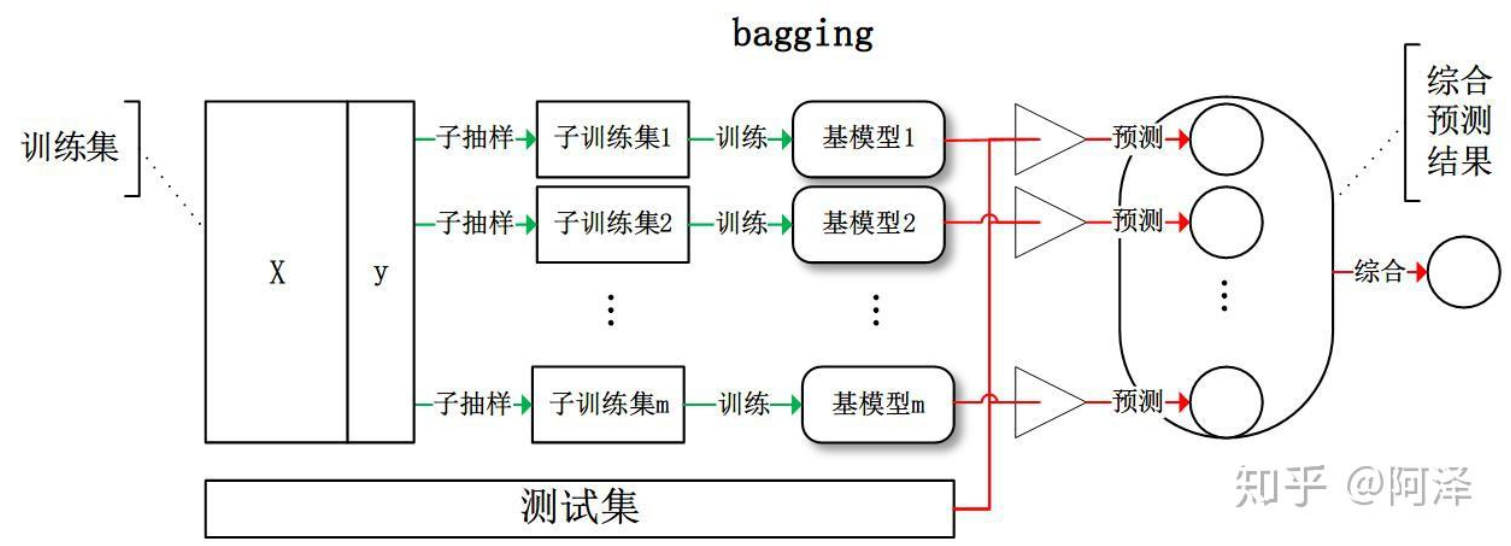
对于这里的随机采样有必要做进一步的介绍，这里一般采用的是自助采样法（Bootstap sampling）,即对于 $m$ 个样本的原始训练集，我们每次先随机采集一个样本放入采样集，接着把该样本放回，也就是说下次采样时该样本仍有可能被采集到，这样采集 $m$ 次，最终可以得到 $m$ 个样本的采样集，由于是随机采样，这样每次的采样集是和原始训练集不同的，和其他采样集也是不同的，这样得到多个不同的弱学习器。

注：Bootstrap方法是非常有用的一种统计学上的估计方法。 Bootstrap是一类非参Monte Carlo方法,其实质是对观测信息进行再抽样，进而对总体的分布特性进行统计推断。首先，Bootstrap通过重抽样，避免了Cross-Validation造成的样本减少问题，其次，Bootstrap也可以创造数据的随机性。Bootstrap是一种有放回的重复抽样方法，抽样策略就是简单的随机抽样。

随机森林（Random Forest，简称RF）是Bagging的一个扩展变体。其在以决策树作为基学习器构建Bagging集成的基础上，进一步在决策树的训练过程中引入了随机属性选择。

具体来说，传统决策树在选择划分属性时是在当前结点的属性集合（假定有 $d$ 个属性）中选择一个最优属性；而在RF中，对基决策树的每个结点，先从该结点的属性集合中随机选择一个包含 $k$ 个属性的子集，然后再从这个子集中选择一个最优属性用于划分。这里的参数 $k$ 控制了随机性的引入程度：若令 $k = d$ ，则基决策树的构建与传统决策树相同；若令 $k = 1$ ，则是随机选择一个属性用于划分；一般情况下，推荐值 $k = l o g_{2} d$ 。

集成学习之Stacking

Stacking 是先用全部数据训练好基模型，然后每个基模型都对每个训练样本进行的预测，其预测值将作为训练样本的特征值，最终会得到新的训练样本，然后基于新的训练样本进行训练得到模型，然后得到最终预测结果。

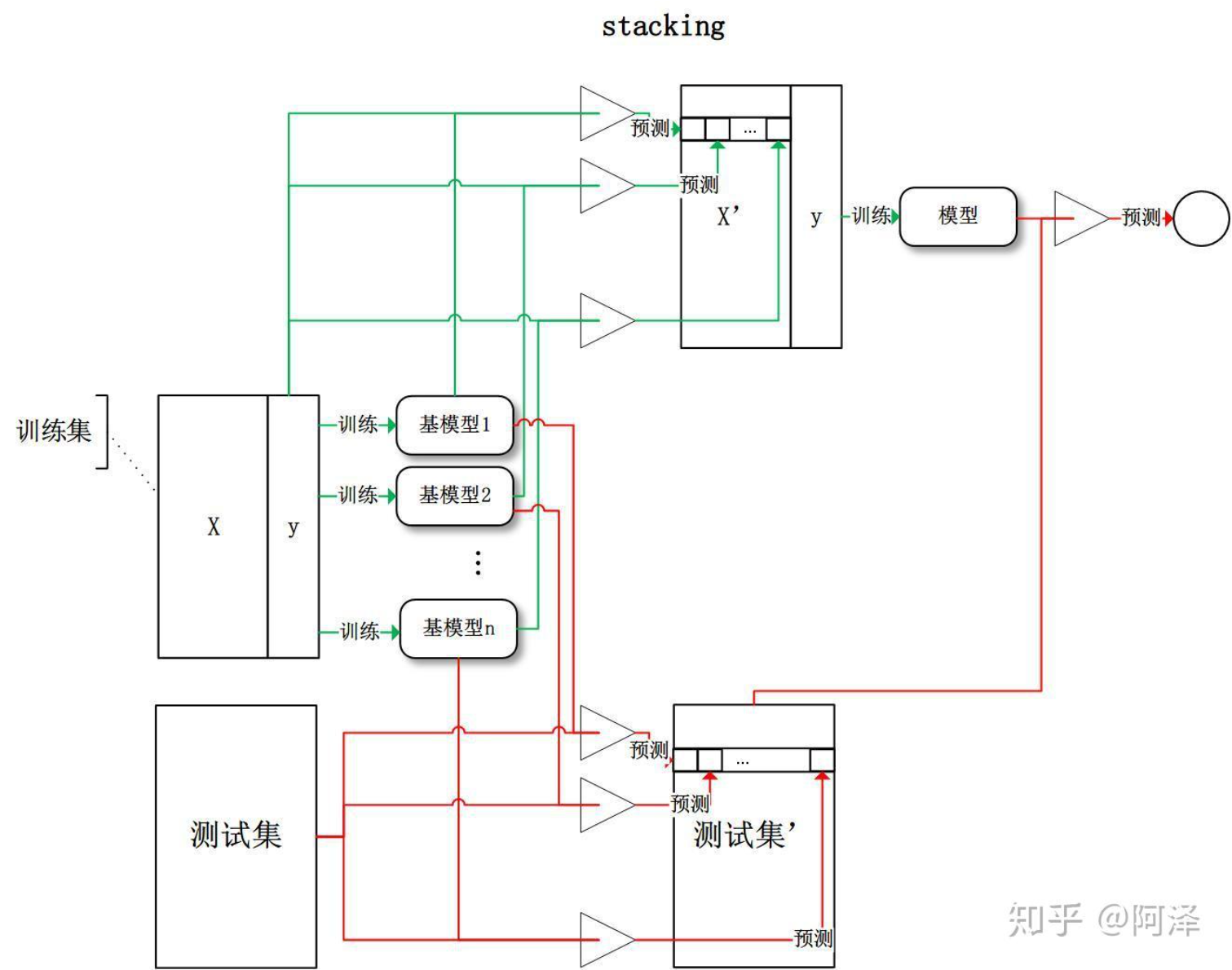
Stacking算法分为2层，第一层是用不同的算法形成 $T$ 弱分类器，同时产生一个与原数据集大小相同的新数据集，利用这个新数据集和一个新算法构成第二层的分类器。

Stacking 就像是 Bagging的升级版，Bagging中的融合各个基础分类器是相同权重，而Stacking中则不同,Stacking中第二层学习的过程就是为了寻找合适的权重或者合适的组合方式。

那么，为什么集成学习会好于单个学习器呢？原因可能有三：

训练样本可能无法选择出最好的单个学习器，由于没法选择出最好的学习器，所以干脆结合起来一起用；
假设能找到最好的学习器，但由于算法运算的限制无法找到最优解，只能找到次优解，采用集成学习可以弥补算法的不足；
可能算法无法得到最优解，而集成学习能够得到近似解。比如说最优解是一条对角线，而单个决策树得到的结果只能是平行于坐标轴的，但是集成学习可以去拟合这条对角线。

偏差与方差角度的集成学习

集成学习的偏差与方差

偏差（Bias）描述的是预测值和真实值之差；方差（Variance）描述的是预测值作为随机变量的离散程度。放一场很经典的图：

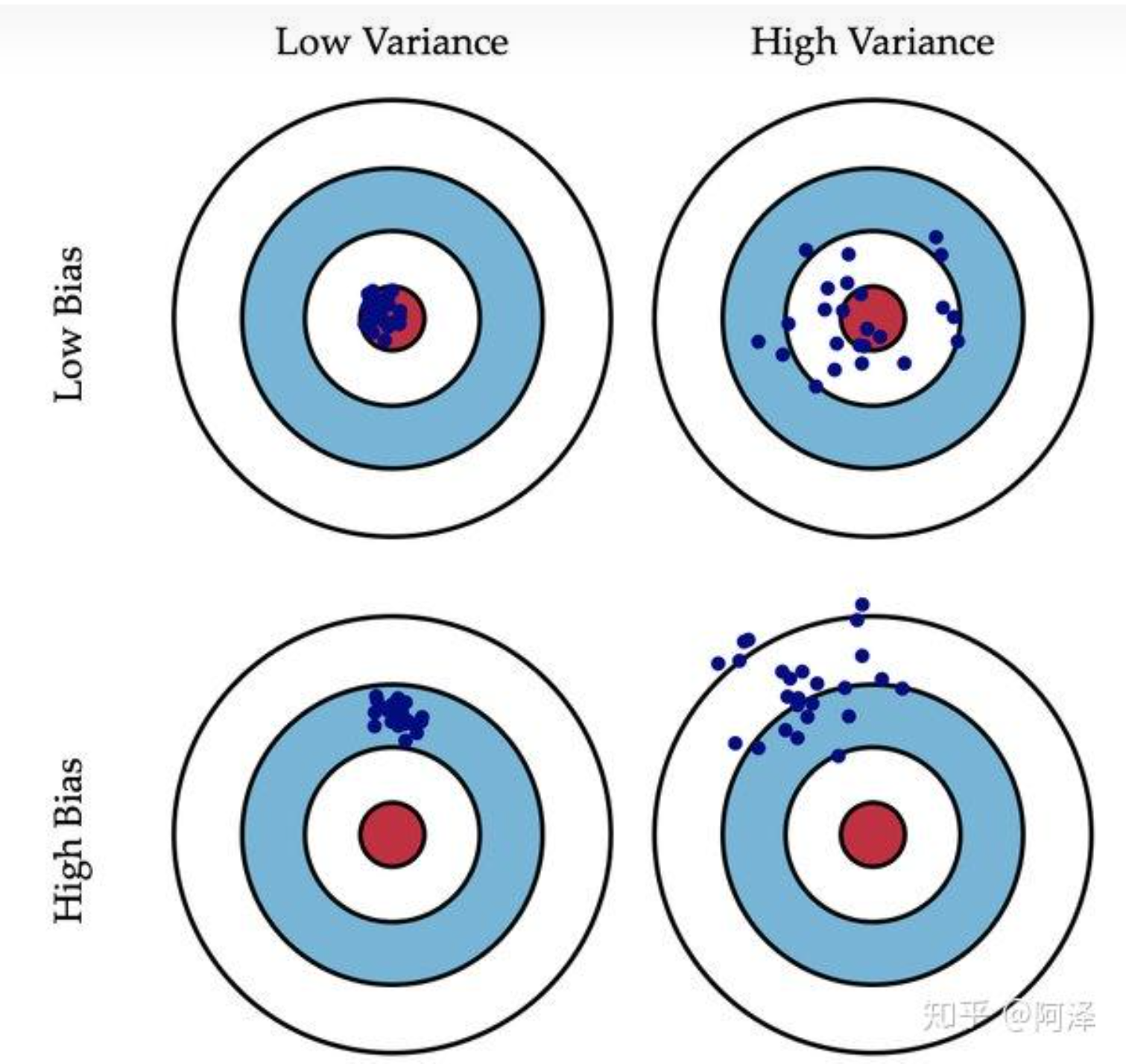
模型的偏差与方差

**偏差：**描述样本拟合出的模型的预测结果的期望与样本真实结果的差距，要想偏差表现的好，就需要复杂化模型，增加模型的参数，但这样容易过拟合，过拟合对应上图的 High Variance，点会很分散。低偏差对应的点都打在靶心附近，所以喵的很准，但不一定很稳；
**方差：**描述样本上训练出来的模型在测试集上的表现，要想方差表现的好，需要简化模型，减少模型的复杂度，但这样容易欠拟合，欠拟合对应上图 High Bias，点偏离中心。低方差对应就是点都打的很集中，但不一定是靶心附近，手很稳，但不一定瞄的准。

我们常说集成学习中的基模型是弱模型，通常来说弱模型是偏差高（在训练集上准确度低）方差小（防止过拟合能力强）的模型，但并不是所有集成学习框架中的基模型都是弱模型。Bagging 和 Stacking 中的基模型为强模型（偏差低，方差高），而Boosting 中的基模型为弱模型（偏差高，方差低）。

在 Bagging 和 Boosting 框架中，通过计算基模型的期望和方差我们可以得到模型整体的期望和方差。为了简化模型，我们假设基模型的期望为 $μ$ ，方差 $σ^{2}$ ，模型的权重为 $r$ ，两两模型间的相关系数 $ρ$ 相等。由于 Bagging 和 Boosting 的基模型都是线性组成的，那么有：

模型总体期望：

\begin{aligned} E (F) & = E (\sum_{i}^{m} r_{i} f_{i}) \\ = \sum_{i}^{m} r_{i} E (f_{i}) \end{aligned}

模型总体方差（公式推导参考协方差的性质，协方差与方差的关系）：

\begin{aligned} V a r (F) & = V a r (\sum_{i}^{m} r_{i} f_{i}) \\ = \sum_{i}^{m} V a r (r_{i} f_{i}) + \sum_{i \neq j}^{m} C o v (r_{i} f_{i}, r_{j} f_{j}) \\ = \sum_{i}^{m} {r_{i}}^{2} V a r (f_{i}) + \sum_{i \neq j}^{m} ρ r_{i} r_{j} \sqrt{V a r (f_{i})} \sqrt{V a r (f_{j})} \\ = m r^{2} σ^{2} + m (m - 1) ρ r^{2} σ^{2} \\ = m r^{2} σ^{2} (1 - ρ) + m^{2} r^{2} σ^{2} ρ \end{aligned}

模型的准确度可由偏差和方差共同决定：

E r r o r = b i a s^{2} + v a r + ξ

Bagging 的偏差与方差

对于 Bagging 来说，每个基模型的权重等于 1/m 且期望近似相等，故我们可以得到：

\begin{aligned} E (F) & = \sum_{i}^{m} r_{i} E (f_{i}) \\ = m \frac{1}{m} μ \\ = μ \\ V a r (F) & = m r^{2} σ^{2} (1 - ρ) + m^{2} r^{2} σ^{2} ρ \\ = m \frac{1}{m^{2}} σ^{2} (1 - ρ) + m^{2} \frac{1}{m^{2}} σ^{2} ρ \\ = \frac{σ^{2} (1 - ρ)}{m} + σ^{2} ρ \end{aligned}

通过上式我们可以看到：

整体模型的期望等于基模型的期望，这也就意味着整体模型的偏差和基模型的偏差近似。
**整体模型的方差小于等于基模型的方差，当且仅当相关性为 1 时取等号，随着基模型数量增多，整体模型的方差减少，从而防止过拟合的能力增强，模型的准确度得到提高。**但是，模型的准确度一定会无限逼近于 1 吗？并不一定，当基模型数增加到一定程度时，方差公式第一项的改变对整体方差的作用很小，防止过拟合的能力达到极限，这便是准确度的极限了。

在此我们知道了为什么 Bagging 中的基模型一定要为强模型，如果 Bagging 使用弱模型则会导致整体模型的偏差提高，而准确度降低。

Random Forest 是经典的基于 Bagging 框架的模型，并在此基础上通过引入特征采样和样本采样来降低基模型间的相关性，在公式中显著降低方差公式中的第二项，略微升高第一项，从而使得整体降低模型整体方差。

Boosting 的偏差与方差

对于 Boosting 来说，由于基模型共用同一套训练集，所以基模型间具有强相关性，故模型间的相关系数近似等于 1，针对 Boosting 化简公式为：

\begin{aligned} E (F) & = \sum_{i}^{m} r_{i} E (f_{i}) \\ V a r (F) & = m r^{2} σ^{2} (1 - ρ) + m^{2} r^{2} σ^{2} ρ \\ = m \frac{1}{m^{2}} σ^{2} (1 - 1) + m^{2} \frac{1}{m^{2}} σ^{2} 1 \\ = σ^{2} \end{aligned}

通过观察整体方差的表达式我们容易发现：

整体模型的方差等于基模型的方差，如果基模型不是弱模型，其方差相对较大，这将导致整体模型的方差很大，即无法达到防止过拟合的效果。因此，Boosting 框架中的基模型必须为弱模型。
此外 Boosting 框架中采用基于贪心策略的前向加法，整体模型的期望由基模型的期望累加而成，所以随着基模型数的增多，整体模型的期望值增加，整体模型的准确度提高。

基于 Boosting 框架的 Gradient Boosting Decision Tree 模型中基模型也为树模型，同 Random Forrest，我们也可以对特征进行随机抽样来使基模型间的相关性降低，从而达到减少方差的效果。

小结

我们可以使用模型的偏差和方差来近似描述模型的准确度；
对于 Bagging 来说，整体模型的偏差与基模型近似，而随着模型的增加可以降低整体模型的方差，故其基模型需要为强模型；
对于 Boosting 来说，整体模型的方差近似等于基模型的方差，而整体模型的偏差由基模型累加而成，故基模型需要为弱模型。

️那么这里有一个小小的疑问，Bagging 和 Boosting 到底用的是什么模型呢？

Bagging与Boosting对比

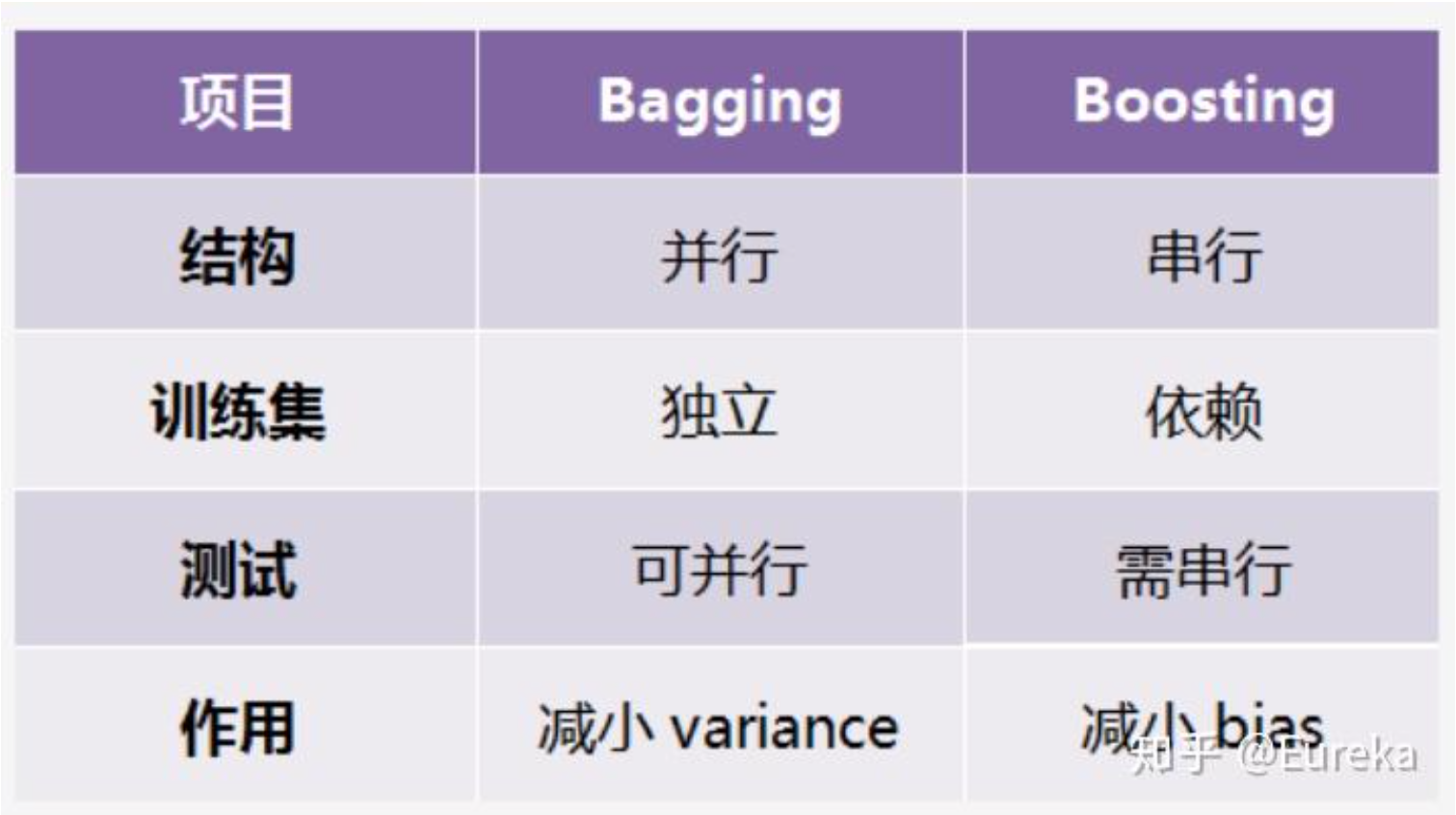
为什么bagging是减少variance，而boosting是减少bias?

为什么说bagging是减少variance，而boosting是减少bias? (opens new window)

Bagging对样本重采样，对每一重采样得到的子样本集训练一个模型，最后取平均。由于子样本集的相似性以及使用的是同种模型，因此各模型有近似相等的bias和variance（事实上，各模型的分布也近似相同，但不独立）。由于 $E [\frac{\sum X_{i}}{n}] = E [X_{i}]$ ，所以bagging后的bias和单个子模型的接近，一般来说不能显著降低bias。另一方面，若各子模型独立，则有 $V a r (\frac{\sum X_{i}}{n}) = \frac{V a r (X_{i})}{n}$ ，此时可以显著降低variance。若各子模型完全相同，则 $V a r (\frac{\sum X_{i}}{n}) = V a r (X_{i})$ ，此时不会降低variance。bagging方法得到的各子模型是有一定相关性的，属于上面两个极端状况的中间态，因此可以一定程度降低variance。为了进一步降低variance，Random forest通过随机选取变量子集做拟合的方式de-correlated了各子模型（树），使得variance进一步降低。

boosting从优化角度来看，是用forward-stagewise这种贪心法去最小化损失函数 $L (y_{i}, \sum_{i} a_{i} f_{i} (x))$ 。例如，常见的AdaBoost即等价于用这种方法最小化exponential loss： $L (y, f (x)) = e x p (- y f (x))$ 。所谓forward-stagewise，就是在迭代的第 $n$ 步，求解新的子模型 $f (x)$ 及步长 $a$ （或者叫组合系数），来最小化 $L (y, f_{n - 1} (x) + α f (x))$ ，这里 $f_{n - 1} (x)$ 是前 $n - 1$ 步得到的子模型的和。因此boosting是在sequential地最小化损失函数，其bias自然逐步下降。但由于是采取这种sequential、adaptive的策略，各子模型之间是强相关的，于是子模型之和并不能显著降低variance。所以说boosting主要还是靠降低bias来提升预测精度。

集成学习之结合策略

假设集成中包含 $T$ 个基学习器 $h_{1}, h_{2}, . . ., h_{T}$ ，其中 $h_{i}$ 在示例 $x$ 上的输出为 $h_{i} (x)$ 。那么对 $h_{i}$ 进行结合的常见策略有以下几种：

6.1 平均法

对于数值类的回归预测问题，通常使用的结合策略是平均法，也就是说，对于若干个弱学习器的输出进行平均得到最终的预测输出。

最简单的平均是算术平均，也就是说最终预测是:

H (x) = \frac{1}{T} \sum_{1}^{T} h_{i} (x)

如果每个个体学习器有一个权重 $w$ ，则最终预测是:

H (x) = \sum_{1}^{T} w_{i} h_{i} (x)

其中 $w_{i}$ 是个体学习器 $h_{i}$ 的权重， $w_{i} \geq 0, \sum_{1}^{T} w_{i} = 1$

一般而言，在个体学习器的性能相差较大时宜使用加权平均法，而在个体学习器性能相近时宜使用简单平均法。

6.2 投票法

对于分类问题的预测，我们通常使用的是投票法。假设我们的预测类别是 ${c_{1}, c_{2}, . . ., c_{K}}$ ，对于任意一个预测样本 $x$ ，我们的 $T$ 个弱学习器的预测结果分别是 $(h_{1} (x), h_{2} (x), . . ., h_{T} (x))$ 。

最简单的投票法是相对多数投票法（plurality voting），也就是我们常说的少数服从多数，也就是 $T$ 个弱学习器的对样本 $x$ 的预测结果中，数量最多的类别 $c_{i}$ 为最终的分类类别。如果不止一个类别获得最高票，则随机选择一个做最终类别。

稍微复杂的投票法是绝对多数投票法（majority voting），也就是我们常说的要票过半数。在相对多数投票法的基础上，不光要求获得最高票，还要求票过半数。否则会拒绝预测。

更加复杂的是加权投票法（weighted voting），和加权平均法一样，每个弱学习器的分类票数要乘以一个权重，最终将各个类别的加权票数求和，最大的值对应的类别为最终类别。

6.3 学习法

上两节的方法都是对弱学习器的结果做平均或者投票，相对比较简单，但是可能学习误差较大，于是就有了学习法这种方法，对于学习法，代表方法是stacking，当使用stacking的结合策略时，我们不是对弱学习器的结果做简单的逻辑处理，而是再加上一层学习器，也就是说，我们将训练集弱学习器的学习结果作为输入，将训练集的输出作为输出，重新训练一个学习器来得到最终结果。

在这种情况下，我们将弱学习器称为初级学习器，将用于结合的学习器称为次级学习器。对于测试集，我们首先用初级学习器预测一次，得到次级学习器的输入样本，再用次级学习器预测一次，得到最终的预测结果。

参考

上次更新: 2025/06/25, 11:25:50

← 零样本学习决策树→