1.回顾贝叶斯定理

首先，我们先来复习一下贝叶斯定理：

$$p(\mathrm{\Theta }|X)=\frac{p(X|\mathrm{\Theta })p(\mathrm{\Theta })}{p(X)}$$

在这个简简单单的式子当中，蕴含了我们要掌握的很多重要内容：

$p(\mathrm{\Theta })$ ：先验分布。 反映的是在观测到数据之前我们对待估计的参数 $\mathrm{\Theta }$ 的了解和认识。

$p(X|\mathrm{\Theta })$ ： 在确定了参数的情况下，试验数据的概率分布。实际上这就是对实际观测数据的一种描述。

$p(\mathrm{\Theta }|X)$ ：后验分布。 后验分布就是我们通过贝叶斯定理得到的最终的分析结果，反映的是在给定观测数据的基础上，我们对于参数的新的认知。说的更直白一点，就是最开始没有观测数据的时候，我们依据以往的经验赋予了参数一个先验分布，然后来了实际的观测数据之后，我们就对先验进行了更新，得到了这次分析过程的后验分布。

$p(X)$ ：边缘概率。 这是一个与我们待估计的参数 $\mathrm{\Theta }$ 无关的一个边缘概率值： $p(X)=\sum _{\theta }p(X,\mathrm{\Theta })=\sum _{\theta }p(X|\mathrm{\Theta })p(\mathrm{\Theta })$ ，因此我们并不用太关心这个值，仅仅把他当做是后验概率 $p(\mathrm{\Theta }|X)$ 算过程中的归一化系数即可。

因此我们更需要聚焦的就是如下的这个正比关系：$p(\mathrm{\Theta }|X)\propto p(X|\mathrm{\Theta })p(\mathrm{\Theta })$

实际上，有一个概念需要大家树立，那就是后验分布也是不断的处在动态更新过程当中的。一次试验得到的后验分布，对于后续进一步收集到的新的观测数据，他又可以看作是后续分析的一个先验。

2.贝叶斯推断与后验分布

在贝叶斯推断中，我们将待估计的量记为 $\mathrm{\Theta }$ ，视其为一个随机变量，我们的目标就是基于观测到的样本数据值 $X=(X_1,X_2,...,X_n)$ 来提取 $\mathrm{\Theta }$ 的信息，我们称 $X=(X_1,X_2,...,X_n)$ 为观测值，那么我们需要首先知道或者明确以下两方面内容：

第一个是视作随机变量 $\mathrm{\Theta }$ 的待估计未知参数的先验分布 $p_{\mathrm{\Theta }}$​，如果 $\mathrm{\Theta }$ 是连续的则相应的记作是 $f_{\mathrm{\Theta }}$ 。

第二个是基于参数 $\mathrm{\Theta }$ 的观测数据的分布模型，也就是条件分布 $p_{X|\mathrm{\Theta }}$​或者说是 $f_{X|\mathrm{\Theta }}$ ​，当然这取决于 $\mathrm{\Theta }$ 是连续型还是离散型随机变量。

一旦确立了 $X$ 的观测值 $x$ ，贝叶斯推断的完整答案就由随机变量 $\mathrm{\Theta }$ 的后验分布 $p_{\mathrm{\Theta }|X}(\theta |x)$ 或者 $f_{\mathrm{\Theta }|X}(\theta |x)$ 来描述和决定，这个后验分布的计算就是依赖贝叶斯定理来进行的。后验分布的精髓就在于他利用已经得知的观测数据，抓住了关于 $\mathrm{\Theta }$ 的一切信息。

3.贝叶斯推断求解过程

这里我们总结一下上述的整个过程：

首先，贝叶斯推断的起点是未知随机变量 $\mathrm{\Theta }$ 的先验分布 $p_{\mathrm{\Theta }}$​或者 $f_{\mathrm{\Theta }}$ ​。

然后，我们需要确定观测数据 $X$ 的分布模型，他是一个基于随机变量 $\mathrm{\Theta }$ 的条件概率： $p_{X|\mathrm{\Theta }}$ ​或者 $f_{X|\mathrm{\Theta }}$​。

一旦我们观察到了 $X$ 的一个特定值 $x$ 之后，我们就可以开始运用贝叶斯法则去计算 $\mathrm{\Theta }$ 的后验分布：

$$p_{\mathrm{\Theta }|X}(\theta |x)=\frac{p_{\mathrm{\Theta }}(\theta )p_{X|\mathrm{\Theta }}(x|\theta )}{p_X(x)}=\frac{p_{\mathrm{\Theta }}(\theta )p_{X|\mathrm{\Theta }}(x|\theta )}{\sum _{{\theta }^{\prime }}{p}_{\mathrm{\Theta }}({\theta }^{\prime })p_{X|\mathrm{\Theta }}(x|{\theta }^{\prime })}$$

如果是连续型的随机变量，就把上面的概率质量函数替换成概率密度函数就可以了。

4.贝叶斯推断实际举例

感觉说来说去，还是比较理论，很多量该怎么确定可能还是不知道如何下手。那么我们通过一个抛掷硬币的例子来把贝叶斯推断的过程演练一遍：

假设我们有一个并不均匀的硬币，投掷出正面和反面的概率并不是相等的0.5，因此我们通过不断的进行硬币抛掷试验来估计正面的概率 $\theta$ 。

那么我们首先为 $\theta$ 选择一个先验分布，实际上，我们对他一无所知，只知道这个 $\theta$ 应该介于 $[0,1]$ 之间，这个范围很粗犷，因此我们选择 $beta$ 分布作为参数 $\theta$ 的先验分布。

4.1. $beta$ 先验分布

$beta$ 分布是一个连续型随机变量的分布，他的概率密度函数为：

$$f(\theta )=\frac{\mathrm{\Gamma }(\alpha +\beta )}{\mathrm{\Gamma }(\alpha )\mathrm{\Gamma }(\beta )}{\theta }^{\alpha -1}(1-\theta {)}^{\beta -1}$$

这个先验分布我们之前很少接触，除了未知参数 $\theta$ 以外，他还有两个参数 $\alpha$ 和 $\beta$ ，用来控制整个 $beta$ 分布的图像，并且分式 $\frac{\mathrm{\Gamma }(\alpha +\beta )}{\mathrm{\Gamma }(\alpha )\mathrm{\Gamma }(\beta )}$ ​中间含有复杂的伽马函数。

其实这个分式大家不用特别关心，他可以被理解为一个正则项，保证整个概率密度函数的积分为1即可。

那么我们为什么要选择 $beta$ 分布作为未知参数 $\theta$ 的先验分布呢？相信大家都有疑问，那么我们通过下面的内容讲解来慢慢揭示，首先我们来看一下 $beta$ 分布的具体形态。

我们刚刚说过， $beta$ 分布概率密度函数中，参数 $\alpha$ 和参数 $\beta$ 是用来控制分布的形状的，具体指的什么，我们让参数 $\alpha$ 和参数 $\beta$ 分别依次从 $[0.25,1,10]$ 中取值作为参数，这样就构成了9组参数对，我们来依次画出他们的分布形态。

代码片段：

import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import beta
import seaborn
seaborn.set()

params = [0.25, 1, 10]
x = np.linspace(0, 1, 100)
f, ax = plt.subplots(len(params), len(params), sharex=True, sharey=True)

for i in range(len(params)):
    for j in range(len(params)):
        a = params[i]
        b = params[j]
        y = beta(a, b).pdf(x)
        ax[i, j].plot(x, y, color='red')
        ax[i, j].set_title('$\\alpha$={},$\\beta={}$'.format(a, b))
        ax[i, j].set_ylim(0, 10)
        
ax[0, 0].set_xticks([0, 0.2, 0.4, 0.6, 0.8, 1])
ax[0, 0].set_yticks([0, 2.5, 5, 7.5,  10])
ax[1, 0].set_ylabel('$p(\\theta)$')
ax[2, 1].set_xlabel('$\\theta$')
plt.show()

运行结果：

参数 $\alpha$ 和 $\beta$ 的不同取值组合，我们能够得到类似于 $U$ 型分布，正态分布，均匀分布，指数分布等等许多不同分布的形状，具有很强的通用性和适应性。

其次一点是共轭性，他能够极大的简化后验分布的计算，这一点我们接下来继续展开。

4.2.关于观测数据的分布

接下来，我们选择观测数据的分布，在抛掷硬币的过程中，确定了某一次抛掷硬币正面向上的概率 $\theta$ 之后，抛掷 $n$ 次硬币，其中 $y$ 次向上的概率是满足二项分布的，这个我们之前也反复讲过：

$$p(y|\theta )=\frac{n!}{y!(n-y)!}{\theta }^y(1-\theta {)}^{n-y}$$

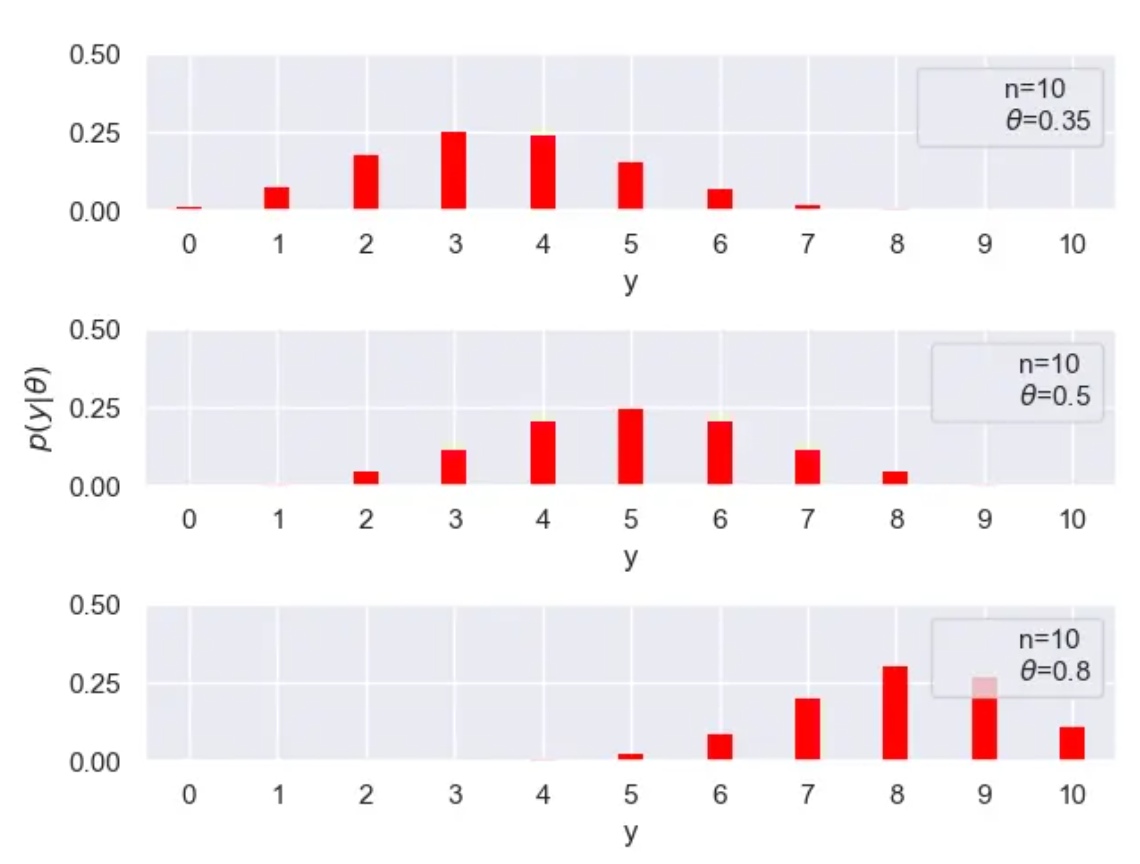
这里我们就抛掷10次硬币，其中令正面向上的概率分别是0.35,0.5,0.8，来看看观测数据所服从的分布：

代码片段：

from scipy.stats import binom
import matplotlib.pyplot as plt
import numpy as np
import seaborn

seaborn.set()

n = 10
p_params = [0.35, 0.5, 0.8]
x = np.arange(0, n + 1)
f, ax = plt.subplots(len(p_params), 1)

for i in range(len(p_params)):
    p = p_params[i]
    y = binom(n=n, p=p).pmf(x)
    
    ax[i].vlines(x, 0, y, colors='red', lw=10)
    ax[i].set_ylim(0, 0.5)
    ax[i].plot(0, 0, label='n={}\n$\\theta$={}'.format(n, p), alpha=0)
    ax[i].legend()
    ax[i].set_xlabel('y')
    ax[i].set_xticks(x)

ax[1].set_ylabel('$p(y|\\theta)$')
plt.show()

运行结果：

4.3.后验的计算

我们接下来就来计算后验：

$$f(\theta |y)\propto f(\theta )p(y|\theta )\$4\$\$f(\theta )=\frac{\mathrm{\Gamma }(\alpha +\beta )}{\mathrm{\Gamma }(\alpha )\mathrm{\Gamma }(\beta )}{\theta }^{\alpha -1}(1-\theta {)}^{\beta -1}$$$$p(y|\theta )=\frac{n!}{y!(n-y)!}{\theta }^y(1-\theta {)}^{n-y}$$

因此： $f(\theta |y)\propto \frac{\mathrm{\Gamma }(\alpha +\beta )}{\mathrm{\Gamma }(\alpha )\mathrm{\Gamma }(\beta )}{\theta }^{\alpha -1}(1-\theta {)}^{\beta -1}\frac{n!}{y!(n-y)!}{\theta }^y(1-\theta {)}^{n-y}$

而针对选定的先验，参数 $\alpha$ 和 $\beta$ 是已知的，针对一组已知的观测数据，抛掷的次数 $n$ 和正面向上的次数 $y$ 也是已知的，因此 $ \frac{\Gamma(\alpha+\beta)}{\Gamma(\alpha)\Gamma(\beta)}$​和 $\frac{n!}{y!(n-y)!}$ ​都是与未知参数 $\theta$ 无关的项，他们可以被合并到归一化项当中去，因此我们可以进一步化简：

$$f(\theta |y)\propto {\theta }^{\alpha -1}(1-\theta {)}^{\beta -1}{\theta }^y(1-\theta {)}^{n-y}={\theta }^{\alpha +y-1}(1-\theta {)}^{\beta +n-y-1}$$

最终实际的后验 $f(\theta |y)$ 就是在 ${\theta }^{\alpha +y-1}(1-\theta {)}^{\beta +n-y-1}$ 的基础上加上一个归一化的项，使之在整个 $\theta$ 的取值域上积分为1。

此时你可能会问，后面我们再该怎么处理？我们从后验分布的概率密度函数的正比表达式： ${\theta }^{\alpha +y-1}(1-\theta {)}^{\beta +n-y-1}$ 中惊奇的发现，后验分布同样也是一个 $beta$ 分布，只不过这个 $beta$ 分布的参数变了：

$${\alpha }_{posterior}=\alpha +y\$\${\beta }_{posterior}=\beta +n-y$$

那么我们很容易就能根据先验分布和观测数据得到后验分布了。

5.模拟实验验证

首先我们写一段模拟抛硬币的程序，我们手上的这枚硬币，正面向上的实际概率为0.62，我们模拟随机抛掷1000次硬币的试验，并且记录抛掷过程中，抛掷次数为 $[5,10,20,100,500,1000]$ 时，正面出现的次数。这个0.62就是我们需要根据观测数据来估计的未知参数，并且我们可以用它来和估计值进行对比。

代码片段：

import random

def bernoulli_trial(p):
    u = random.uniform(0, 1)
    if u <= p:
        return 1
    else:
        return 0

def coin_experiments(n_array, p):
    y = 0
    n_max = max(n_array)
    results = []
    for n in range(1, n_max+1):
        y = y + bernoulli_trial(p)
        if n in n_array:
            results.append((y, n))
    
    return results

print(coin_experiments([5, 10, 20, 100, 500, 1000], 0.62))

运行结果：

[(2, 5), (4, 10), (11, 20), (60, 100), (306, 500), (614, 1000)]

这个结果中，每一个元组表示的含义为(正面的次数，试验的次数)，记录了完成1000次试验的过程中，抛掷到5次，10次，20次，100次，500次和1000次的时候，相应的正面向上的次数。

例如 $(311,500)$ 表示当试验进行了500次时，正面出现的次数为311次。

请大家放心的是，这个试验生成的结果完全是按照伯努利试验随机生成的，你可以再重复运行5次该实验，一定会得到完全不同的5组试验结果：

代码片段：

for i in range(5):
    print(coin_experiments([5, 10, 20, 100, 1000, 10000], 0.62))

运行结果：

[(3, 5), (7, 10), (13, 20), (55, 100), (306, 500), (622, 1000)]
[(4, 5), (6, 10), (12, 20), (68, 100), (319, 500), (632, 1000)]
[(2, 5), (6, 10), (12, 20), (57, 100), (319, 500), (645, 1000)]
[(4, 5), (7, 10), (14, 20), (64, 100), (309, 500), (626, 1000)]
[(4, 5), (8, 10), (15, 20), (56, 100), (309, 500), (607, 1000)]

最后，我们利用三组 $(\alpha ,\beta )$ 分别为 $(0.25,0.25),(1,1),(10,10)$ 的 $beta$ 分布作为先验分布：

代码片段：

import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import beta
import seaborn
seaborn.set()

params = [0.25, 1, 10]
x = np.linspace(0, 1, 100)

plt.plot(x, beta(0.25, 0.25).pdf(x), color='b', label='$\\alpha=0.25,\\beta=0.25$')
plt.fill_between(x, 0, beta(0.25, 0.25).pdf(x), color='b', alpha=0.25)

plt.plot(x, beta(1, 1).pdf(x), color='g',label='$\\alpha=1,\\beta=1$')
plt.fill_between(x, 0, beta(1, 1).pdf(x), color='g', alpha=0.25)

plt.plot(x, beta(10, 10).pdf(x), color='r',label='$\\alpha=10,\\beta=10$')
plt.fill_between(x, 0, beta(10, 10).pdf(x), color='r', alpha=0.25)

plt.gca().axes.set_ylim(0,10)
plt.gca().axes.set_xlabel('$\\theta$')
plt.gca().axes.set_ylabel('$p(\\theta)$')
plt.legend()
plt.show()

运行结果：

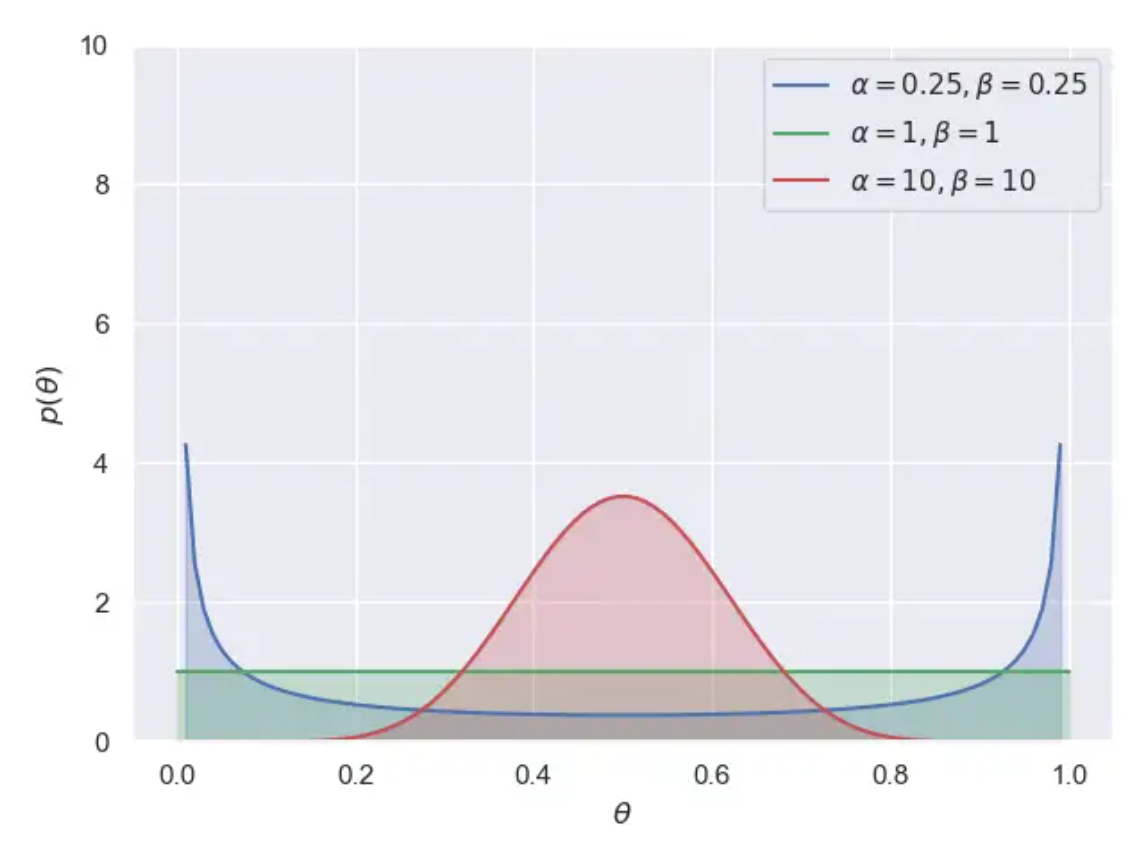
我们选择：

$[(2,5),(4,10),(11,20),(60,100),(306,500),(614,1000)]$ 作为观测数据，利用贝叶斯推断的方法，来得到后验分布

代码片段：

from scipy.stats import beta
import matplotlib.pyplot as plt
import numpy as np
import seaborn

seaborn.set()

theta_real = 0.62
n_array = [5, 10, 20, 100, 500, 1000]
y_array = [2, 4, 11, 60, 306, 614]

beta_params = [(0.25, 0.25), (1, 1), (10, 10)]
x = np.linspace(0, 1, 100)

fig, ax = plt.subplots(2, 3, sharex=True, sharey=True)

for i in range(2):
    for j in range(3):
        n = n_array[3 * i + j]
        y = y_array[3 * i + j]
        for (a_prior, b_prior), c in zip(beta_params, ('b', 'r', 'g')):
            a_post = a_prior + y
            b_post = b_prior + n - y
            p_theta_given_y = beta.pdf(x, a_post, b_post)
            ax[i, j].plot(x, p_theta_given_y, c)
            ax[i, j].fill_between(x, 0, p_theta_given_y, color=c, alpha=0.25)
	
        ax[i, j].axvline(theta_real, ymax=0.5, color='k')
        ax[i, j].set_xticks([0, 0.2, 0.4, 0.6, 0.8, 1])
        ax[i, j].set_title('n={},y={}'.format(n, y))

ax[0, 0].set_ylabel('$p(\\theta|y)$')
ax[1, 0].set_ylabel('$p(\\theta|y)$')
ax[1, 1].set_xlabel('$\\theta$')
plt.show()

运行结果：

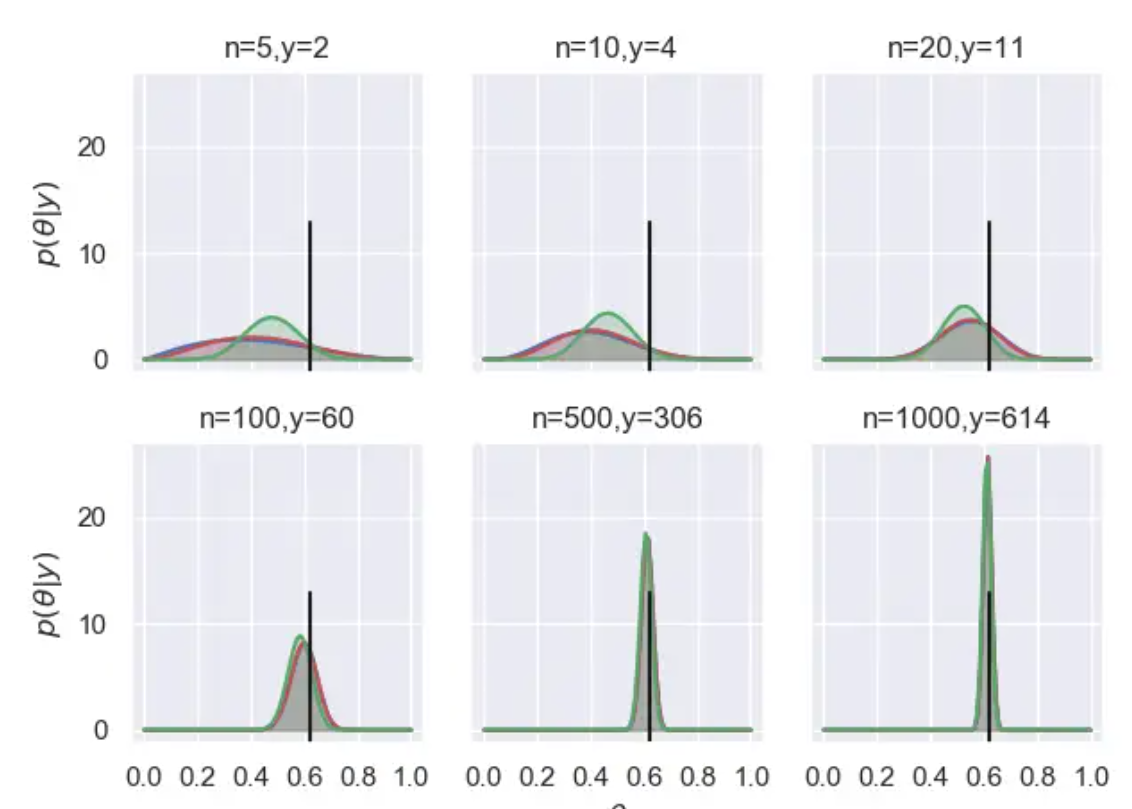
6.实验结果分析

我们来分析一下试验结果，首先我们设置了三种典型的先验分布，均匀分布、 $U$ 型分布和类似正态分布，分别代表了我们对于未知参数 $\theta$ 不同的认识，比如如果我们选择均匀分布，意味着我们认为， $\theta$ 在 $[0,1]$ 范围内的取值是等概率的； $U$ 型分布代表了在靠近0和1的两头， $\theta$ 的取值概率越高，类正态分布表示我们认为越靠近中心0.5的位置，取值概率越高。这三者的认识是截然不同的。

在整个实验的每一个阶段，通过先验分布与观测数据的综合，我们得到了每个阶段的后验结果，我们从图中可以看出，贝叶斯推断得到的是一个后验分布，而不像极大似然估计中得到的是一个具体值。他表示了在给定观测数据的情况下，推断得到的未知参数 $\theta$ 的分布情况。

一般而言我们都会选择后验分布概率密度函数曲线的峰值作为我们最终对于未知参数的估计值。这就是贝叶斯推断中的最大后验概率（ $MAP$ ）准则，即选择在一个给定数据下，具有最大后验概率的值。

从这个结果图中，我们可以看出很多的结论：

首先，随着观测数据的不断增多，后验分布会越来越集中，分布越集中表示对于参数的确定性越高，这很显然，观测数据的增多意味着有更多的数据、更多的信息来更新和支撑我们对于参数的认识。

其次，当观测数据的量足够多的时候，不同的先验分布对应的后验分布都会收敛到一个相同的结果，数据越多，通过最大后验概率准则得到的估计值就会与参数的实际值（黑色竖线）越接近。

7.关于共轭先验的问题

那么这里有一个重要的点要强调，当然也是我们当初没有谈到的，先验选择 $beta$ 分布的第三个好处，那就是：

先验分布是 $beta$ 分布，观测数据服从二项分布，得到的后验仍然是 $beta$ 分布，也就是说 $beta$ 分布是二项分布的共轭先验：即将先验 $beta$ 分布与二项分布组合在一起之后，得到的后验分布与先验分布的表达式形式仍然是一样的。除此之外，正态分布也是自身的共轭先验。

这种分布的共轭特性，极大的简化了我们求解后验分布的计算复杂性。但是，共轭分布的情形并不普遍，因此如果不是在共轭先验的条件下去解决贝叶斯推断问题，那么在计算后验分布的过程中将会遇到非常大的困难，后验分布绝大多数情况下就不再是一个标准分布，甚至没有解析解，在这种情况下想了解后验分布的形态将遇到巨大的挑战，基于他去做后续的统计分析将难上加难。

---

先验分布与后验分布

什么是贝叶斯统计？

贝叶斯统计的重要特点在于，我们在建模前需要给出模型参数 $\theta$ 的先验分布（prior distribution） $p(\theta )$ 。也就是说，在得到任何数据，或者将任何数据对模型进行拟合之前，我们需要先给定模型参数服从的分布。例如，对于抛掷一枚硬币一次可能出现的结果，我们可以构建一个参数为 $\theta$ 的伯努利分布概率模型 $X\sim bernoulli(\theta )$ 。那么在使用数据估计参数 $\theta$ 之前，我们需要给这个参数设定一个分布（注意，先验分布是关于模型参数的分布，而不是我们建模的对象本身，下文中将要介绍的后验分布，也是关于模型参数的分布）。给出参数的先验分布，是贝叶斯统计的核心部分之一，也是对于长期接触频率学派思想的贝叶斯初学者来说最容易困惑的部分：没有数据的支持，在贝叶斯统计中的先验分布到底如何设定？

实际上，先验分布的存在正是贝叶斯学派相对于频率学派更贴近实际问题的一点。虽然理论上我们在利用现有数据之前，不存在任何数据支持我们对 $\theta$ 做出假设，但在现实中，我们对我们要建模的目标总会存在一些经验判断。由此，我们可以在利用数据来估计 $\theta$ 之前，将我们的实际经验作为有价值的信息加入到模型参数的估计过程当中。

继续上面的例子，反复投掷同一枚硬币，我们通过常识可以知道其正面朝上的概率 $\theta$ 在 0.5 左右浮动。概率的浮动是由这一枚硬币的实际情况导致（密度均匀程度，以及外形是否完美等等）。由于先验分布可以是任意的，我们因此可以依据经验，假设先验分布则

$p(\theta )=4xI(0\le x<0.5)+4(1-x)I(0.5\le x\le 1).$

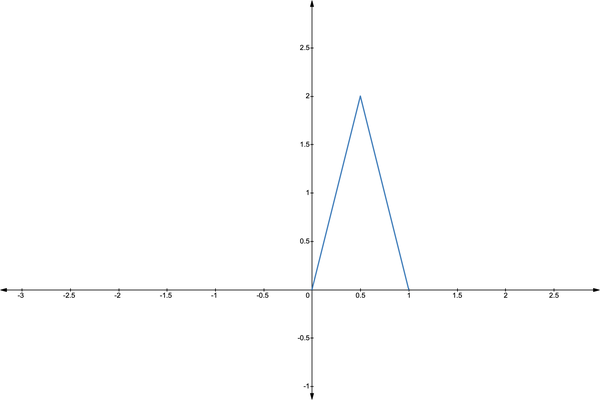
这是我随意举例的一个先验分布。理论上，我们可以使用任何的分布作为先验分布。但一个好的先验分布需要囊括我们对参数的经验判断信息，而上文构造的分布则成功包含了关于 $\theta$ 分布应有的部分特征：

1. 它当 $\theta =0.5$ 时概率密度最大，符合上文所描述的对硬币的认知。
2. 概率密度函数从 $\theta =0.5$ 处向两端递减，这同样具有现实意义。我们几乎不可能找到正面朝上概率为 $0.99$ 的硬币，甚至无法想象。

在得到了模型参数的先验分布之后，我们便可以通过样本数据 $x_1,...,x_n$ 来进一步更新模型参数的分布。这便是贝叶斯学派与频率学派的另一个重要的不同之处**：在贝叶斯统计中，数据被用于更新参数的分布，而非作为参数极大似然估计的组成部分。事实上，我们已经能够通过研究模型参数的先验分布 $p(\theta )$ ，了解 $\theta$ 的性质。而利用数据更新模型参数的分布，能够使我们更加充分地利用已知信息进行统计推断。更新模型参数分布的过程，本质上是在给定 $x_1,...,x_{10}$ 下得到的关于 $\theta$ 的新的分布，即 $p(\theta |x_1,...,x_{10})=p(\theta |X)$ ，其中 $p(\theta |X)$ 被称作 $\theta$ 的后验分布（posterior distribution）**。根据贝叶斯定理，我们有

$$p(\theta |X)=\frac{p(\theta ,X)}{p(X)}=\frac{p(X|\theta )p(\theta )}{{\int }_{-\mathrm{\infty }}^{+\mathrm{\infty }}p(X|\theta )p(\theta )d\theta }.$$

可以看到，通过贝叶斯公式，我们将 $\theta$ 的后验分布 $p(\theta |X)$ 与先验分布 $p(\theta )$ 结合在了一起。而在这个公式中，$p(X|\theta )$ 是在给定 $\theta$ 下关于数据样本的似然函数。对于初学者而言，这个公式可能仍然比较抽象。我们可以使用如下例子加以理解：若希望计算在给定了数据后 $\theta =0.5$ 的后验概率密度，利用上述公式，我们可以得到

$$p(\theta =0.5|X)=\frac{p(X|\theta =0.5)p(\theta =0.5)}{{\int }_{-\mathrm{\infty }}^{+\mathrm{\infty }}p(X|\theta )p(\theta )d\theta }.$$

事实上，我们可以发现式子中的 ${\int }_{-\mathrm{\infty }}^{+\mathrm{\infty }}p(X|\theta )p(\theta )d\theta$ 是某个常数 $c$ ，因此我们可以极大地化简我们后验分布的形式为

$$p(\theta |X)\propto p(X|\theta )p(\theta ).$$

我们只要对 $p(X|\theta )p(\theta )$ 稍加放缩，使 $p(\theta |X)$ 曲线下的面积等于1，即可以得到 $\theta$ 的后验分布概率密度函数(probability density function)。

下面是一个特殊的例子，能够帮助读者深化对于贝叶斯思想的印象：

Example

当我非常肯定，所有的硬币投掷正面朝上概率为0.5时，我可以设先验分布 $p(\theta =0.5)=1$ , 除此之外 $p(\theta )=0$ 。由于 $\theta$ 的后验分布表示如下：

$$p(\theta |X)\propto p(X|\theta )p(\theta ).$$

我们可以得出， $\theta \ne 0.5$ 的后验概率在任何 $X$ 下都等于 $0$ ，而 $\theta =0.5$ 的后验概率在任何 $X$ 下都等于 $1$ 。也就是说，当我们 $\theta$ 为 0.5 的概率为100%时，不论真实数据如何，都无法改变 $\theta$ 为0.5的概率为100%这一现状。这个例子的现实意义就在于，当我们对一个参数的值有百分百的自信时，再多数据都无法更新参数的后验分布。这是贝叶斯统计比较有意思的一点。

小结

事实上，本文所举的考察二项分布的参数 $\theta$ 是较为简单的应用情形，贝叶斯学派的这一套思想可以进一步用来研究泊松分布、指数分布、正态分布乃至线性回归模型；除此之外，本文所构造的先验分布也是相对随意的。在实际问题中，我们往往会构造共轭先验分布（conjugate prior distribution），保证我们在不断使用数据更新参数后验分布时，该分布与先验分布属于同一已知分布族当中。我们将在下一篇文章中介绍共轭先验分布，敬请期待。

附录

1. 贝叶斯公式

我们回忆贝叶斯公式的形式：

$$p(y_j|x)=\frac{p(x|y_j)p(y_j)}{\sum _{i=0}^{n}p(x|y_i)p(y_i)}$$

注意上式描述的是 $y$ 为离散的随机变量的情况，当 $y $ 服从连续分布时，公式改写为

$$p(y_0|x)=\frac{p(x|y_0)p(y_0)}{{\int }_{-\mathrm{\infty }}^{+\mathrm{\infty }}p(x|y)p(y)dy}$$

References

• 石溪 (opens new window)
• 走进贝叶斯统计（一）—— 先验分布与后验分布 (opens new window)