其他RNN

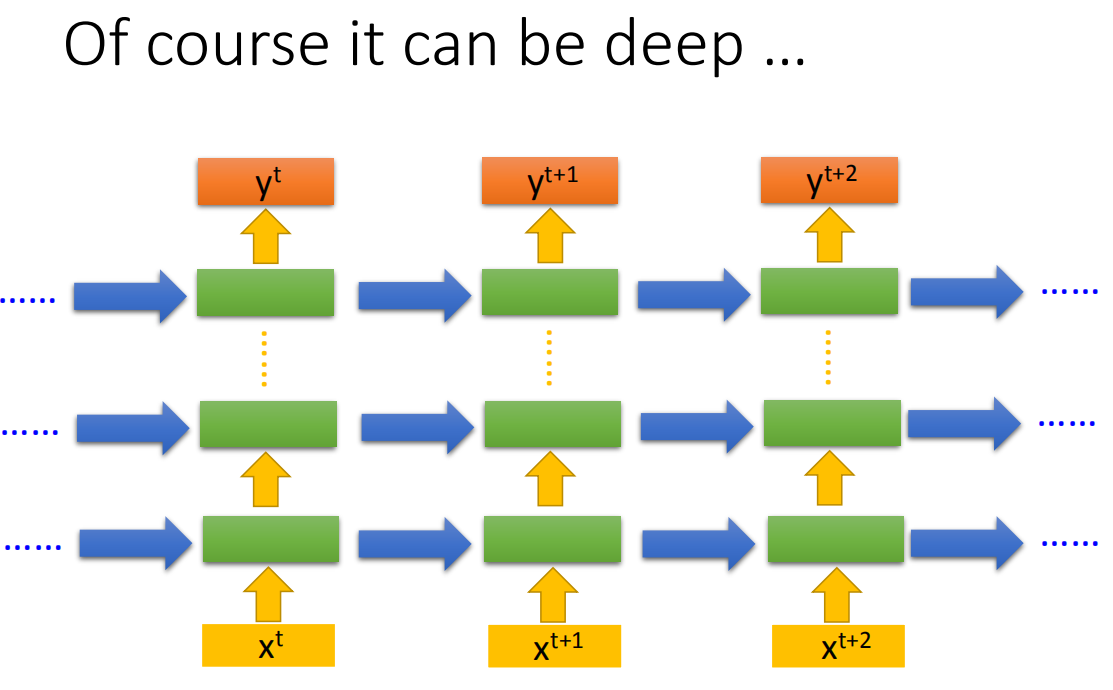
Recurrent Neural Networ的架构是可以任意设计的，比如说，它当然是deep(刚才我们看到的Recurrent Neural Networ它只有一个hidden layer)，当然它也可以是deep Recurrent Neural Networ。

比如说，我们把$x^t$ 进去之后，它可以通过一个hidden layer，再通过第二个hidden layer，以此类推(通过很多的hidden layer)才得到最后的output。每一个hidden layer的output都会被存在memory里面，在下一个时间点的时候，每一个hidden layer会把前一个时间点存的值再读出来，以此类推最后得到output，这个process会一直持续下去。

Elman network &Jordan network

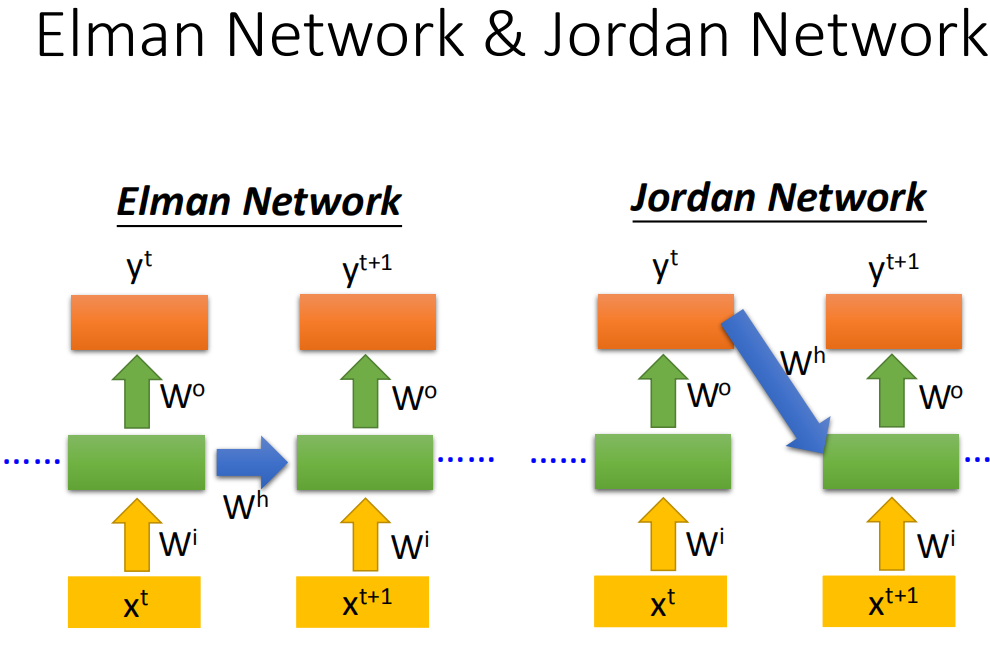
Recurrent Neural Networ会有不同的变形，我们刚才讲的是Elman network。(如果我们今天把hidden layer的值存起来，在下一个时间点在读出来)。还有另外一种叫做Jordan network，Jordan network存的是整个network output的值，它把output值在下一个时间点在读进来(把output存到memory里)。传说Jordan network会得到好的performance。

Elman network是没有target，很难控制说它能学到什么hidden layer information(学到什么放到memory里)，但是Jordan network是有target，今天我们比较很清楚我们放在memory里是什么样的东西。

Bidirectional neural network

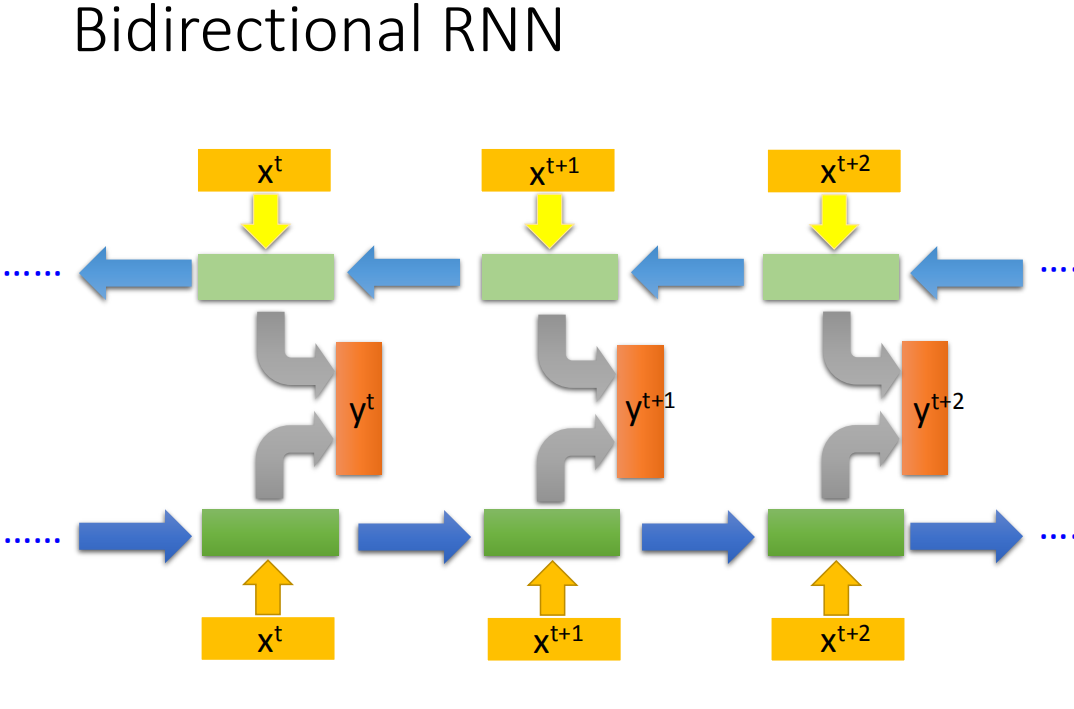
Recurrent Neural Networ还可以是双向，什么意思呢？我们刚才Recurrent Neural Networ你input一个句子的话，它就是从句首一直读到句尾。假设句子里的每一个词汇我们都有$x^t$ 示它。他就是先读$x^t$ 读$x^{t+1}$ 读$x^{t+2}$。但是它的读取方向也可以是反过来的，它可以先读$x^{t+2}$，再读$x^{t+1}$，再读$x^t$。你可以同时train一个正向的Recurrent Neural Network，又可以train一个逆向的Recurrent Neural Network，然后把这两个Recurrent Neural Network的hidden layer拿出来，都接给一个output layer得到最后的$y^t$。所以你把正向的network在input$x^t$ 时候跟逆向的network在input$x^t$ ，都丢到output layer产生$y^t$，然后产生$y^{t+1}$,$y^{t+2}$,以此类推。用Bidirectional neural network的好处是，neural在产生output的时候，它看的范围是比较广的。如果你只有正向的network，再产生$y^t$，$y^{t+1}$ 时候，你的neural只看过$x^1$ $x^{t+1}$ input。但是我们今天是Bidirectional neural network，在产生$y^{t+1}$ 时候，你的network不只是看过$x^1$,到$x^{t+1}$ 有的input，它也看了从句尾到$x^{t+1}$ input。那network就等于整个input的sequence。假设你今天考虑的是slot filling的话，你的network就等于看了整个sentence后，才决定每一个词汇的slot应该是什么。这样会比看sentence的一半还要得到更好的performance。

那我们刚才讲的Recurrent Neural Network其实是Recurrent Neural Network最单的版本

LSTM

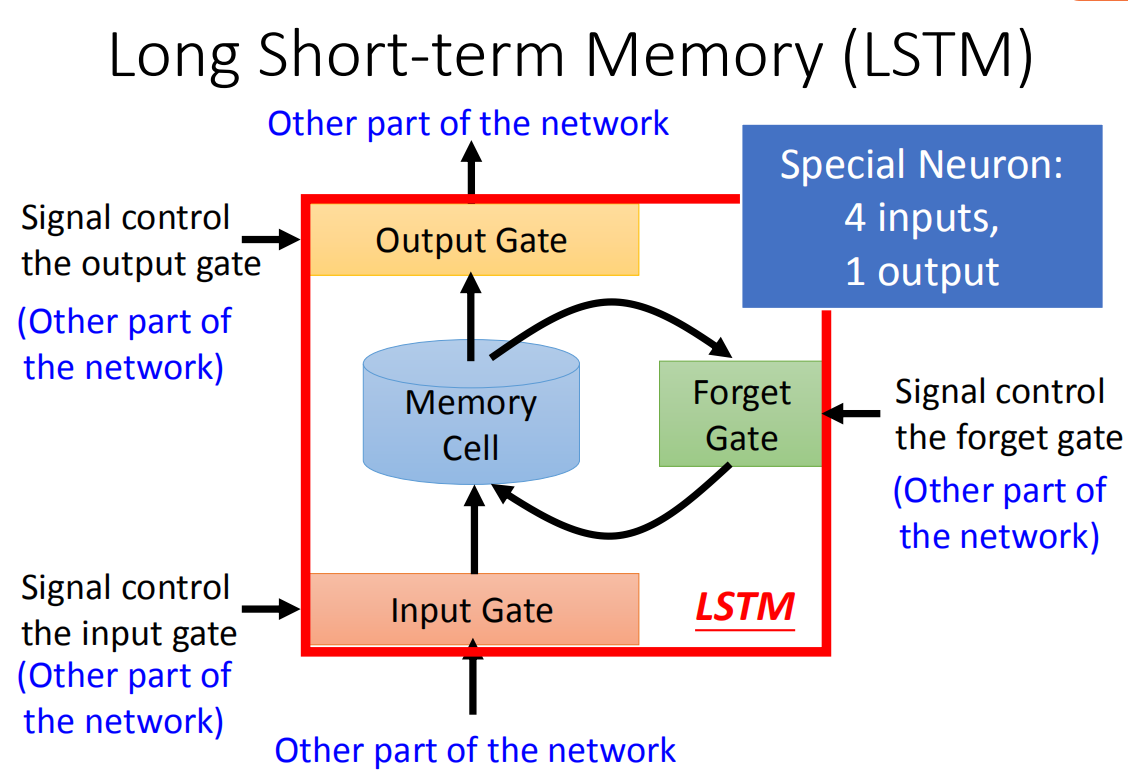
那我们刚才讲的memory是最单纯的，我们可以随时把值存到memory去，也可以把值读出来。但现在最常用的memory称之为Long Short-term Memory(长时间的短期记忆)，简写LSTM.这个Long Short-term Memor是比较复杂的。

这个Long Short-term Memor是有三个gate，当外界某个neural的output想要被写到memory cell里面的时候，必须通过一个input Gate，那这个input Gate要被打开的时候，你才能把值写到memory cell里面去，如果把这个关起来的话，就没有办法把值写进去。至于input Gate是打开还是关起来，这个是neural network自己学的(它可以自己学说，它什么时候要把input Gate打开，什么时候要把input Gate关起来)。那么输出的地方也有一个output Gate，这个output Gate会决定说，外界其他的neural可不可以从这个memory里面把值读出来(把output Gate关闭的时候是没有办法把值读出来，output Gate打开的时候，才可以把值读出来)。那跟input Gate一样，output Gate什么时候打开什么时候关闭，network是自己学到的。那第三个gate叫做forget Gate，forget Gate决定说：什么时候memory cell要把过去记得的东西忘掉。这个forget Gate什么时候会把存在memory的值忘掉，什么时候会把存在memory里面的值继续保留下来)，这也是network自己学到的。

那整个LSTM你可以看成，它有四个input 1个output，这四个input中，一个是想要被存在memory cell的值(但它不一定存的进去)还有操控input Gate的讯号，操控output Gate的讯号，操控forget Gate的讯号，有着四个input但它只会得到一个output

冷知识：这个“-”应该在short-term中间，是长时间的短期记忆。想想我们之前看的Recurrent Neural Network，它的memory在每一个时间点都会被洗掉，只要有新的input进来，每一个时间点都会把memory 洗掉，所以的short-term是非常short的，但如果是Long Short-term Memory，它记得会比较久一点(只要forget Gate不要决定要忘记，它的值就会被存起来)。

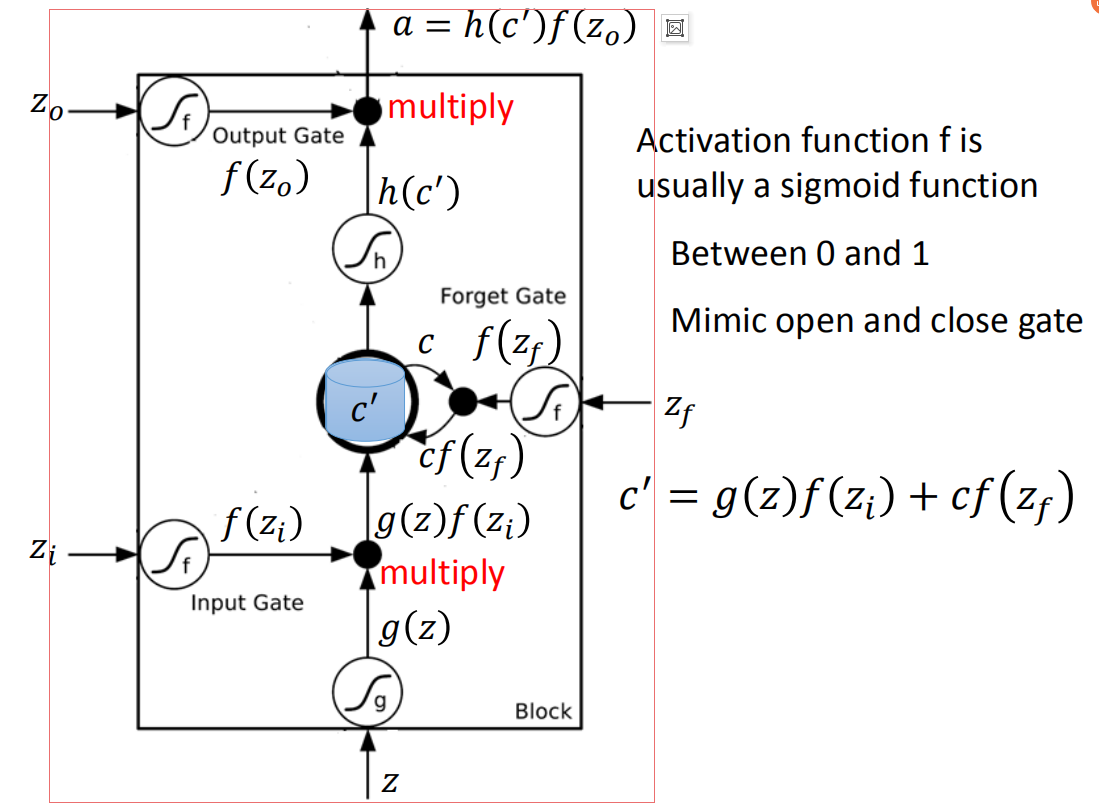这个memory cell更仔细来看它的formulation，它长的像这样。

底下这个是外界传入cell的input，还有input gate,forget gate,output gate。现在我们假设要被存到cell的input叫做z，操控input gate的信号叫做$z_i$（一个数值）,所谓操控forget gate的信号叫做$z_f$，操控output gate叫做$z_o$，综合这些东西会得到一个output 记为a。假设cell里面有这四个输入之前，它里面已经存了值c。

假设要输入的部分为z，那三个gate分别是由$z_i$,$z_f$,$z_0$ 操控的。那output a会长什么样子的呢。我们把z通过activation function得到g(z)，那$z_i$ 过另外一个activation function得到$f(z_i)$($z_i$,$z_f$,$z_0$ 过的activation function 通常我们会选择sigmoid function)，选择sigmoid function的意义是它的值是介在0到1之间的。这个0到1之间的值代表了这个gate被打开的程度(如果这个f的output是1，表示为被打开的状态，反之代表这个gate是关起来的)。

那接下来，把$g(z)$ 以$f(z_i)$ 到$g(z)f(z_i)$，对于forget gate的$z_f$,也通过sigmoid的function得到$f(z_f)$

接下来把存到memory里面的值c乘以$f(z_f)$ 到c$f(z_f)$，然后加起来$c^{{}^{\prime }}=g(z)f(z_i)+cf(z_f)$，那么$c^{{}^{\prime }}$ 是重新存到memory里面的值。所以根据目前的运算说，这个$f(z_i)$cortrol这个$g(z)$，可不可以输入一个关卡(假设输入$f(z_i)$0，\mathrm{那}$g(z)f(z_i)$ 等于0，那就好像是没有输入一样，如果$f(z_i)$ 于1就等于是把$g(z)$ 做输入) 。那这个$f(z_f)$ 定说：我们要不要把存在memory的值洗掉假设$f(z_f)$ 1(forget gate 开启的时候),这时候c会直接通过(就是说把之前的值还会记得)。如果$f(z_f)$ 于0(forget gate关闭的时候)$cf(z_f)$ 于0。然后把这个两个值加起来($c^{{}^{\prime }}=g(z)f(z_i)+cf(z_f)$)写到memory里面得到$c^{{}^{\prime }}$。这个forget gate的开关是跟我们的直觉是相反的，那这个forget gate打开的时候代表的是记得，关闭的时候代表的是遗忘。那这个$c^{{}^{\prime }}$ 过$h(c^{{}^{\prime }})$，将$h(c^{{}^{\prime }})$ 以$f(z_o)$ 到$a=f(c^{{}^{\prime }}f(z_o)$(output gate受$f(z_o)$ 操控，$f(z_o)$ 于1的话，就说明$h(c^{{}^{\prime }})$ 通过，$f(z_o)$ 于0的话，说明memory里面存在的值没有办法通过output gate被读取出来)

LSTM举例

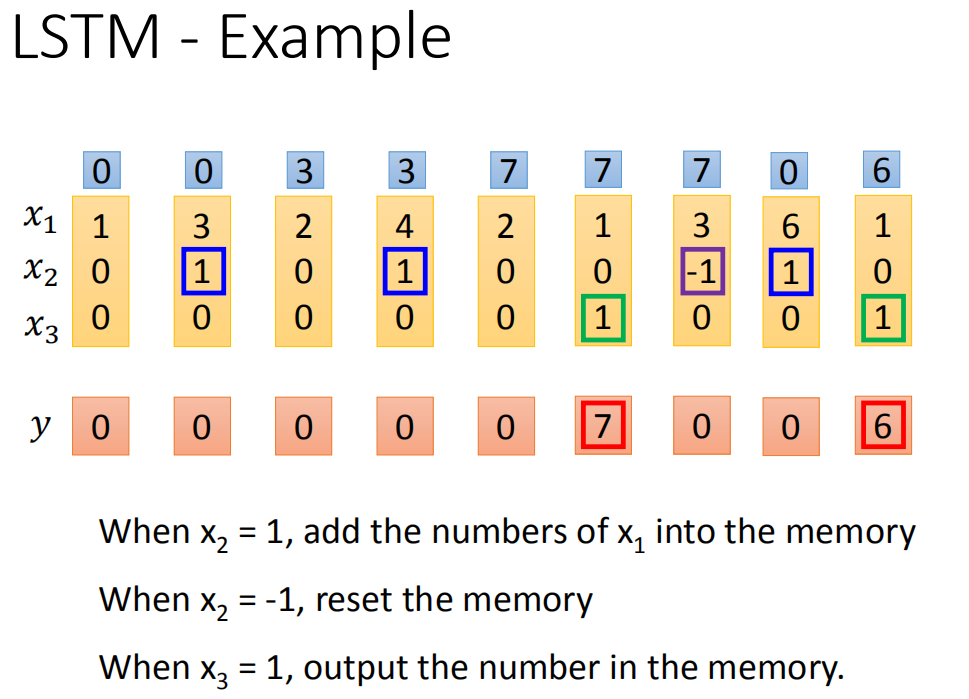LSTM例子:我们的network里面只有一个LSTM的cell，那我们的input都是三维的vector，output都是一维的output。那这三维的vector跟output还有memory的关系是这样的。假设第二个dimension$x_2$ 值是1时，$x_1$ 值就会被写到memory里，假设$x_2$ 值是-1时，就会reset the memory，假设$x_3$ 值为1时，你才会把output打开才能看到输出。

假设我们原来存到memory里面的值是0，当第二个dimension$x_2$ 值是1时，3会被存到memory里面去。第四个dimension的$x_2$ 于，所以4会被存到memory里面去，所以会得到7。第六个dimension的$x_3$ 于1，这时候7会被输出。第七个dimension的$x_2$ 值为-1，memory里面的值会被洗掉变为0。第八个dimension的$x_2$ 值为1，所以把6存进去，因为$x_3$ 值为1，所以把6输出。

LSTM运算举例

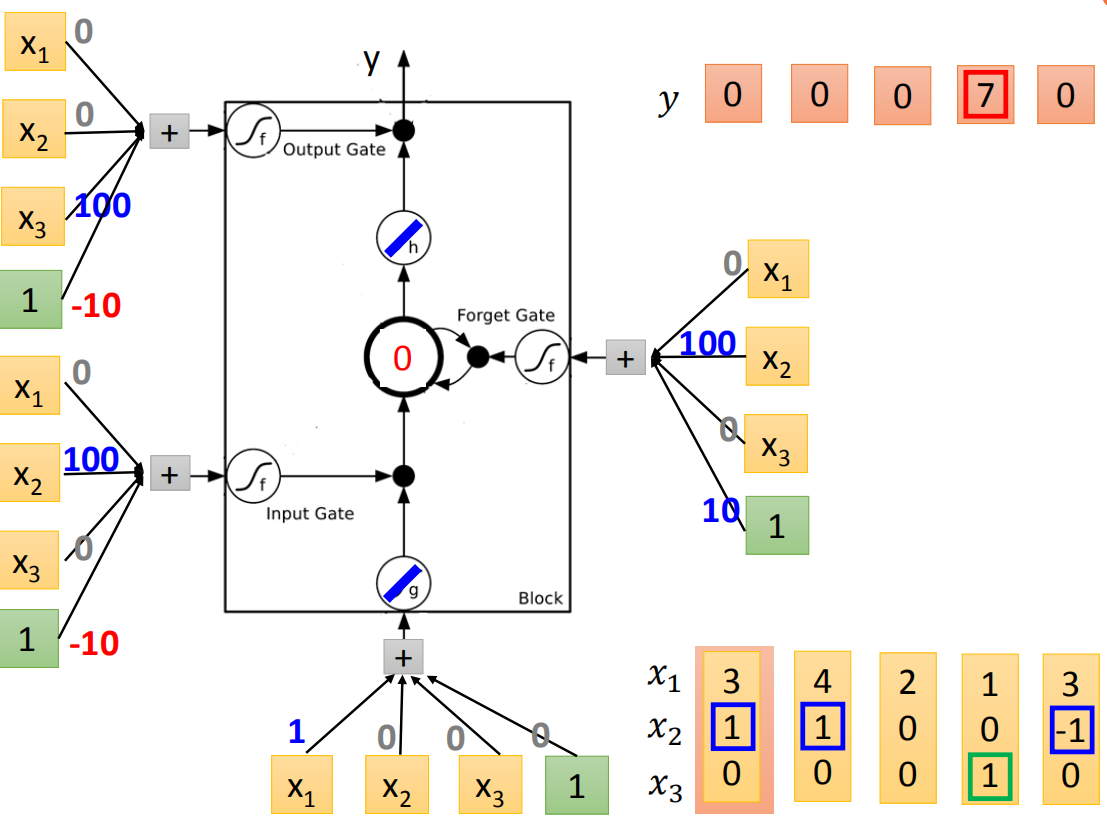那我们就做一下实际的运算，这个是一个memory cell。这四个input scalar是这样来的：input的三维vector乘以linear transform以后所得到的结果($x_1$,$x_2$,$x_3$ 以权重再加上bias)，这些权重和bias是哪些值是通过train data用GD学到的。 假设我已经知道这些值是多少了，那用这样的输入会得到什么样的输出。那我们就实际的运算一下。

在实际运算之前，我们先根据它的input，参数分析下可能会得到的结果。底下这个外界传入的cell，$x_1$ 以1，其他的vector乘以0，所以就直接把$x_1$ 做输入。在input gate时，$x_2$ 以100，bias乘以-10(假设$x_2$ 没有值的话，通常input gate是关闭的(bias等于-10)因为-10通过sigmoid函数之后会接近0，所以就代表是关闭的，若$x_2$ 值大于1的话，结果会是一个正值，代表input gate会被打开) 。forget gate通常会被打开的，因为他的bias等于10(它平常会一直记得东西)，只有当$x_2$ 值为一个很大的负值时，才会把forget gate关起来。output gate平常是被关闭的，因为bias是一个很大的负值，若$x_3$ 一个很大的正值的话，压过bias把output打开。

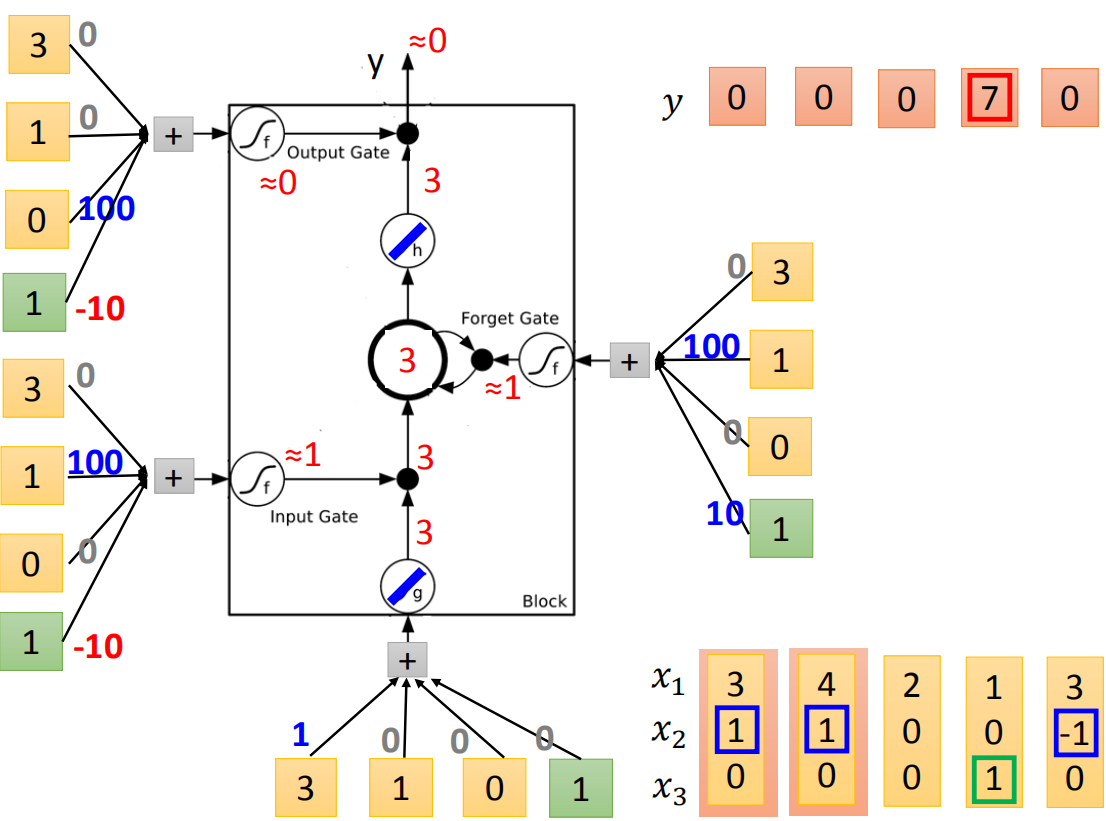接下来，我们实际的input一下看看。我们假设g和h都是linear(因为这样计算会比较方便)。假设存到memory里面的初始值是0，我们input第一个vector(3,1,0),input这边3*1=3，这边输入的是的值为3。input gate这边($1\ast 100-10\approx 1$)是被打开(input gate约等于1)。($g(z)\ast f(z_i)=3$)。forget gate($1\ast 100+10\approx 1$)是被打开的(forget gate约等于1)。现在0 *1+3=3($c^{{}^{\prime }}=g(z)f(z_i)+cf(z_f)$)，所以存到memory里面的现在为3。output gate(-10)是被关起来的，所以3无关通过，所以输出值为0。

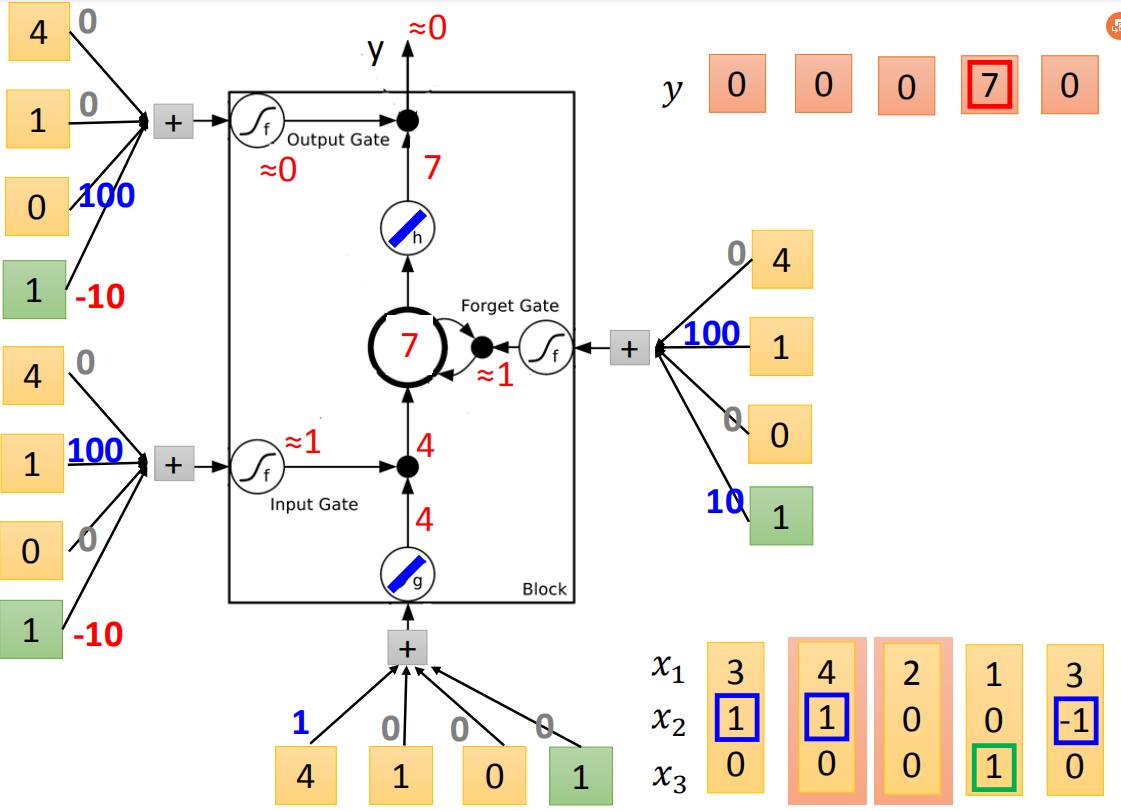接下来input(4,1,0),传入input的值为4，input gate会被打开，forget gate也会被打开，所以memory里面存的值等于7(3+4=7)，output gate仍然会被关闭的，所以7没有办法被输出，所以整个memory的输出为0。

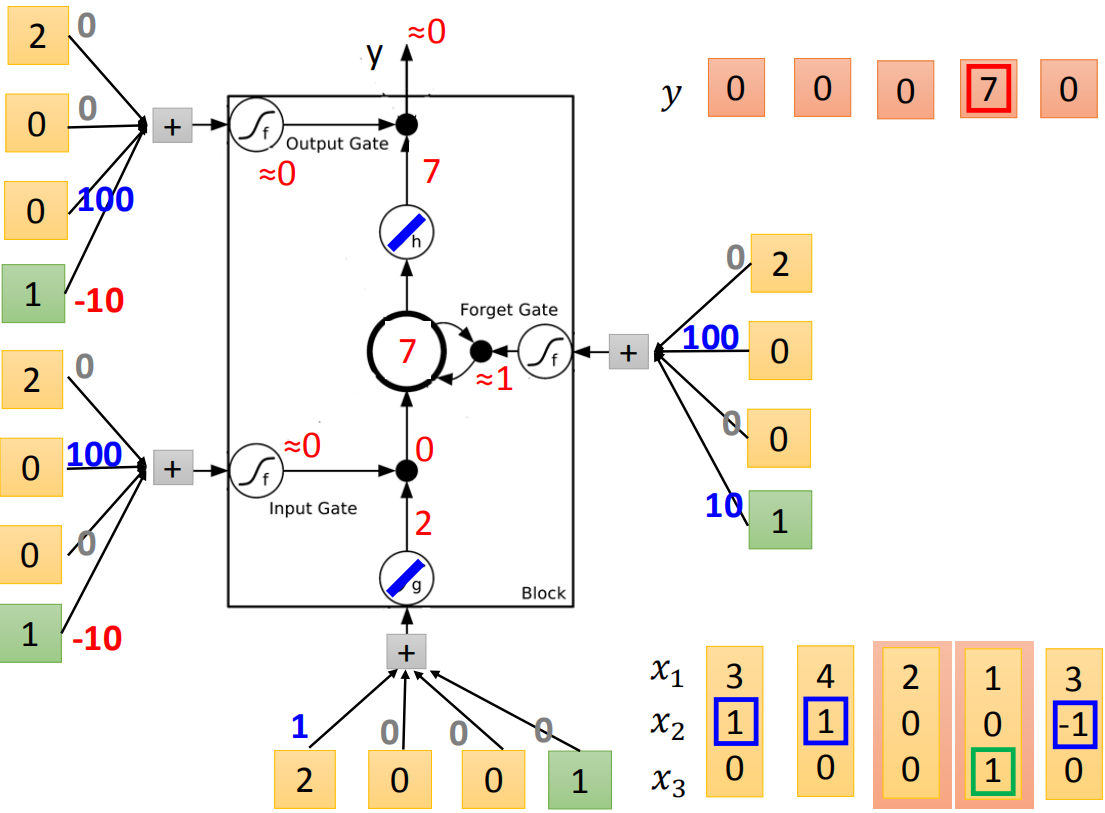
接下来input(2,0,0),传入input的值为2，input gate关闭($\approx$ 0),input被input gate给挡住了(0 *2=0),forget gate打开(10)。原来memory里面的值还是7(1 *7+0=7).output gate仍然为0，所以没有办法输出，所以整个output还是0。

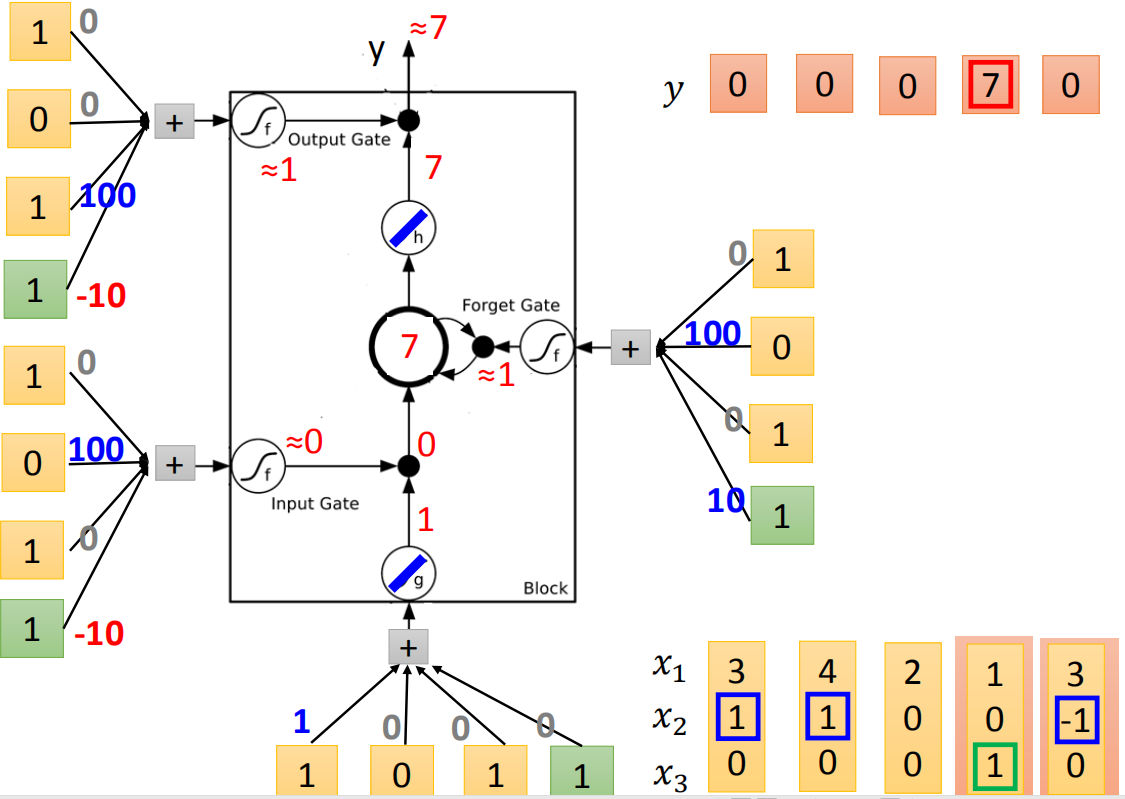接下来input(1,0,1),传入input的值为1,input gate是关闭的，forget gate是打开的，memory里面存的值不变，output gate被打开，整个output为7(memory里面存的7会被读取出来)

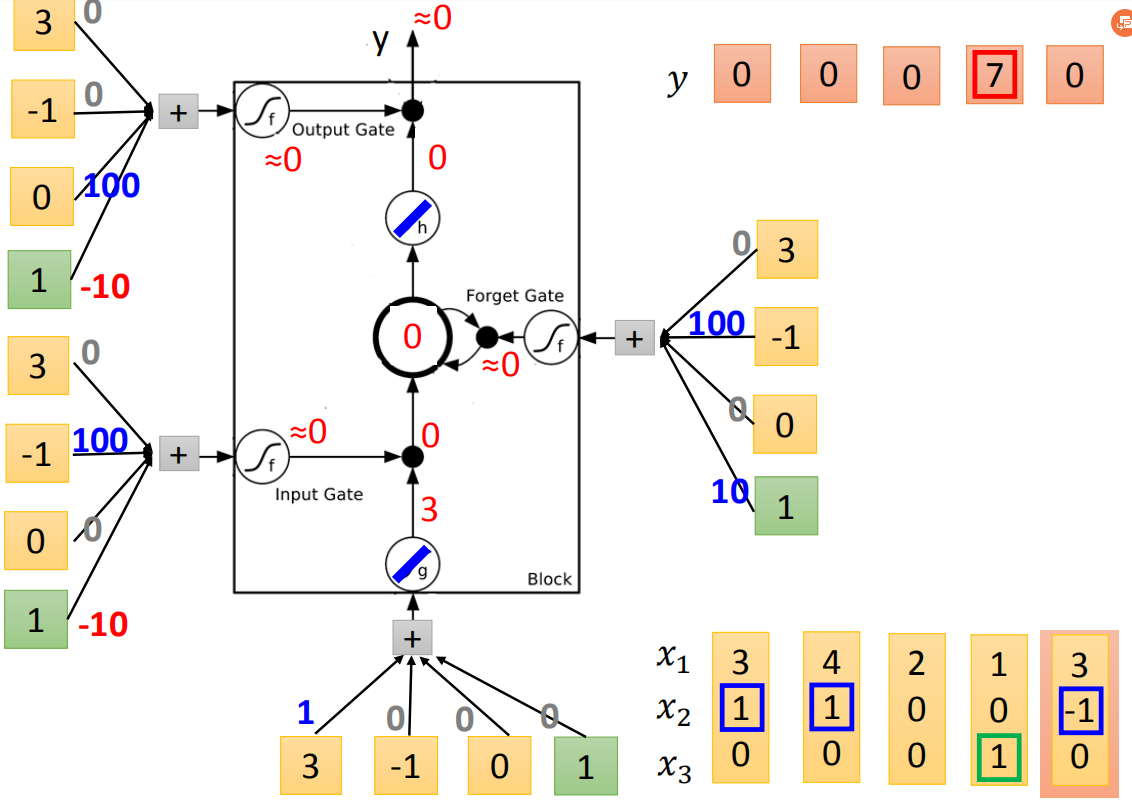最后input(3,-1,0),传入input的值为3，input gate 关闭，forget gate关闭，memory里面的值会被洗掉变为0，output gate关闭，所以整个output为0。

LSTM原理

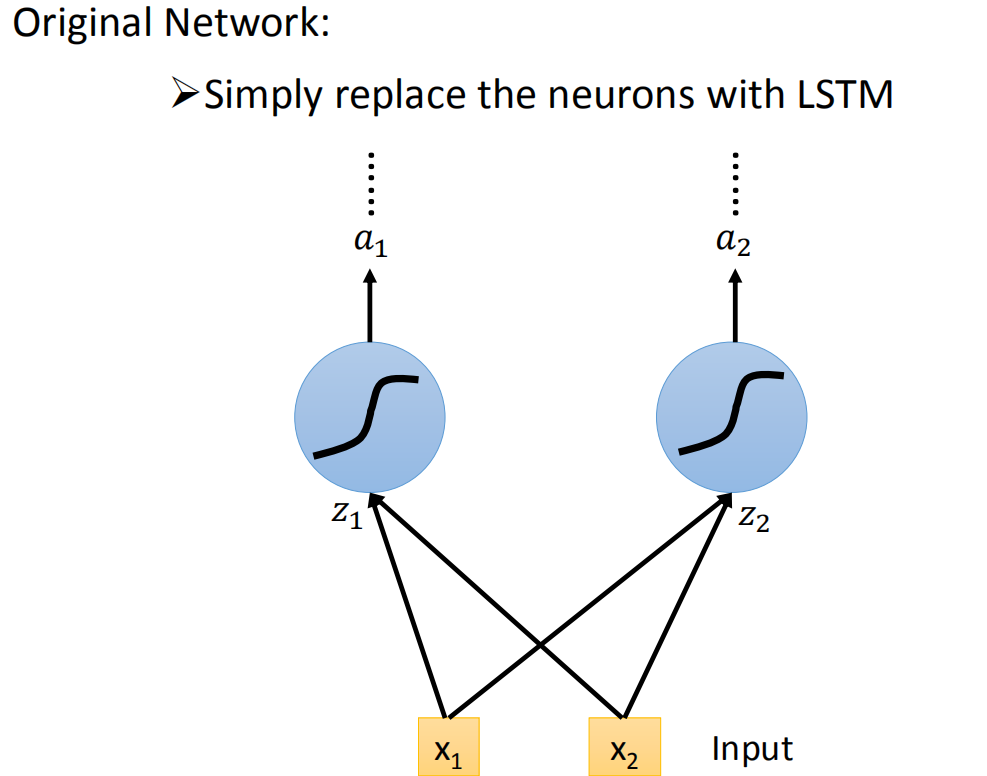你可能会想这个跟我们的neural network有什么样的关系呢。你可以这样想，在我们原来的neural network里面，我们会有很多的neural，我们会把input乘以不同的weight当做不同neural的输入，每一个neural都是一个function，输入一个值然后输出一个值。但是如果是LSTM的话，其实你只要把LSTM那么memory的cell想成是一个neuron就好了。

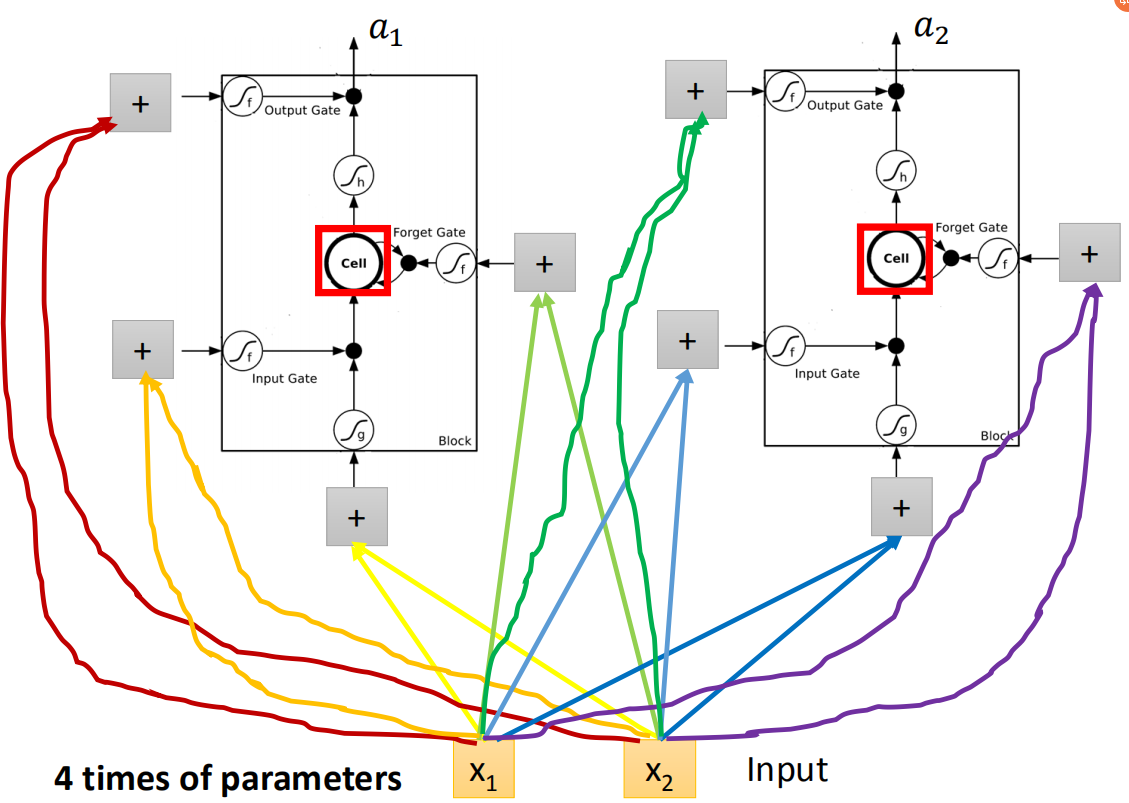
所以我们今天要用一个LSTM的neuron，你做的事情其实就是原来简单的neuron换成LSTM。现在的input($x_1,x_2$)会乘以不同的weight当做LSTM不同的输入(假设我们这个hidden layer只有两个neuron，但实际上是有很多的neuron)。input($x_1,x_2$)会乘以不同的weight会去操控output gate，乘以不同的weight操控input gate，乘以不同的weight当做底下的input，乘以不同的weight当做forget gate。第二个LSTM也是一样的。所以LSTM是有四个input跟一个output，对于LSTM来说，这四个input是不一样的。在原来的neural network里是一个input一个output。在LSTM里面它需要四个input，它才能产生一个output。

LSTM因为需要四个input，而且四个input都是不一样，原来的一个neuron就只有一个input和output，所以LSTM需要的参数量(假设你现在用的neural的数目跟LSTM是一样的)是一般neural network的四倍。这个跟Recurrent Neural Network 的关系是什么，这个看起来好像不一样，所以我们要画另外一张图来表示。

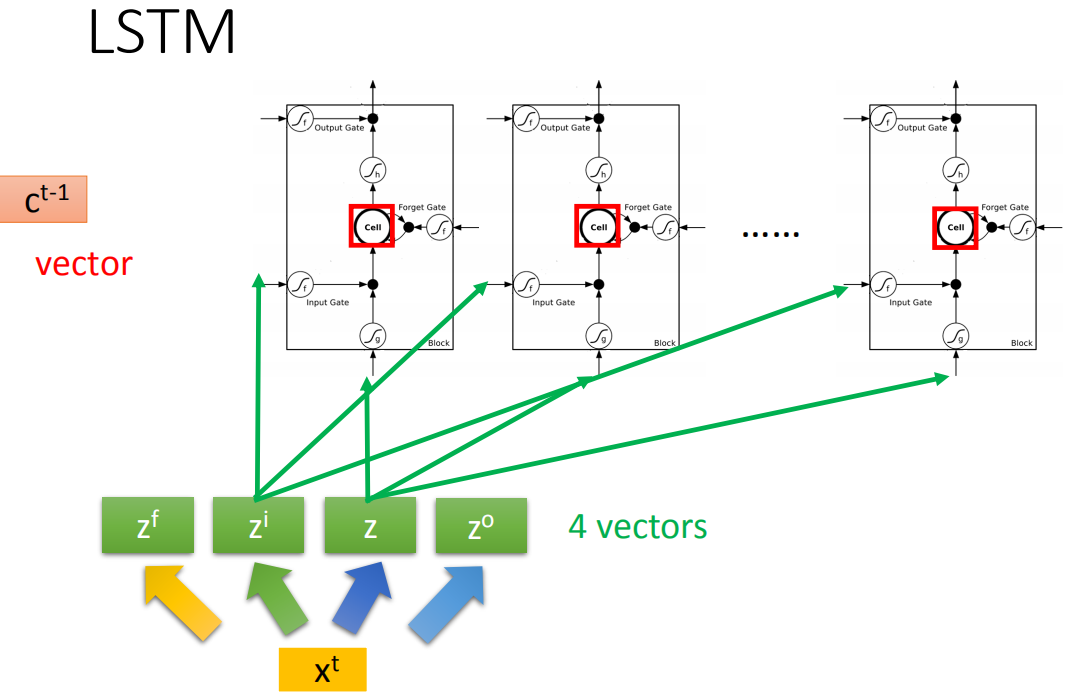
假设我们现在有一整排的neuron(LSTM)，这些LSTM里面的memory都存了一个值，把所有的值接起来就变成了vector，写为 $c^{t-1}$(一个值就代表一个dimension)。现在在时间点t，input一个vector$x^t$，这个vector首先会乘上一matrix(一个linear transform变成一个vector z,z这个vector的dimension就代表了操控每一个LSTM的input(z这个dimension正好就是LSTM memory cell的数目)。z的第一维就丢给第一个cell(以此类推)

这个$x^t$ 乘上另外的一个transform得到$z^i$，然后这个$z^i$ dimension也跟cell的数目一样，$z^i$ 每一个dimension都会去操控input gate(forget gate 跟output gate也都是一样，这里就不在赘述)。所以我们把$x^t$ 以四个不同的transform得到四个不同的vector，四个vector的dimension跟cell的数目一样，这四个vector合起来就会去操控这些memory cell运作。

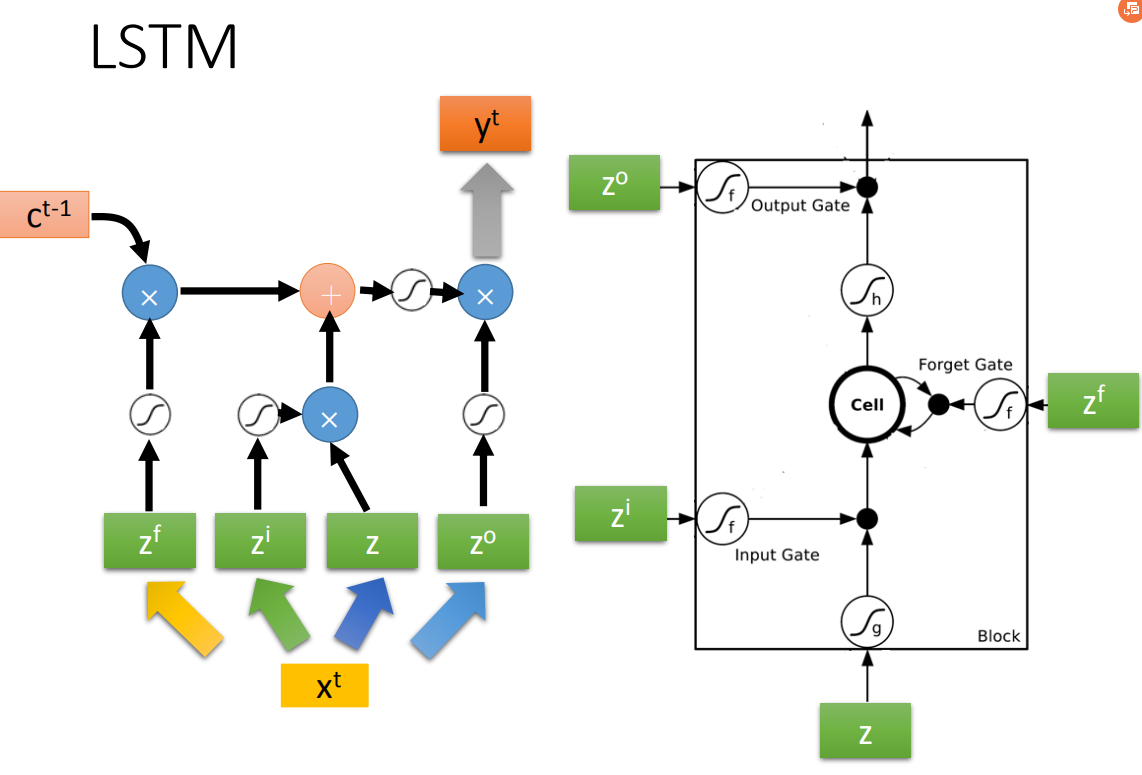一个memory cell就长这样，现在input分别就是$z$,$z^i$,$z^o$,$z^f$(都是vector)，丢到cell里面的值其实是vector的一个dimension，因为每一个cell input的dimension都是不一样的，所以每一个cell input的值都会是不一样。所以cell是可以共同一起被运算的,怎么共同一起被运算呢？我们说，$z^i$ 过activation function跟z相乘，$z^f$ 过activation function跟之前存在cell里面的值相乘，然后将$z$ $z^i$ 乘的值加上$z^f$ $c^{t-1}$ 乘的值，$z^o$ 过activation function的结果output，跟之前相加的结果再相乘，最后就得到了output$y^t$

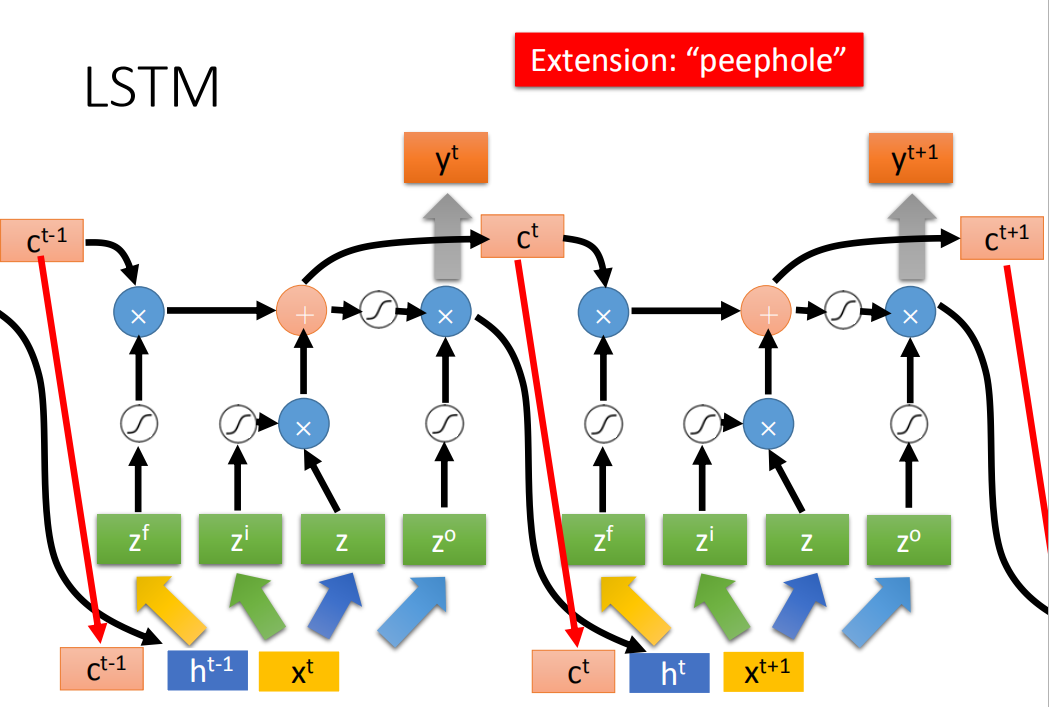之前那个相加以后的结果就是memory里面存放的值$c^t$，这个process反复的进行，在下一个时间点input$x^{t+1}$，把z跟input gate相乘，把forget gate跟存在memory里面的值相乘，然后将前面两个值再相加起来，在乘上output gate的值，然后得到下一个时间点的输出$y^{t+1}$

你可能认为说这很复杂了，但是这不是LSTM的最终形态，真正的LSTM,会把上一个时间的输出接进来，当做下一个时间的input，也就说下一个时间点操控这些gate的值不是只看那个时间点的input$x^t$，还看前一个时间点的output$h^t$。其实还不止这样，还会加一个东西叫做“peephole”，这个peephole就是把存在memory cell里面的值也拉过来。那操控LSTM四个gate的时候，你是同时考虑了$x^{t+1},h^t,c^t$，你把这三个vector并在一起乘上不同的transform得到四个不同的vector再去操控LSTM。

LSTM通常不会只有一层，若有五六层的话。大概是这个样子。每一个第一次看这个的人，反映都会很难受。现在还是 quite standard now，当有一个人说我用RNN做了什么，你不要去问他为什么不用LSTM,因为他其实就是用了LSTM。现在当你说，你在做RNN的时候，其实你指的就用LSTM。Keras支持三种RNN：‘’LSTM‘’,“GRU”,"SimpleRNN"

GRU

GRU是LSTM稍微简化的版本，它只有两个gate，虽然少了一个gate，但是performance跟LSTM差不多(少了1/3的参数，也是比较不容易overfitting)。如果你要用这堂课最开始讲的那种RNN，你要说是simple RNN才行。

GRU是LSTM稍微简化的版本，它只有两个gate，虽然少了一个gate，但是performance跟LSTM差不多(少了1/3的参数，也是比较不容易overfitting)。如果你要用这堂课最开始讲的那种RNN，你要说是simple RNN才行。