ADC

0. 摘要

持续学习方法通常面临灾难性遗忘的问题，尤其是在不存储先前任务样本的方法中，这一问题尤为严重。为了减少特征提取器的潜在漂移，现有的无样本方法通常在第一个任务显著大于后续任务的情况下进行评估。然而，在更具挑战性的设置中，尤其是在第一个任务较小的情况下，这些方法的性能会大幅下降。为了解决无样本方法中的特征漂移估计问题，我们提出通过对当前样本进行对抗性扰动，使其嵌入在旧模型嵌入空间中接近旧类原型。然后，我们利用这些扰动图像估计从旧模型到新模型的嵌入空间漂移，并相应地补偿原型。我们利用了对抗样本在持续学习设置中从旧特征空间到新特征空间的可迁移性。这些图像的生成简单且计算成本低。实验表明，所提出的方法能更好地跟踪嵌入空间中原型的移动，并在多个标准持续学习基准数据集和细粒度数据集上优于现有方法。代码可在 https://github.com/dipamgoswami/ADC 获取。

1. 引言

深度学习在各种计算机视觉任务中得到了广泛应用，展示了在单次训练数据集上的卓越性能。然而，当数据以增量方式引入时，神经网络需要在适应新数据的同时不遗忘先前学习的信息，这种现象被称为灾难性遗忘 [18, 30]。最近的持续学习（CL）研究 [4, 29, 52, 58] 主要关注两种常见场景 [48]：任务增量学习（TIL），其中测试时任务信息可用；类增量学习（CIL），其中任务信息不可用。我们的工作旨在解决更具挑战性的 CIL 问题。

基于样本的 CIL 方法 [2, 3, 6, 8, 13, 25, 38, 50] 存储每个任务的小部分数据。这些样本在训练新任务时与当前数据一起回放。虽然这些方法有效，但它们需要存储先前任务的输入数据，这在实际应用中带来了多重挑战，例如法律问题（如欧洲 GDPR，用户可以请求删除个人数据）以及处理敏感数据（如医学影像）时的隐私问题。最近，无样本 CIL（EFCIL）设置得到了广泛研究 [11, 28, 35, 56, 59–61]。然而，与基于样本的方法不同，EFCIL 方法仅在从高质量特征表示开始时有效，因此依赖于较大的初始任务，通常占整个数据集的一半。然而，更实用的 CIL 方法应能够在较小的初始任务上表现良好，同时不存储样本。我们将其定义为小初始设置，并分析现有 EFCIL 方法在这种设置中的表现。

CIL 中的一个关键方面是在新任务训练后特征表示的语义漂移 [56]。这导致特征空间中类分布的变化。因此，在学习新任务后跟踪旧类表示至关重要。虽然可以使用最近均值样本（NME）[8, 36] 有效估计新特征空间中的类均值，但在没有样本的情况下估计这一漂移具有挑战性。通常，这种漂移通过强功能正则化来最小化，但这限制了网络的可塑性。另一种方法是从当前数据的漂移中估计，如 SDC [56] 所做的那样，或通过使用新类特征增强旧原型 [28, 42]。在本文中，我们提出了一种新的漂移估计方法，使用对抗样本来在新特征空间中复活旧类原型，如图 1 所示。

对抗样本 [1, 14, 27, 31, 46] 是恶意设计的输入，旨在欺骗神经网络预测与原始输入不同的输出。利用目标对抗攻击 [22, 27] 的概念，我们提出扰动新数据，使得对抗图像的嵌入接近旧原型。然后，使用这些对抗样本估计从旧特征空间到新特征空间的漂移，这些样本作为旧类的伪样本。我们假设伪样本在特征空间中表现得像原始样本，因此我们利用它们来测量漂移。与数据反演方法 [55] 相比，生成这些对抗样本的计算成本更低且速度更快（仅需几次迭代）。

根据最近的研究 [11, 16, 26]，我们探索了使用类原型与 NCM [36] 分类器，并展示了在 NCM 分类器的基础上使用 logits 蒸馏的简单基线在小初始设置中通常优于现有的 EFCIL 方法。将我们提出的漂移补偿方法应用于该基线后，我们在使用 CIFAR-100 [20]、Tiny-ImageNet [23] 和 ImageNet-Subset [5] 的标准 CL 基准以及 CUB-200 [49] 和 Stanford Cars [19] 等细粒度数据集上获得了最先进的性能，显著优于现有方法。

我们的贡献可以总结如下：

我们研究了具有挑战性的 EFCIL 设置，并强调了从小初始设置中进行持续学习的重要性，而不是假设第一个任务中有一半的数据集可用。
我们提出了一种新颖且直观的方法——对抗漂移补偿（ADC），用于估计语义漂移并在新特征空间中复活旧类原型。我们还研究了对抗生成的样本在 CIL 设置中从旧模型到新模型的可迁移性。
我们在多个 CIL 基准上进行了实验，并在多个基准数据集上大幅优于最先进的方法。特别是在细粒度数据集上，我们在最后一个任务的准确率上取得了约 9% 的提升。

2. 相关工作

类增量学习。CIL [4, 29, 58] 方法旨在增量学习新数据，并面临灾难性遗忘问题 [30, 37]。在 CIL 评估中，由于没有任务 ID，难以区分属于不同任务的类 [45]。虽然通常使用回放方法 [2, 6, 8, 13, 38] 通过存储原始输入来解决这一问题，但也有一些尝试在不存储原始输入的情况下进行。LwF [24] 通过防止当前模型的输出与先前模型的输出偏离过多来防止网络中的重要变化。PASS [59] 使用自监督学习学习骨干网络，然后使用功能正则化和特征回放，SSRE [60] 提出了一种旨在跨任务传递不变知识的架构组织策略。在 FeTRIL [35] 中，作者冻结了特征提取器，并使用当前任务数据方差估计旧类特征的位置。最近，FeCAM [11] 利用先前任务特征的均值和协方差，提出了一种基于马氏距离的分类器。

漂移估计。在更新新类别的特征提取器时，旧类原型的表示会发生变化，因此需要纠正这些漂移 [56]。SDC [56] 表明，新数据可用于估计旧原型表示的漂移。最近的方法 [28, 42, 47] 也探索了如何更新旧任务中学习的原型以对抗漂移。Toldo 等人提出通过学习旧类和新类特征之间的关系来估计漂移。NAPA-VQ [28] 提出使用特征空间中类的拓扑信息来增强原型。原型回忆 [42] 提出通过将旧原型与新样本特征插值来动态重塑旧类特征分布。在本研究中，我们生成作为伪样本的对抗样本，然后用于测量漂移。

使用对抗攻击的持续学习。近年来，对抗攻击得到了深入研究 [1, 14, 46]，并随后被用于从训练好的视觉模型中生成逼真的图像 [33]，包括可用于训练的输入 [55]。一些最近的基于样本的 CIL 方法 [9, 17, 21, 43] 借鉴了对抗攻击的思想。ASER [43] 使用 kNN 特定的 Shapley 值来获得更具代表性的缓冲区样本。GMED [17] 通过在训练新数据时监控损失的变化来编辑样本。RAR [21] 使用样本与新样本之间的成对关系，并通过扰动样本来获得接近决策边界的样本。虽然这些方法都在记忆样本上使用了对抗攻击，但我们使用它来扰动新数据以模拟旧数据。

3. 方法

我们考虑 EFCIL 设置，其中新类随着时间的推移出现，并且不允许存储旧类的样本。这些类以不同的任务出现，一次一个任务，任务中包含一组互斥的类。在训练任务 $t$ 时，我们可以访问当前数据集 $D_{t} = {X_{t}, Y_{t}}$ ，其中 $X_{t}$ 是图像， $Y_{t}$ 是标签。EFCIL 的主要目标是学习一个模型 $h$ ，能够正确分类迄今为止遇到的所有类。我们使用 $h_{t} (x) = σ (W_{t} f_{t} (x))$ ，其中 $f_{t}$ 是由任务 $t$ 中学习的参数 $θ_{t}$ 参数化的特征提取器， $W_{t}$ 是线性分类器的权重矩阵， $σ$ 是 softmax 函数。

3.1 动机

通常情况下，对于在新数据上训练的新特征提取器 $f_{t}$ 和来自先前任务的旧特征提取器 $f_{t - 1}$ ，我们可以访问到任务 $t - 1$ 为止的旧类原型，记为 $P_{t - 1}^{Y_{1 : t - 1}}$ 。我们在当前任务训练后计算所有新类的原型。对于任务 $t$ 中的类 $k$ ，我们计算 $P_{t}^{k} = \frac{1}{| X_{t}^{k} |} \sum_{x \in X_{t}^{k}} f_{t} (x)$ ，其中 $X_{t}^{k}$ 是来自类 $k$ 的样本集， $f_{t} (x)$ 是来自类 $k$ 的图像 $x$ 的特征嵌入。然而，旧类原型是在旧任务中的旧特征空间 $f_{t^{'}} (t^{'} < t)$ 中计算的，并且在新数据训练后已经漂移到新特征空间 $f_{t}$ 中的不同位置。

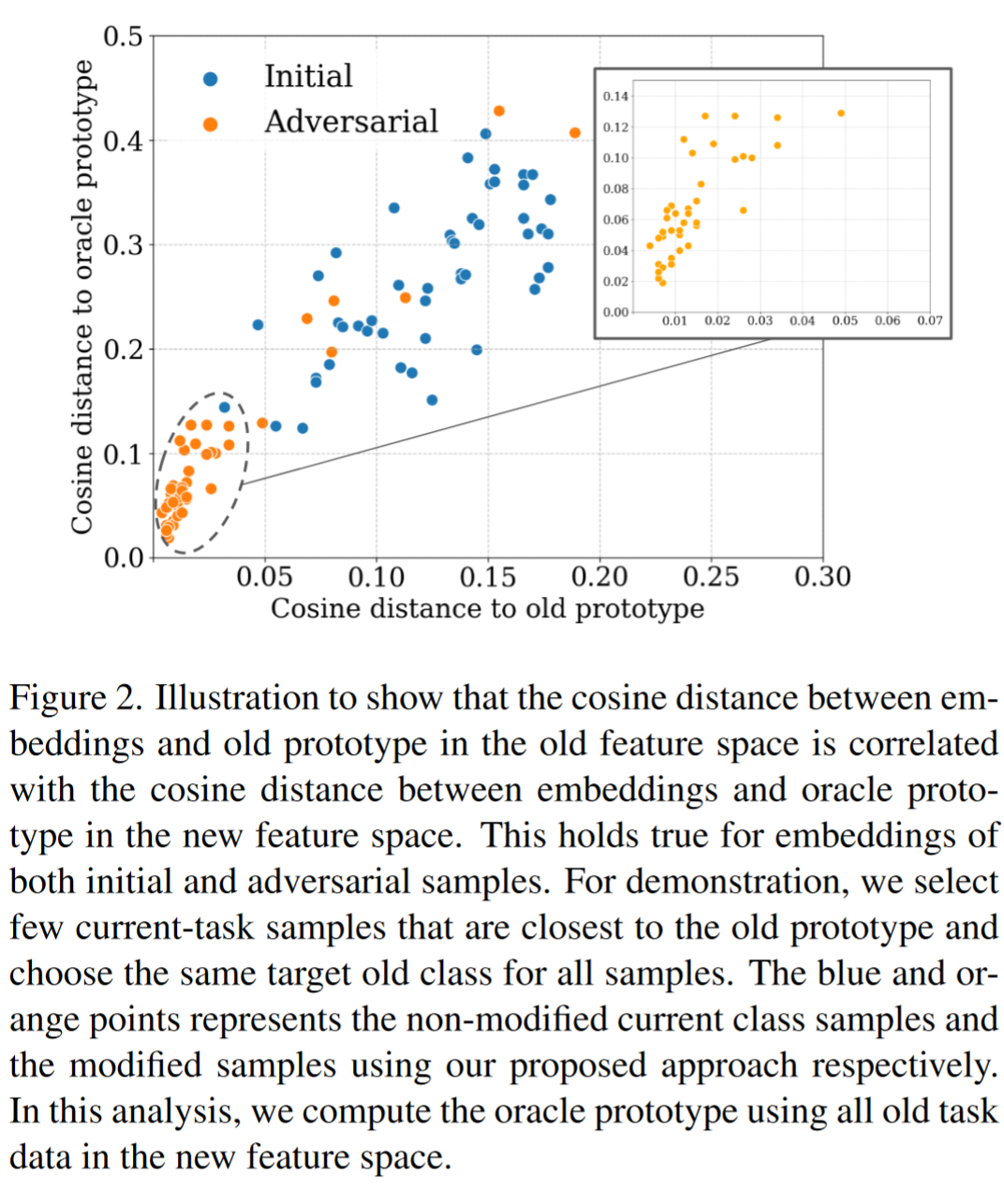
之前，SDC [56] 提出通过计算从旧模型嵌入 $f_{t - 1} (x)$ 到新模型嵌入 $f_{t} (x)$ 的漂移来补偿这些原型 $P_{t - 1}^{Y_{1 : t - 1}}$ 的漂移，其中 $x$ 是当前任务中的所有图像。然后，通过考虑围绕原型的加权高斯窗口（给予靠近原型的漂移向量更多权重），使用当前数据的漂移来近似先前任务原型的漂移。然而，当当前任务数据点中很少有接近给定原型的点时，这种对先前原型漂移的近似质量预计会较低。我们在实验中表明，SDC 在small-start设置中确实难以估计漂移，其中特征表示发生了显著变化。

以类似的方式，可以通过简单地选择每个旧类原型的最接近样本，并在这些样本通过新骨干网络时计算其平均特征，来估计这种漂移，而不需要使用此类权重。我们选择当前任务中接近给定类旧原型的样本，并验证这些样本在新特征空间中也接近 Oracle 原型（见图 2）。我们分析发现，旧特征空间中与旧原型的距离与新特征空间中与 Oracle 原型的距离之间存在相关性（见蓝点）。这促使我们利用当前任务样本，使得它们在旧特征空间中与旧原型的距离更小，从而可能改善漂移估计。我们假设这可以通过从当前任务样本中计算对抗样本来实现，目标是使它们的表示与旧特征空间中的一个旧类原型匹配。

3.2 对抗漂移估计

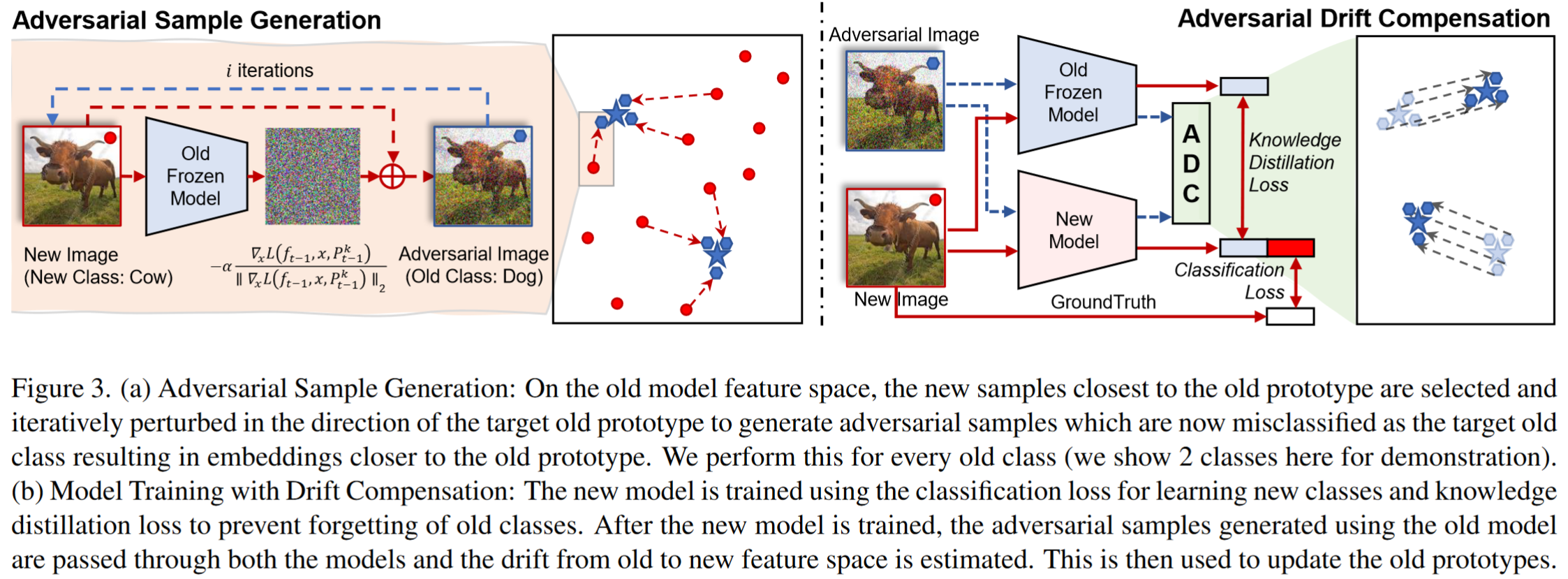
为了估计在更新新类模型后旧类原型的漂移，最好能够访问样本。这些样本可以通过新模型来计算 Oracle 原型在新特征空间中的位置。然而，在无样本设置中，我们只能访问新数据。为了使用新数据来表示旧数据，我们利用了目标对抗攻击 [22, 27] 的概念，一次针对一个旧类，并扰动新数据，使其作为旧数据的替代。我们对新数据进行对抗攻击，使其嵌入在旧特征空间中非常接近旧原型。使用这些对抗样本，我们可以估计从旧特征空间到新特征空间的漂移，并进行补偿，如图 3 所示。

为了估计目标旧类 $k$ 的原型 $P_{t - 1}^{k}$ 的漂移，我们从当前任务数据 $X_{t}$ 中采样一组 $m$ 个数据点 $X^{k}$ ，这些数据点在 $X_{t}$ 中样本的嵌入与原型 $P_{t - 1}^{k}$ 之间的 L2 距离最近。我们的目标是扰动样本 $x \in X^{k}$ ，并获得 $X_{a d v}^{k}$ ，使得对抗样本 $x_{a d v} \in X_{a d v}^{k}$ 更接近 $P_{t - 1}^{k}$ ，并且现在在旧特征空间中使用 NCM 分类器将其分类为类 $k$ ：

\begin{matrix} (1) & k = \arg min_{y \in Y_{1 : t - 1}} ∥ f_{t - 1} (x_{a d v}) - P_{t - 1}^{y} ∥_{2} . \end{matrix}

我们提出以下优化目标，通过计算特征 $f_{t - 1} (x)$ 与原型 $P_{t - 1}^{k}$ 之间的均方误差：

\begin{matrix} (2) & L (f_{t - 1}, X^{k}, P_{t - 1}^{k}) = \frac{1}{| X^{k} |} \sum_{x \in X^{k}} ∥ f_{t - 1} (x) - P_{t - 1}^{k} ∥_{2}^{2} . \end{matrix}

为了将特征嵌入向目标原型 $P_{t - 1}^{k}$ 方向移动，我们计算损失相对于数据 $x \in X^{k}$ 的梯度，归一化以获得单位攻击向量，并按 $α$ 缩放：

\begin{matrix} (3) & x_{a d v} \leftarrow x - α \frac{\nabla_{x} L (f_{t - 1}, x, P_{t - 1}^{k})}{∥ \nabla_{x} L (f_{t - 1}, x, P_{t - 1}^{k}) ∥_{2}} \forall x \in X^{k}, \end{matrix}

其中 $\nabla_{x} L (f_{t - 1}, x, P_{t - 1}^{k})$ 是目标函数相对于数据 $x$ 的梯度， $α$ 是步长。我们进行 $i$ 次迭代的攻击。

这里的目标与传统的对抗攻击（如 FGSM 及其变体 [7, 10, 22, 27]）不同，后者旨在最小化扰动以保持扰动图像在视觉上与真实图像相似，通常基于扰动的 $ℓ_{2}$ 或 $ℓ_{\infty}$ 范数。在我们的情况下，我们不需要对初始图像和最终图像之间的距离施加此类限制，而是仅将扰动图像裁剪到现有像素值范围内。我们在补充材料中展示了生成的对抗图像确实具有更高的扰动。我们还观察到，我们的公式更接近于基于 $ℓ_{2}$ 范数的攻击，因为我们使用梯度的 $ℓ_{2}$ 归一化来获得单位扰动向量，并通过步长进行缩放。

3.3 持续对抗可迁移性

我们的方法的一个有趣之处在于，对抗样本 $x_{a d v}$ 是在旧特征提取器 $f_{t - 1}$ 上生成的，然后传递到新特征提取器 $f_{t}$ ，期望对抗样本仍然被错误分类为目标旧类 $k$ 。我们将此定义为持续对抗可迁移性，即在旧特征空间生成的对抗样本在新特征空间中仍然表现出相同的行为。这是可行的，因为旧模型和新模型并非完全不同，这是由于知识蒸馏用于减少灾难性遗忘。这与对抗可迁移性 [15, 27, 32, 34] 的概念相关，其中在一个神经网络上获得的攻击在其他独立训练的神经网络架构上也表现为攻击。

我们使用旧类数据分析了 Oracle 设置，以验证持续对抗可迁移性。我们在图 2 中展示了对抗样本在旧特征空间中与其目标原型的距离仍然与新特征空间中目标类的 Oracle 原型的距离相关。这表明使用旧特征空间生成的对抗样本在新特征空间中仍然有效，因此允许我们可靠地从这些对抗样本中计算漂移。

3.4 漂移补偿

当对抗样本通过新特征提取器 $f_{t}$ 时，预计它们会接近漂移后的原型，因此用于计算漂移。在为每个目标类 $k$ 生成对抗样本后，我们测量原型漂移为：

\begin{matrix} (4) & Δ_{t - 1 \to t}^{k} = \frac{1}{| X_{a d v}^{k} |} \sum_{x_{a d v} \in X_{a d v}^{k}} (f_{t} (x_{a d v}) - f_{t - 1} (x_{a d v})), \end{matrix}

其中 $x_{a d v} \in X_{a d v}^{k}$ 是仅那些使用 NCM 分类器被分类为目标类 $k$ 的对抗样本集。我们通过补偿漂移来复活旧原型：

\begin{matrix} (5) & P_{t}^{k} = P_{t - 1}^{k} + Δ_{t - 1 \to t}^{k} . \end{matrix}

在补偿所有旧原型后，我们在新特征空间中使用 NCM 分类器对测试样本进行分类。与 SDC [56] 不同，我们不执行基于与原型距离的加权平均，因为对抗图像的嵌入非常接近原型，我们发现应用这种额外的加权方案没有增益。

3.5 训练策略

除了学习新类外，我们还对 logits 进行知识蒸馏 [24]，以将知识从先前任务 $t - 1$ 的冻结教师模型传递到当前任务 $t$ 的学生模型：

\begin{matrix} (6) & L = L_{c e} (h_{t} (x), y) + λ L_{c e} (h_{t - 1} (x), h_{t} (x)), \end{matrix}

其中 $λ$ 是正则化强度，第一项 $L_{c e}$ 是用于学习新类的交叉熵损失，第二项通过强制旧模型 $h_{t - 1}$ 和新模型 $h_{t}$ 对旧类的概率相似来进行正则化，从而防止遗忘。

4. 实验

4.1 数据集

我们在多个 CIL 基准数据集上进行了实验。CIFAR-100 [20] 包含 50k 张 32x32 的训练图像和 10k 张测试图像，分为 100 个类。TinyImageNet [23] 包含 100k 张训练图像和 10k 张测试图像，来自 200 个类，图像大小为 64x64，取自 ImageNet [5] 的子集。ImageNet-Subset 是 ImageNet (ILSVRC 2012) 数据集 [39] 的子集，包含 100 个类，总共 130k 张训练图像和 5k 张测试图像，图像大小为 224x224。我们将所有这些数据集均匀地分为 5 个和 10 个任务。这与 EFCIL 基准 [11, 35, 59] 中常用的第一个任务占数据集一半的大初始设置不同。我们还使用了两个细粒度数据集进行实验。CUB-200 [49] 包含 200 种鸟类，图像大小为 224x224，训练集有 5994 张图像，测试集有 5794 张图像。我们对 CUB-200 使用 5 分割和 10 分割设置。Stanford Cars [19] 包含 196 种汽车模型，图像大小为 224x224，训练集有 8144 张图像，测试集有 8041 张图像，我们将其分为 7 个和 14 个任务。

4.2 训练细节

我们使用 PyCIL 框架 [57] 作为所有实验的基础。训练使用 ResNet18 模型 [12] 和 SGD 优化器进行。对于 CIFAR-100，在第一个任务中，我们使用初始学习率为 0.1，动量为 0.9，批量大小为 128，权重衰减为 5e-4，训练 200 个 epoch，学习率在 60、120 和 160 个 epoch 后分别降低 10 倍。在后续任务中，我们使用初始学习率为 0.05，在 45 和 90 个 epoch 后降低 10 倍，并训练 100 个 epoch。根据 [29]，我们将正则化强度设置为 10，温度设置为 2。网络在 CIFAR-100、TinyImageNet 和 ImageNet-Subset 上从头开始训练。对于细粒度数据集的实验，我们遵循标准实践 [40, 56] 使用 ImageNet 预训练权重。对于 ADC，我们使用 $α = 25$ ，迭代次数 $i = 3$ ，最近样本数 $m = 100$ 作为所有数据集的参数。与大多数现有方法类似，我们存储所有类原型。所有数据集的完整训练设置细节可在补充材料中找到。

4.3 对比方法

由于现有的 EFCIL 方法并非为小初始设置设计，我们在小初始设置中实现了这些方法，包括 LwF [24]、PASS [59]、SSRE [60]、FeTRIL [35] 和 FeCAM [11]。自然，我们还与现有的漂移估计方法 SDC [56] 和使用 NCM 分类器的基线模型进行了比较。对于表 1 和表 2 中报告的 SDC 和 NCM 结果，我们使用 LwF 训练模型，并在特征空间中进行 NCM 分类。对于 FeTrIL 和 FeCAM，特征提取器在第一个任务后被冻结，而对于其他方法，它是持续学习的。请注意，这里我们使用 logits 蒸馏的 SDC 与 [56] 不同，后者在特征上执行蒸馏。

4.4 评估

我们报告了最后一个任务后的平均准确率，记为 $A_{last}$ ，以及增量平均准确率，即所有任务（包括第一个任务）后的准确率平均值，记为 $A_{inc}$ 。 $A_{inc}$ 更好地反映了方法在所有任务中的表现。

5. 实验分析

5.1 定量评估

我们观察到，针对 EFCIL 大初始设置提出的方法在小初始设置中效果不佳，表现较差。使用 LwF 训练并使用 NCM 分类器的简单基线在多个设置中优于大多数现有方法——SSRE、PASS、FeTrIL 和 FeCAM。虽然 SDC 优于 NCM，但提出的方法 ADC 在所有设置中的最后一个任务准确率和增量平均准确率上均优于现有方法（见表 1 和表 2）。ADC 在 CIFAR-100 的 5 任务和 10 任务设置中分别比第二好的方法 SDC 高出 4.2% 和 5.12%。对于 TinyImageNet，ADC 在 5 任务和 10 任务设置中分别比第二好的方法高出 0.95% 和 5.17%。在 ImageNet-Subset 上，ADC 在 5 任务和 10 任务设置中分别比最后一个任务后的第二好的方法高出 2.58% 和 1.72%。

我们还评估了 EFCIL 方法在具有挑战性的细粒度数据集 CUB-200 和 Stanford Cars 上的表现。我们在表 2 中观察到，LwF 在这些数据集上是一个强基线，特别是在 5 任务和 7 任务设置中，而 NCM 和 SDC 等方法并不比 LwF 好很多。虽然 PASS 在两个数据集上表现不佳，但 FeTrIL 和 FeCAM 表现较好，FeCAM 在 CUB-200 的 10 任务设置和 Stanford Cars 的 14 任务设置中优于其他方法。ADC 在 CUB-200 的 5 任务和 10 任务设置中分别比第二名方法高出 5.78% 和 6.19%。在 Stanford Cars 数据集上，ADC 在 7 任务和 14 任务设置中分别比第二名方法高出 9.68% 和 7.57%。我们分析了所有方法在每个任务后的准确率变化（见图 5），观察到 ADC 在所有任务中始终优于其他方法。

5.2 ADC 的计算开销

使用 ADC 需要在每个训练会话之间进行一些额外的计算。在本节中，我们提供了我们方法所需的额外计算量的估计，并将其与单个任务的训练时间进行比较。在每个任务结束时，我们的方法需要估计每个存储原型的漂移（每个旧类一个），并针对每个原型从当前任务样本中计算多个对抗样本。因此，我们的方法的训练时间与类别数量成线性比例。对于每个类，我们在一批中计算 100 个对抗样本，并执行 3 次训练迭代。为了执行一次迭代，我们需要计算对抗损失相对于输入图像的梯度，其成本相当于一次正常的训练反向传播 [41]。因此，如果我们用 $N_{c}$ 表示类别数量，用 $N_{i}$ 表示迭代次数，我们需要执行 $N_{c} \times N_{i}$ 次反向传播。在 CIFAR-100 和 ImageNet-Subset 的 10 任务设置中，每个任务包含 10 个类，这意味着总共需要执行 $\sum_{t = 1}^{9} 10 \times t \times 3 = 1350$ 次反向传播。相比之下，一个新任务训练 100 个 epoch，批量大小为 128（CIFAR-100 的 10 任务设置下每 epoch 有 39 个批次），这意味着每个任务需要执行 3900 次反向传播，第一个任务则需要两倍的计算量（训练 200 个 epoch）。总的来说，我们的方法在该设置下增加了 3.1% 的计算成本。对于 CIFAR-100 和 ImageNet-Subset 的 5 任务设置，计算成本增加了 2.5%。

5.3 消融实验

在 4.3 节中，我们对 ADC 的各种超参数进行了分析，包括迭代次数、 $α$ 值以及用于 ADC 的最近样本数，基于 CIFAR-100（T=10）设置。根据表 3a 的观察结果，我们发现即使选择非常低的迭代次数（特别是 3 次），在生成扰动图像时也能获得良好的结果。此外，使用 $α = 25$ 在增量和最终任务评估中均能获得较高的准确率（见表 3b）。关于最近样本数的选择，表 3c 显示，当样本数超过 100 时，准确率的提升非常有限。因此，我们选择 100 个最近样本进行实验，这在计算上更便宜且仍能获得非常高的准确率。有趣的是，即使仅使用 25 个最近样本，其准确率也比第二名方法 SDC 高出 2.62%。

5.4 漂移估计质量

我们通过表 1 和表 2 验证了设计的 ADC 方法在所有数据集上的准确率均优于之前的 SDC 方法。作为额外的验证，我们检查了该方法在估计旧原型漂移时是否确实优于 SDC。为此，我们在 CIFAR-100 的 5 任务设置中使用相同的训练检查点，分别应用 SDC 和 ADC，并将估计的漂移与使用旧数据计算的真实漂移进行比较。我们在图 6 中报告了结果，展示了估计漂移质量的分布。每个类估计一个漂移，并计算估计漂移与真实漂移的余弦相似度。我们发现，对于所有训练任务，使用 ADC 估计的漂移质量均优于使用 SDC 估计的漂移。我们观察到，使用 SDC 估计的某些类漂移与真实漂移的余弦相似度为负值。然而，我们也发现，随着训练任务的进行，估计质量略有下降。实际上，随着骨干网络的漂移越来越大，估计实际漂移变得更加困难。我们观察到 ADC 的估计质量下降更为显著，可能是因为 SDC 的相似度在第二个任务后已经围绕一个较低的值（0.15）分布，而 ADC 的漂移估计最初围绕 0.9 分布，随后下降并达到最低平均值 0.7。这验证了 ADC 能够有效跟踪特征空间中原型的移动。

6. 结论

在本研究中，我们探索了一种用于无样本持续学习的漂移补偿方法。受对抗攻击技术的启发，我们提出了一种新颖的方法——对抗漂移补偿（ADC）。该方法通过从新任务数据中生成对抗样本，使其嵌入接近旧原型，从而更准确地估计旧原型在类增量学习中的漂移，而无需任何样本。此外，我们分析了持续对抗可迁移性，揭示了一个有趣的观察结果：在旧特征空间（先前任务）中生成的样本在新特征空间（当前任务）中仍然表现出相似的行为。这解释了为什么对抗漂移补偿方法表现优异。通过一系列实验，我们证明了 ADC 能够有效跟踪嵌入空间中的类分布漂移，在多个标准基准上超越了现有的无样本类增量学习方法。重要的是，这些改进是在不增加大量计算开销或内存占用的情况下实现的。

局限性

ADC 方法在设计上需要访问任务边界以触发旧原型漂移的计算，并且需要访问足够数量的当前数据。例如，该方法在在线持续学习设置或持续少样本学习设置中更具挑战性，因为在这些设置中只能访问少量当前数据。未来的工作可以探索这些方向。

上次更新: 2025/06/25, 11:25:50

← RKR DYSON→